De middelwaardestelling.

© h.hofstede (h.hofstede@hogeland.nl)

       
Om de middelwaardestelling te kunnen bewijzen hebben we eerst een hulpstellingkje nodig, en dat is de stelling van Rolle.
Die luidt als volgt:
       
Stelling van Rolle:

Als f continu is op [a, b] en f  is ook differentieerbaar op 〈a, b〉
en als bovendien geldt dat f(a) = f(b)

Dan bestaat er een getal c uit [a, b] zodat  f '(c) = 0
       
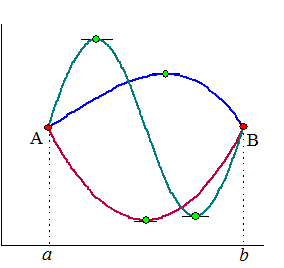
In wat gewoner Nederlands:
"Als je in de figuur hiernaast van punt A naar een even hoog punt B moet gaan zonder je potlood van het papier te halen, dan is op je route ergens de helling nul".

ofwel: wat voor gekleurde grafiek hiernaast je tussen A en B ook verzint, er is altijd minstens één zo'n groen punt te vinden.

Ik hoop dat je snapt dat Rolle hier niet de Nobelprijs voor heeft gekregen.....

Slim voorbeeld. (al zeg ik het zelf)
Toon aan dat  y = 4x5 + x3 + 7x - 2 precies één nulpunt heeft.

Dat gaat zó:

Een beetje proberen geeft al gauw dat f(0) = -2 en f(1) = 10.
Dat betekent (met de tussenwaardestelling) dat ergens tussen 0 en 1 een nulpunt zit, dus er is minstens één nulpunt.
Hoe weten we dat er niet méér dan één nulpunt is?
Kijk naar de afgeleide:  die is gelijk aan  20x4 + 3x2 + 7
Omdat daar alleen maar even machten staan is dat altijd groter dan nul.
Als f nóg ergens een nulpunt zou hebben, dan zegt de stelling van Rolle dat ergens tussen die twee nulpunten de helling gelijk zou zijn aan nul. Maar we zagen net dat dat niet kan omdat die helling altijd groter dan nul is. Dus kan er niet nog een nulpunt zijn.
       
Oké, nu we Rolle onder de knie hebben is het tijd voor de middelwaardestelling:
       
Middelwaardestelling:

Als f continu is op [a, b] en f  is ook differentieerbaar op 〈a, b〉
Dan bestaat er een getal c uit [a, b] zodat:

       
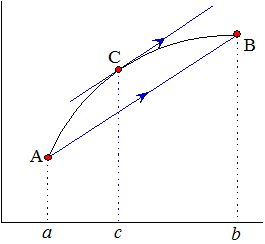
Eerst maar weer "vertalen"?
Zie de figuur hiernaast.
Dat stuk aan de rechterkant van die formule is precies de helling van lijn AB!
Dus er staat hierboven eigenlijk:

"Tussen A en B is altijd een punt C te vinden zodat de raaklijn aan de grafiek in C evenwijdig is aan lijn AB".


 

Voorbeeld.
Een functie f(x) is continu en differentieerbaar op [2,8].
Stel dat f(2) = 12 en stel ook dat we weten dat f '(x) < 4. Wat is de maximale waarde die f(8) kan zijn?

Als je (b - a) van de middelwaardestelling naar links brengt, dan staat er  (b - a) · f '(c) = f(b) - f(a)
Dat geeft  f(b) = f(a) + (b - a) · f '(c)
Invullen:   f(8) = f(2) + (8 - 2) f '(c) = 12 + 6 · f '(c)
Maar omdat f '(c) < 4 is, geeft dat  f(8) < 12 + 6 · 4 = 36.  Dus f(8) is maximaal 36.
       
Geinig gevolg van deze stelling.      
       
Als f overal continu en differentieerbaar is, en f  heeft twee nulpunten, dan volgt daaruit dat f ' minstens één nulpunt heeft.
Kijk maar naar de stelling.
Stel dat die twee nulpunten a en b zijn, dus dat f(a) = f(b) = 0
Dan is de teller van de middelwaardestelling nul, en de noemer niet (b ¹ a), dus is er een c waarvoor die hele breuk nul is, dus waarvoor geldt dat f '(c) = 0.

En op dezelfde manier:  als f  drie nulpunten heeft, dan heeft f 'er minstens twee, dus heeft f '' er minstens één.
Enzovoorts....
       

© h.hofstede (h.hofstede@hogeland.nl)