|
|
 |
|
Twee soorten rijen. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|
Hieronder staan een aantal
"verhaaltjes" waar een rij getallen bij hoort.
Schrijf die rijen getallen op en probeer ze in twee categorieën te
verdelen. Doe dat door van elke rij een recursievergelijking te maken. |
| |
|
|
|
| |
|
|
recursievergelijking: |
| |
a. |
Ik heb een bedrag van
€400,- op een bankrekening staan en krijg
daarover elk jaar 3% rente. |
|
un = 1,04·
un-1 met u0
= 400 |
|
| |
b. |
Je reactievermogen wordt slechter
als je meer glazen alcohol hebt gedronken. In het verkeer is de
reactietijd van een proefpersoon gelijk aan 0,8 seconden. Bij elk
gedronken glas alcohol wordt die tijd 0,2 seconden langer. |
|
un = un-1 + 0,2
met u0 = 0,8 |
|
| |
c. |
Een jongetje heeft met Sint Maarten in totaal
126 snoepjes opgehaald. In de volgende dagen eet hij er daarvan elke dag
7 op. |
|
un = un-1
- 7 met u0 = 126 |
|
| |
d. |
Over het ontstaan van het schaakspel doet het
volgende verhaal de ronde. De uitvinder ervan (Sissa) mocht van zijn
koning als beloning vragen wat hij maar wilde. Hij vroeg één graankorrel
voor het eerste veld van het schaakbord, twéé voor het tweede veld, vier
voor het derde veld, acht voor het vierde veld, enz. Dat leverde hem een
boel graankorrels op! |
|
un = 2 • un - 1
met u1 = 1 |
|
| |
e. |
De eerste keer dat men een oproep om geld te
doneren aan een goed doel uitzendt levert dat 45000 donaties op. Elke
volgende keer wordt dat aantal donaties kleiner omdat het aantal nieuwe
mensen dat bereikt wordt kleiner wordt. Het blijkt dat het aantal
donaties bij elke volgende uitzending steeds ongeveer 10% kleiner wordt. |
|
un = 0,9un -1
met u1 = 5800 |
|
| |
f. |
Bij een sponsorloop krijgt Danieke van haar
buurvrouw
€4,-
en verder voor elk rondje dat ze loopt nog eens €0,15 extra. |
|
un = un - 1 +
0,15 met u0 = 4 |
|
|
g. |
Ik heb een spaarbedrag van
€35000,- in een sok gestopt en die bewaar
ik onder mijn bed. Door de inflatie wordt het bedrag elk jaar 2% minder
waard. |
|
un = un-1•0,98 met
u0 = 35000 |
|
|
|
Welke horen bij elkaar?
Heb je intussen door dat hier twee
verschillende systemen aan 't werk zijn?
a-d-e-g horen bij elkaar, en b-c-f ook......Dat komt
hierdoor: |
| • |
Bij a-d-e-g ziet de
recursievergelijking eruit als un = un-1
+ a (waarbij a eventueel een negatief
getal is).
De regelmaat van deze rijen is, dat de opeenvolgende termen steeds
PLUS hetzelfde getal zijn.
Zo'n rij noemen we een rekenkundige rij. |
| • |
Bij b-c-f ziet de
recursievergelijking er uit als un = un-1
• a.
De regelmaat van deze rijen is, dat de opeenvolgende termen steeds
KEER hetzelfde getal zijn.
Zo'n rij noemen we een meetkundige rij. |
|
|
| Dus: |
|
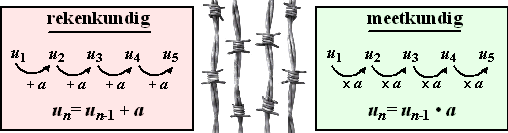 |
|
|
Weet je het nog?
Nou hoop ik dat dit je ergens bekend voorkomt....
Dat je nu een Déja Vu hebt....
Weet je het nog?
We zijn deze twee systemen ("PLUS" en "KEER") namelijk ook al
eerder bij functies tegengekomen. Toen heette het PLUS-systeem "lineair"
(in plaats van rekenkundig) en het KEER-systeem "exponentieel"
(in plaats van meetkundig).
Weet je het nog?
Dat PLUS-getal heette bij lineaire functies het hellinggetal (of ook wel
richtingscoëfficiënt) en dat KEER-getal heette bij exponentiële functies de
groeifactor.
Weet je het nog?
We hadden toen ook formules voor deze twee systemen. De lineaire formule
was y = ax + b en de exponentiële formule was
y = B • gx |
|
|
|
Directe formules voor rijen. |
|
|
Maar toen, vroeger, lang geleden,
toen hadden we nog nooit van rijen gehoord. Toen hadden we geen
recursieformules, maar gewone formules, waar je een x kon
invullen en waar dan een y uitkwam. Omdat een meetkundige en een
rekenkundige rij in feite hetzelfde zijn als een lineair en een
exponentiele functie kunnen we voor dit soort rijen ook de "gewone"
formule van vroeger natuurlijk gebruiken. Daarbij is de x nu
vervangen door een n en de y door een un.
Zo'n "gewone" formule heet bij rijen een directe formule. Het woord zegt
het eigenlijk al: je kunt een un direct uitrekenen als
je n weet, zonder alle vorige un te moeten
berekenen.
Maar er zijn twee belangrijke verschillen:Verschil 1.
Rijen zijn discreet.
Denk er goed om dat de n-waarden alleen gehele getallen kunnen
zijn. 't Zijn immers de nummers?
Dat betekent ook dat een eventuele grafiek er niet uit zal zien als een
kromme, maar als een verzameling losse stippen.
Vergelijk de volgende twee figuren met elkaar: |
| |
|
|
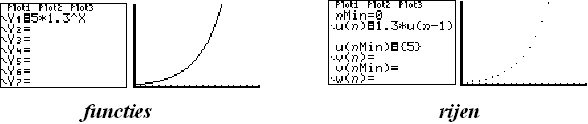 |
|
|
| Verschil 2.
De beginwaarde. |
|
Bij functies was het allemaal
makkelijk: Bij de formules y = ax + b en y = B • gx waren de
constanten b en B de beginwaarden. Dat stelde voor
de y die hoorde bij x = 0 (in de grafiek het
snijpunt met de y-as). Maar we hebben al gezien dat bij rijen de
eerste soms u0 heet en soms u1. Dat
hangt een beetje van het verhaaltje eromheen af. soms is het logischer om
de eerste u0 te noemen en soms is u1
logischer.
Kijk nog maar eens naar de verhaaltjes helemaal bovenaan. Bij twee
daarvan (d en e) vond ik het logischer om de eerste van de rij u1
te noemen. Jij ook????
Als de eerste u0 heet, dan is er niks aan de hand, dan
kun je voor een directe formule gewoon u0 = beginwaarde
= b / B nemen. Maar als de eerste u1
heet, dan moet je uitkijken; kijk maar: |
| |
|
| |
voorbeeld.
Geef een directe formule voor de rij u1 = 3,
u2 = 7, u3 = 11, u4
= 15, ...
Je ziet natuurlijk dat dit een rekenkundige rij is, dus de directe
formule heeft de vorm un = a • n + b.
Daarbij is a het getal dat er steeds bijkomt,
dus in dit geval a = 4. Maar als je nu zonder na te denken
voor het begingetal b = 3 neemt staat er un = 4n
+ 3 en dat klopt niet! Dat zou bijvoorbeeld geven u4
= 4 • 4 + 3 =19 en je ziet in de rij dat u4
gelijk is aan 15.
Er zijn twee mogelijke oplossingen voor dit probleem: |
| |
|
|
| |
| |
Oplossing 1.
Bereken wat u0 zou zijn geweest als hij had
bestaan en neem dat als beginwaarde.
Dat zou in dit geval geven u0 = 3 - 4 = -1 =
b en dus un = 4n
- 1 en die klopt wél. |
| |
|
|
|
| |
Oplossing 2.
Vervang n in de vergelijking door n - 1
Dat zou in dit geval geven un = 4(n
- 1) + 3 en die klopt ook.
(en als de rij bijvoorbeeld was begonnen met u4,
dan vervingen we n door n - 4 natuurlijk...)
|
| |
|
|
|
|
| |
|
|
Samengevat: |
| |
|
| |
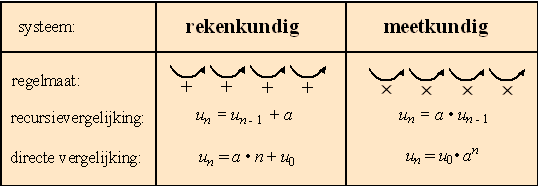 |
| |
|
| |
|
|
OPGAVEN |
| |
|
| 1. |
Geef directe formules voor de voorbeelden a
t.m. g bovenaan deze les. |
| |
|
|
|
|
| 2. |
Geef van de volgende rijen een
directe vergelijking en een recursievergelijking |
| |
|
|
|
|
| |
a. |
12 - 26 - 40
- 54 - 68 - .... |
|
| |
|
|
|
| |
b. |
40 - 60 - 90
- 135 - .... |
|
| |
|
|
|
|
| 3. |
Een octaaf op een piano bestaat uit
12 tonen.
De frequenties van deze tonen vormen een meetkundige rij.
De centrale C van een piano heeft frequentie 256 Hz. De C
die twaalf tonen hoger ligt heeft frequentie 512 Hz. |
 |
| |
|
|
| |
a. |
Stel een directe en een recursieve formule op
voor de frequentie fn van toon nummer n
als de C nummer 1 heeft. |
| |
|
|
| |
b. |
Bereken vervolgens met deze directe formule de
frequentie van de A uit deze toonladder. |
| |
|
|
|
|
| 4. |
Omdat de grote wijzer van een klok
sneller loopt dan de kleine wijzer haalt hij de kleine wijzer af
en toe in.
Op tijdstip t = 0 is het precies 0:00 uur.
De tijdstippen waarop beide wijzers precies op dezelfde plaats
staan vormen een rekenkundige rij met recursieformule
tn = tn-1 +
720/11 waarbij t in minuten is
gegeven. |
 |
| |
|
|
|
| |
a. |
Toon aan dat dat juist is. |
|
| |
|
|
|
| |
b. |
Geef een directe formule voor deze rij |
|
| |
|
|
|
|
| 5. |
Papierformaten zijn niet zomaar
gekozen....
Als je een kopietje op A4-papier wilt vergroten naar A3-formaat,
dan moet dat A3-papier natuurlijk wel dezelfde verhoudingen
hebben als het A4 papier, anders zou de "vorm" van je
plaatje veranderen. |
| |
Verder zijn de
papierformaten zó gekozen dat de lengte van een volgend
formaat steeds gelijk is aan de breedte van de vorige. Hiernaast
zie je hoe een vel A0-papier is onderverdeeld in steeds kleinere
formaten. |
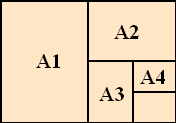 |
| |
|
|
| |
a. |
Als een formaat lengte L en breedte B heeft, dan
heeft het volgende formaat dus lengte B en breedte
1/2L.
Laat zien dat daaruit, en uit de gelijkvormigheid van het
papier, volgt dat de afmetingen van de verschillende formaten een
meetkundige rij vormen met factor √2. |
| |
|
|
|
|
| |
Omdat geldt L = B√2
en omdat A0 papier een oppervlakte van 1 m2 heeft kun
je aantonen dat de afmetingen van A0-papier 1189 bij 841 mm
zijn. |
| |
|
|
|
|
| |
b. |
Geef die afleiding. |
| |
|
|
|
| |
c. |
Geef een directe formule voor de
lengte van An-papier. |
|
| |
|
|
|
|
| |
Ook de oppervlaktes van de
opeenvolgende papiersoorten vormen een meetkundige rij.
Daarvoor geldt natuurlijk On =
1/2
• On-1 met O0 = 1 |
| |
|
|
|
|
| |
d. |
Onderzoek met deze formule en je GR
welk papiernummer voor het eerst een oppervlakte kleiner dan 1
mm2 heeft. |
|
| |
|
|
|
| |
e. |
Geef een directe formule voor On
en controleer daarmee je antwoord op vraag d). |
|
| |
|
|
|
|
| 6. |
Voor een rij getallen geldt dat u4
= 162 en u7 = 4374. |
| |
|
|
|
|
| |
a. |
Bereken u9 als het
een rekenkundige rij is |
|
| |
|
|
|
|
| |
b. |
Bereken u9 als het een
meetkundige rij is. |
|
|
| |
|
|
|
|
 7. 7. |
Drie opeenvolgende
termen van een meetkundige rij hebben som 13/4
en product 1/8. |
| |
|
|
|
| |
a. |
Welke drie termen zijn dat? |
|
| |
|
|
|
| |
b. |
En hoe is dat als de rij rekenkundig
is? |
|
| |
|
|
|
|
| 8. |
De draagtijd van een rat is ongeveer
een maand. Iets minder zelfs, en dat betekent dat een rat
ongeveer elke maand een nest kan krijgen. Zo'n nest bestaat uit
8 - 12 nieuwe ratten, die ook direct zelf weer nakomelingen
kunnen krijgen.
Neem aan dat de helft van de geboren ratten vrouwtjes zijn en de
helft mannetjes. Neem verder aan dat elk vrouwtje inderdaad
iedere maand (behalve de eerste) een nest van precies 10 ratjes
krijgt, en dat er helemaal geen ratten doodgaan. Neem tenslotte
(voor het gemak) aan dat het aantal ratten geen geheel getal
hoeft te zijn.
Stel dat we beginnen met een populatie van 20 vrouwtjesratten en
20 mannetjesratten
Dan vormt het aantal vrouwtjesratten in de loop van de maanden
een meetkundige rij. |
| |
|
|
|
|
| |
a. |
Laat zien dat dat zo is en geef de
reden van die rij. |
| |
|
|
|
|
| |
b. |
Leg uit waarom het totaal aantal
ratten dan ook een meetkundige rij vormt, met dezelfde reden. |
| |
|
|
|
|
| |
Als we de nestgrootte N noemen (in
plaats van 10) en het beginaantal ratten B (helft mannetje,
helft vrouwtjes) dan geldt de formule: At =
B • (1 + 0,5 • N)t met A het
totaal aantal ratten in maand nummer t. |
| |
|
|
|
|
| |
c. |
Toon dat aan. |
|
|
| |
|
|
|
|
| |
Voor een bepaalde rattenkolonie
werden de volgende tellingen gevonden: |
| |
|
|
|
|
| |
| maand |
1 |
2 |
3 |
4 |
| totaal aantal |
60 |
300 |
1500 |
7500 |
|
| |
|
|
|
|
| |
d. |
Bereken de nestgrootte voor deze
kolonie ratten |
| |
|
|
|
|
| 9. |
Gegeven is de rij breuken: 4/9
7/14 10/19
13/24 16/29 ..... |
| |
|
|
|
|
| |
a. |
Geef van zowel de rij getallen in de tellers als die in
de noemers de directe formule.
Noem de eerste uit de rij steeds u1. |
| |
|
|
|
|
| |
b. |
Geef de directe formule van de rij breuken. |
| |
|
|
|
|
| |
c. |
Bij welke grenswaarde komt de rij steeds dichter te
liggen? Vanaf welke n verschilt un minder dan
0,01 van deze grenswaarde? |
| |
|
|
|
|
| |
|
|
|
|
| 10. |
x,
y,
z vormen een
meetkundige rij met reden r
x,
2y,
3z vormen
een rekenkundige rij.
Waaraan is r dan
gelijk? |
| |
|
|
|
|
| |
|
|
|
|
| 11. |
Van een een rekenkundige rij u1 - u2
- ... is bekend dat de eerste drie termen samen gelijk zijn aan 12.
Verder is gegeven dat de u1 - u2
- u6 een meetkundige rijtje is. Bereken
u10 |
| |
|
|
|
|
| |
|
|
|
|
| 12. |
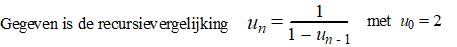 |
| |
|
| |
a. |
Bewijs dat un +
3 = un |
|
|
| |
|
|
|
|
| |
b. |
Bereken u2012 |
|
|
| |
|
|
|
|
| |
|
|
|
|
| 13. |
Gegeven is
de directe vergelijking u(n) = 92-n
• 4n + 1
Toon algebraïsch aan dat dit een meetkundige rij is, en geef de
beginwaarde en de reden. |
| |
|
|
|
|
| 14. |
Vlaamse Olympiade. |
| |
|
|
|
|
| |
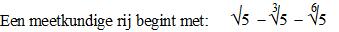 |
| |
Wat is de
volgende term? |
| |
|
|
|
|
| |
|
|
|
 |
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |