|
|
 |
|
Impliciet Differentiëren. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
Differentiëren, dat
ken je natuurlijk nog wel. Toch??
Dat was het opstellen van f ' om de helling van een grafiek
te berekenen.
Maar ja, als je geen formule voor f hebt (zoals bij
impliciete vergelijkingen), dan kun je ook geen formule voor f '
maken...........
Toch willen we graag de helling van een kromme die door een impliciete
vergelijking is gegeven berekenen.
Hij hééft natuurlijk wél een helling!
Hoe achterhalen we die helling?
Daar gaat deze les over. |
| |
|
Neem bijvoorbeeld de kromme:
y2 + 4x = x2 + 2y3 -
6
Het gaat echt niet lukken om die als y = ...
te gaan schrijven, geloof me. |
Maar STEL nou dat we dat wél kunnen...
Stel dat we bijvoorbeeld alles kunnen.. dat we GOD zijn!
(of Allah of zo)
Die kan immers alles?
Dus vast ook wel deze vergelijking schrijven als y = ....
Laten we eens aannemen dat GOD voor ons deze vergelijking heeft
geschreven als y = 2x3
+ 4x
(Dat klopt natuurlijk niet, dat weet ik ook wel, maar neem het
voorlopig even aan).
Als dat zo is, dan kunnen we elke y in de impliciete vergelijking
daar dus door vervangen. Dat geeft:
(2x3 + 4x)2
+ 4x = x2 + 2(2x3
+ 4x)3 -
6 |
 |
| |
|
En nu kun je wél differentiëren.
Met de kettingregel geeft dat vrij eenvoudig:
2 • (2x3 + 4x)
• (6x2 + 4) + 4 =
2x + 6 • (2x3 + 4x)2•
(6x2 + 4)
Daarbij zijn die blauwe stukjes afkomstig van de kettingregel: ze
zijn de afgeleide van y. En die rode stukjes zijn y zelf
natuurlijk, dat had je hopelijk al wel gezien.
Oké, genoeg gedroomd.... We hebben natuurlijk helemaal geen formule
voor y.
Maar wacht eens even..... Ook dán geldt dat verhaal van de rode en die
blauwe stukjes hierboven nog steeds!!!!!
Dan staat daar: 2 • y •
y' + 4 = 2x + 6
• y2
• y'
⇒ 2 • y
• y'
- 6 •
y'•
y2
= 2x - 4
(genoeg met al die kleurtjes)
⇒ y' • (2y
- 6y2) =
2x - 4 |
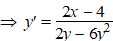 |
|
| |
|
|
En ja hoor! Nou is het tóch
gelukt!! |
| |
|
Als we een punt van de kromme
hebben kunnen we gewoon tóch y' uitrekenen.
Neem bijvoorbeeld het punt (5,1) dat op de kromme ligt. |
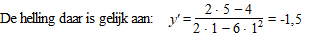 |
| De kromme heeft daar dus helling -11/2. |
|
| |
|
|
Horizontale en Verticale Raaklijnen. |
| |
|
Nu we een manier hebben om de
helling van een kromme te bepalen kunnen we ook uitzoeken waar de kromme
horizontaal loopt en waar verticaal. Immers:
| |
| horizontaal: |
helling = 0 |
0/iets |
| verticaal: |
helling =
∞ |
iets/0 |
|
|
| |
Het eerste geval vinden we als de teller nul is, het tweede als de
noemer nul is (als beide nul zijn?.... daar hebben we het later nog wel
eens over)
In bovenstaand voorbeeld betekent dat, dat de kromme horizontaal is als
2x- 4 = 0 dus bij x = 2.
En de raaklijn is verticaal als 2y - 6y2
= 0, dus bij y = 0 of y =
1/3. |
| |
|
| De
productregel niet vergeten. |
|
| |
|
Nou stonden in het voorbeeld de
x en y mooi gescheiden van elkaar. Natuurlijk kan het ook
gebeuren dat er termen met x én y tegelijk in een
impliciete vergelijking staan. In zo'n geval moet je uiteraard de
productregel gebruiken.
En dan komt daar elke keer bij de afgeleide van y een y'
van de kettingregel.
Een voorbeeld zal het wel duidelijk maken.
Voorbeeld.
Gegeven is de kromme 2y2 + 6xy = 3xy2
+ 9. Geef de vergelijking van de raaklijn in het
punt (1,3)
Differentiëren: 4yy' + 6y + 6xy' =
3y2 + 3x • 2yy'
y'(4y + 6x - 6xy) = 3y2 -
6y |
|
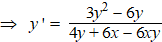 |
|
| In het
punt (1,3) is dus y' = (27
- 18)/(12
+ 6 - 18) = 9/0
dus de raaklijn is verticaal: het is de lijn x = 1.
|
| |
|
| Een
bepaalde helling zoeken. |
|
| |
|
Dat gaat eigenlijk precies als
bij "gewone" functies.
Als je een punt zoekt met helling a dan stel je gewoon y'
gelijk aan a.
Dat levert deze keer niet een x-waarde op, maar meestal een
vergelijking met x en y.
Met deze vergelijking samen met de oorspronkelijke vergelijking van
de kromme moet je maar proberen x en y op te lossen.
Meestal zal dat met substitutie moeten: maak van één
van beide vergelijkingen y =... of x = ... en vul dat in
in de andere.
|
Voorbeeld.
De lijn y = 1,8x + b raakt de kromme xy
= y2 + 1. Bereken b.
Differentiëren: y + xy' = 2yy'
⇒ y'(2y - x)
= y ⇒ y' = y/(2y
- x)
y/(2y - x) = 1,8
⇒ y = 1,8(2y
- x)
⇒ y = 3,6y
- 1,8x
⇒ -2,6y = -1,8x
⇒ x = 14/9y
Invullen in de oorspronkelijke vergelijking:
14/9y
• y = y2 + 1 ⇒
4/9y2
= 1 ⇒ y2 =
9/4
⇒ y = 11/2
∨ y = -11/2
Dat geeft x = 21/6
∨ x = -21/6
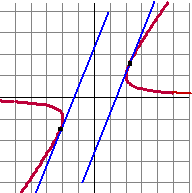
Dat levert tenslotte de lijnen y = 1,8x
- 2,4
en y = 1,8x + 2,4
Hiernaast zie je dat het klopt. |
 |
| |
|
|
Differentialen. |
|
| |
|
Er is nog een andere manier om de
afgeleide van een impliciete vergelijking te noteren, en die manier
vinden de meeste wiskundigen wat mooier, omdat de x en de y
er wat gelijker in behandeld worden. Dat "gelijk behandelen" van x
en y is nou juist wat er bij impliciete vergelijkingen gebeurt.
Dat noteren van de afgeleide gaat met zogenaamde "differentialen" en het
werkt als volgt.
|
| |
Stukje nostalgie:
Toen je voor het eerst met de afgeleide te maken kreeg ging je
die benaderen door een "punt vlak ernaast" te nemen en dan
Δy/Δx
te berekenen. En als je dat punt dan dichter en dichter ernaast
ging kiezen naderde die
Δy/Δx
naar de helling. Dat gaf je dan aan met dy/dx
Die dy en dx zijn dus kleine lijnstukjes
die je zo klein mogelijk wilt maken (maar helemaal nul kan
niet; dan staat er 0/0). Ze heten
differentialen. |
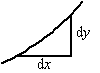 |
|
| |
|
| Bedenk goed dat die dy en
dx beiden oneindig klein zijn en op zichzelf alleen niets
voorstellen. Alleen hun verhouding dy/dx
heeft betekenis. |
| |
Als je nou bij het differentiëren
hierboven die y' schrijft als dy/dx
dan krijg je bij het eerste voorbeeld bovenaan deze les zoiets:
y2 + 4x = x2 + 2y3 -
6
2 • y •
y' + 4 = 2x + 6
• y2
• y'
2y • dy/dx + 4 = 2x
+ 6y2 • dy/dx
En nou komt het: vermenigvuldig alles met dx:
2ydy + 4dx = 2xdx + 6y2dy
Je doet dus alsof die dy en dx wél gewoon een waarde
hebben. Zolang je ze maar beiden in een vergelijking laat staan mag dat
wel, want je kunt dit altijd weer omschrijven naar hun verhouding.
Kijk maar;
2ydy + 4dx = 2xdx + 6y2dy
.....(1)
2ydy - 6y2dy = 2xdx
- 4dx
dy(2y - 6y2) = dx(2x
-
4)
dy/dx = (2x - 4)/(2y
- 6y²)
En daar staat de afgeleide weer!!!!
Die regel nummer (1) hierboven kun je direct uit de vergelijking van de
kromme opschrijven. Als je zo'n gedifferentieerde vergelijking met dx
vermenigvuldigt komt er dus elke keer als je de y differentieerde
nu alleen nog dy bij te staan (en niet meer y ' =
dy/dx), en elke keer
als je de x differentieert komt er dx bij te staan
(daar stond eerst niks).
Mooi symmetrisch toch?
voorbeeld: bereken de helling van de
vergelijking x2 + 2y3 = 4xy
+ 5x - 2
in één keer: 2xdx + 6y2dy
= 4ydx + 4xdy +
5dx
die beide blauwe stukken zijn van de productregel: bij de
eerste is x gedifferentieerd, bij de tweede y.
2xdx - 4ydx
- 5dx = 4xdy
- 6y2dy
dx(2x - 4y
- 5) = dy(4x
- 6y2)
dy/dx = (2x - 4y
- 5)/(4x - 6y²)
En de tweede afgeleide, hoe is
het daarmee? |
| |
|
Het zal je waarschijnlijk
(hopelijk) niet verbazen dat we de tweede afgeleide vinden door de
eerste afgeleide gewoon wéér te differentiëren. Maar dan wel weer
impliciet.
Voorbeeld. Geef de tweede afgeleide (naar
x) van de vergelijking y3 + 2x2
= 6
Eerste afgeleide: 3y2 dy + 4xdx
= 0 ofwel dy/dx =
-4x/3y²
Voor y '' moeten we deze laatste uitdrukking nu weer
differentiëren naar x, maar bedenk daarbij goed dat y een
functie van x is. De quotiëntregel geeft in dit geval: |
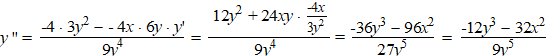 |
| Je ziet dat de y'
weer is vervangen door de eerder gevonden uitdrukking. |
| |
|
|
OPGAVEN |
| |
|
| 1. |
Gegeven is de kromme K: x2y
+ x2 = 6 + 2y2
|
| |
|
|
|
| |
a. |
Geef een vergelijking van de
raaklijn aan K in het punt (√6,
3) |
| |
|
|
|
| |
b. |
In welke punten van K is de raaklijn
evenwijdig aan de y-as? |
| |
|
|
|
| |
|
|
|
| 2. |
Gegeven is de kromme K door:
x2 - 4y2 = 5 |
| |
|
|
|
| |
a. |
Een lijn met r.c. 3/4
raakt kromme K. Geef een vergelijking van deze raaklijn. |
| |
|
|
|
| |
b. |
Onderzoek of K horizontale en/of
verticale raaklijnen heeft. |
| |
|
|
|
| |
c. |
Voor welk a hebben de lijnen
y = ax punten met K gemeen? |
| |
|
|
|
| |
d. |
Leg uit dat y =
1/2x
en y = -1/2x
scheve asymptoten van K zijn. |
| |
|
|
|
| |
|
| 3. |
(examenvraagstuk 1981) |
| |
|
|
|
| |
Gegeven is de kromme K: x3
+ 6xy - 3y2 = 0 |
| |
|
|
|
| |
a. |
Bereken de coördinaten van de punten
van K waar de raaklijn evenwijdig is aan de x-as of de
y-as. |
| |
|
|
|
(-3, -3) en (-22/3, -35/9) |
|
| |
De lijn x = p snijdt K
in de punten A en B.
Er is een negatieve waarde van p waarvoor de lengte van
lijnstuk AB maximaal is |
| |
|
|
|
| |
b. |
Bereken die waarde van p en
de bijbehorende lengte van AB. |
| |
|
|
|
| |
c. |
Voor welke q heeft de lijn
y = qx precies één punt met K gemeen? |
| |
|
|
|
| |
d. |
Teken K en de bij b) en c) behorende
lijnen voor x ∈
[-3, 5] |
| |
|
|
|
| 4. |
Gegeven is de kromme K: x
- ylny = 0
Bereken de coördinaten van de punten van K waarin de raaklijn
evenwijdig is aan de x-as of de y-as. |
| |
|
|
|
| |
|
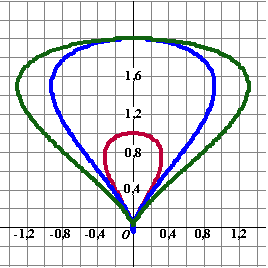
| 5. |
Gegeven is de kromme K:
b2x2 = y3(a
-
y)
Voor verschillende waarden van a en b is hiernaast
drie keer een kromme K getekend. |
 |
| |
|
|
| |
a. |
Bepaal welke waarden van a en b
bij deze krommen horen. |
| |
|
|
| |
b. |
Eén van de krommen K
heeft een verticale raaklijn in het punt (Ö3,6).
Bereken de waarden van a en b voor deze kromme. |
| |
|
|
| |
c. |
De krommen lijken wel wat op
luchtballonnen, vind je niet?
Voor de maximale breedte B van zo'n luchtballon geldt: |
| |
|
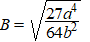 |
| |
|
Toon dat aan. |
| |
|
|
|
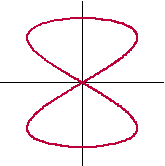
| 6. |
Hiernaast staat de
kromme K getekend die gegeven wordt door:
K: x2 + (y2
- 1)2 = 1 |
 |
| |
|
|
| |
a. |
Bereken de coördinaten van de
punten van K waarin de raaklijn verticaal is. |
| |
|
|
| |
b. |
Een lijn y = p snijdt
de kromme in de punten A en B zodat
AB = √3. Bereken p. |
| |
|
|
| |
|
|
|
| 7. |
examenvraagstuk VWO, 1982. |
| |
|
|
|
| |
Ten opzichte van
een rechthoekig assenstelsel Oxy is gegeven de kromme K met
vergelijking:
x4 - 4x2 + 4y2 = 0 |
| |
|
|
|
| |
a. |
Voor welke p
∈ R heeft de lijn y = px drie
verschillende punten met K gemeen? |
| |
|
|
|
| |
b. |
Bereken de coördinaten van de punten van K waarin de raaklijn aan K
evenwijdig is aan de x-as of aan de y-as. |
| |
|
|
|
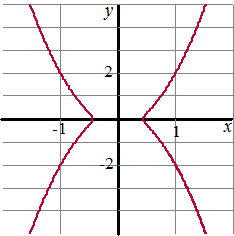
| 8. |
De Kampyle van
Eudoxus.
Ka is de kromme met vergelijking y2
= ax4 - x2
Hiernaast zie je één van de krommen Ka. |
 |
| |
|
|
| |
a. |
Bepaal de waarde van a voor deze kromme. |
| |
|
|
| |
b. |
In welk punten van K1 is de helling
gelijk aan -1? |
| |
|
|
| |
c. |
Leg uit wat er met Ka in de
oorsprong aan de hand is. |
| |
|
|
|
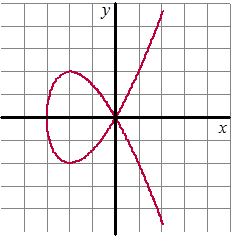
| 9. |
K is de kromme y2
= x3 + 3x2
Zie de figuur hiernaast. |
 |
| |
|
|
| |
a. |
De raaklijnen aan K in de punten
waar x = 6 snijden elkaar in S.
Geef de coördinaten van S. |
| |
|
|
| |
b. |
In welke punten heeft K een
horizontale raaklijn? |
| |
|
|
 |
|
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
 |
| |
|