|
|||||
| 1. | a. | x2y
+ x2 = 6 + 2y2
2xydx + x2dy + 2xdx = 4ydy dx(2xy + 2x) = dy(4y - x2) dy/dx = (2xy + 2x)/(4y - x²) (√6, 3) geeft dan dy/dx = (6√6 + 2√6)/(12 - 6) = 4/3√6 3 = 4/3√6 √6 + b geeft b = -5 de raaklijn is y = 4/3√6 x - 5 |
|||
| b. | dy/dx
= ±∞
als de noemer nul is: 4y - x2 = 0 x2 = 4y invullen: 4y y + 4y = 6 + 2y2 2y2 + 4y - 6 = 0 y2 + 2y - 3 = 0 (y - 1)(y + 3) = 0 y = 1 ∨ y = -3 y = 1 geeft x2 = 4 dus x = 2 x = -2 en de punten (-2, 1) en (2, 1) y = -3 geeft x2 = -12 en dat heeft geen oplossingen |
||||
| 2. | a. |
x2 - 4y2 = 5 2xdx - 8ydy = 0 dy/dx = 2x/8y = x/4y = 3/4 dan is x = 3y (3y)2 - 4y2 = 5 5y2 = 5 y = 1 ∨ y = -1 en dat geeft de punten (3, 1) en (-3, -1) 1 = 3/4 3 + b geeft b = -11/4 en de raaklijn y = 3/4x - 11/4 -1 = 3/4 -3 + b geeft b = 11/4 en de raaklijn y = 3/4x + 11/4. |
|||
| b. | dy/dx
= 0 2x = 0 x = 0 -4y2 = 5 en dat heeft geen oplossingen dy/dx =
±∞
|
||||
| c. | y = ax
invullen:
x2 - 4(ax)2 = 5 x2(1 - 4a2) = 5 x2 = 5/(1 - 4a²) Dat heeft oplossingen als 1 - 4a2 > 0 1 - 4a2 = 0 geeft a = 1/2 a = -1/2 Er zijn punten met K gemeen als -1/2 < a < 1/2 |
||||
| d. | delen door x2:
1 - 4(y/x)2 = 5/x2
Als x naar oneindig gaat, staat er 1 - 4(y/x)2 = 0 (y/x)2 = 1/4 y/x = 1/2 ∨ y/x = -1/2 Dat geeft y = 1/2x ∨ y = -1/2x De kromme nadert naar deze lijnen dus zijn dit scheve asymptoten. |
||||
| 3. | a. | x3
+ 6xy - 3y2 = 0 3x2dx + 6ydx + 6xdy - 6ydy = 0 dx(3x2 + 6y) = dy(6y - 6x) dy/dx = (3x² + 6y)/(6y - 6x) evenwijdig aan de x-as: 3x2 + 6y = 0 y = -1/2x2 invullen : x3 - 3x3 - 3/4x4 = 0 2x3 + 3/4x4 = 0 x3(2 + 3/4x) = 0 x = 0 ∨ x = -8/3 dus dat zijn de punten (0, 0) en (-8/3, -32/9) evenwijdig aan de y-as 6y - 6x = 0 y = x invullen: x3 + 6x2 - 3x2 = 0 x3 + 3x2 = 0 x2(x + 3) = 0 x = 0 ∨ x = -3 dus dat zijn de punten (0,0) en (-3, -3) Het punt (0, 0) heeft helling 0/0 dus dat is onbekend.... |
|||
| b. | p3
+ 6py - 3y2 = 0 ABC-formule: y = (-6p ±√(36p² + 12p³))/-6 = p ± 1/6√(36p2 + 12p3) De afstand daartussen is 2/6√(36p2 + 12p3) Dat is minimaal als dat deel onder die wortel minimaal is, dus als de afgeleide ervan nul is: 72p + 36p2 = 0 36p(2 + p) = 0 p = 0 ∨ p = -2 De gezochte waarde is p = -2, en dan is de afstand AB = 2/6√(144 - 96) = 1/3√48 = 4/3√3 |
||||
| c. | x3
+ 6x(qx) - 3(qx)2 = 0 x3 + x2(6q - 3q2) = 0 x2 (x + 6q - 3q2) = 0 x = 0 ∨ x = 3q2 - 6q Dat heeft maar ιιn oplossing als deze twee oplossingen samenvallen. 3q2 - 6q = 0 3q(q - 2) = 0 q = 0 ∨ q = 2 |
||||
| d. |
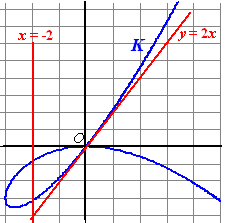 |
||||
| 4. | x
- ylny = 0 dx - lnydy - y 1/y dy = 0 dx = dy(lny + 1) dy/dx = 1/(lny + 1) evenwijdig aan de x-as kan niet, want dy/dx wordt nooit nul. evenwijdig aan de y-as: lny + 1 = 0 lny = -1 y = e-1 =1/e Dan is x - 1/e -1 = 0 dus x = -1/e en het punt is (-1/e, 1/e) |
||||
| 5. | a | x = 0 geeft
y3(a - y) = 0 dus y =
0 of y = a Je kunt a dus aflezen op de y-as bij het snijpunt. De groene en de blauwe hebben a = 2, de rode heeft a = 1 Lees voor het berekenen van b een ander punt af. groen: (1.3, 1.5) invullen: b2 1,69 = 1,53 (2 - 1,5) ⇒ b2 = 1 ⇒ b = 1 blauw: (0.9, 1.5) invullen: b2 0,81 = 1,53 (2 - 1,5) ⇒ b2 = 2 ⇒ b = √2 rood: (0.3, 0.7) invullen: b2 0,09 = 0,73 (1 - 0,7) ⇒ b2 = 1,14 ⇒ b = 1,07 |
|||
| b. |
b2x2 = y3(a -
y) b2x2 = ay3 - y4 2b2xdx = 3ay2 dy - 4y3dy dy/dx = 2b²x /(3ay² - 4y³) verticaal als 3ay2 - 4y3 = 0 y2(3a - 4y) = 0 y = 0 ∨ y = 3/4a Die laatste is gelijk aan 6, dus 3/4a = 6 ⇒ a = 8 (√3, 6) invullen: 3b2 = 216(8 - 6) 3b2 = 432 b2 = 144 b = 12 |
||||
| c. | de verticale raaklijn
zit bij y = 3/4a
(zie vraag b) invullen: b2x2 = (3/4a)3 (a - 3/4a) b2x2 = 27/256 a4 x2 = (27a4)/(256b²) x = ±√((27a4)/(256b²) ) de breedte B is dan tweemaal die wortel, en dat geeft de gevraagde formule. |
||||
| 6. | a. | x2 + (y2
- 1)2 = 1 x2 + y4 - 2y2 + 1 = 1 3xdx + 4y3dy - 4ydy = 0 3xdx = dy(4y - 4y3) dy/dx = 3x/(4y - 4y³) De raaklijn is verticaal als 4y - 4y3 = 0 4y(1 - y2) = 0 y = 0 ∨ y = 1 ∨ y = -1 y = 0 vervalt, want dan is ook x= 0 en is de helling 0/0 y = ±1 geeft x2 = 1 dus x = 1 ∨ x = -1 Het zijn de punten (1,1)(-1,1)(1,-1)(-1,-1) |
|||
| b. | x2 + (p2
- 1)2 = 1 x2 = 1 - (p2 - 1)2 x = ±√(1 - (p2 - 1)2 ) dan is AB = 2√(1 - (p2 - 1)2 ) = √3 4(1 - (p2 - 1)2 ) = 3 4(1 - p2 + 2p - 1) = 3 -4p2 + 8p - 3 = 0 p = (-8 ±√(64 - 48))/-4 = 3 of 1 |
||||
| 7. | a. |
x4 - 4x2 + 4(px)2 = 0 x4 + x2(-4 + 4p2) = 0 x2 (x2 - 4 + 4p2) = 0 x2 = 0 ∨ x2 = 4 - 4p2 x = 0 x = ±√(4 - 4p2) Dat laatste heeft twee verschillende oplossingen (ongelijk 0) als 4 - 4p2 > 0 4p2 < 4 p2 < 1 -1 < p < 1 |
|||
| b. |
x4 - 4x2 + 4y2 = 0 4x3dx - 8xdx + 8ydy = 0 8ydy = dx(8x - 4x3) dy/dx = (8x - 4x³)/8y raaklijn evenwijdig aan de x-as: 8x - 4x3 = 0 4x(2 - x2) = 0 x = 0 ∨ x = √2 ∨ x = -√2 x = 0 vervalt want dan is ook y = 0 en dat geeft helling 0/0 x = √2 geeft 4 - 8 + 4y2 = 0 en daaruit volgt y = 1 ∨ y = -1 Dat zijn de punten (√2, 1) en (√2, -1) raaklijn evenwijdig aan de y-as: 8y = 0 dus y = 0 dat geeft x4 - 4x2 = 0 x2(x2 - 4) = 0 x = 0 ∨ x = 2 ∨ x = -2 x = 0 vervalt want dan is ook y = 0 en dat geeft helling 0/0 Dat zijn de punten (2, 0) en (-2, 0) |
||||
| 8. | a. | De kromme gaat
bijvoorbeeld door (1, 2) y2 = ax4 - x2 geeft dan 4 = a - 1 Dus a = 5 |
|||
| b. | y2
= x4 - x2 2ydy = 4x3dx - 2xdx dy/dx = (4x³ - 2x)/2y = (2x³ - x)/y Als dat -1 is, dan geldt dus y = -2x3 + 2x Invullen in de vergelijking van K1: (-2x3 + 2x)2 = x4 - x2 4x6 - 8x4 + 4x2 = x4 - x2 4x6 - 9x4 + 5x2 = 0 x2(4x4 - 9x2 + 5) = 0 x = 0 ∨ x2 = (9 ±√1)/8 x = 0 ∨ x2 = 1 ∨ x2 = 5/4 x = 0 ∨ x = 1 ∨ x = -1 ∨ x = 1/2√5 ∨ x = -1/2√5 De eerste drie geven allemaal y = 0 en dan bestaat de helling niet. x = ±1/2√5 geeft y2 = 5/16 dus y = ±1/4√5 Controleren of de hellingen inderdaad -1 zijn geeft de punten (-1/2√5, 1/4√5) en (1/2√5, -1/4√5) |
||||
| c. | (0, 0) voldoet wel
aan de vergelijking van K, dus ligt op K. Maar zodra x naar nul gaat, is ax4 - x2 kleiner dan nul (hoe groot a ook is, op een gegeven moment zorgt die x4 er toch voor dat ax4 kleiner wordt dan x2) Dat betekent dat vlak bij nul er geen punt op K ligt, want y2 kan niet negatief zijn. De oorsprong is een los, geοsoleerd punt van K. |
||||
| 9. | a. | y2
= x3 + 3x2 2ydy = 3x2 dx + 6xdx dy/dx = (3x² + 6x)/2y x = 6 geeft y2 = 324 dus y = ±18 in (6, 18) is dy/dx = 4 dus de raaklijn is y = 4x + b 18 = 4 6 + b geeft b = -6 en de raaklijn is y = 4x - 6 in (6, -18) is dy/dx = -4 dus de raaklijn is y = -4x + b -18 = -4 6 + b geeft b = 6 en de raaklijn is y = -4x + 6 4x - 6 = -4x + 6 8x = 12 x = 1,5 en dan is y = 0 S = (1.5, 0) |
|||
| b. | dy/dx
= 0 als 3x2 + 6x = 0 3x(x + 2) = 0 x = 0 ∨ x = -2 x = 0 vervalt want dan is dy/dx = 0/0 x = -2 geeft y2 = 4 Het zijn de punten (-2, 2) en (-2, -2) |
||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||