© h.hofstede (h.hofstede@hogeland.nl)

       
De methode van de onbepaalde coλfficiλnten
       
De algemene gedaante van lineaire differentiaalvergelijkingen was deze:
       

y(n) + an - 1 • y(n - 1)  +  an - 2 •  y(n - 2)  + ... + a2 • y ''  + a1 • y'  + a0  • y =  f(x)
       
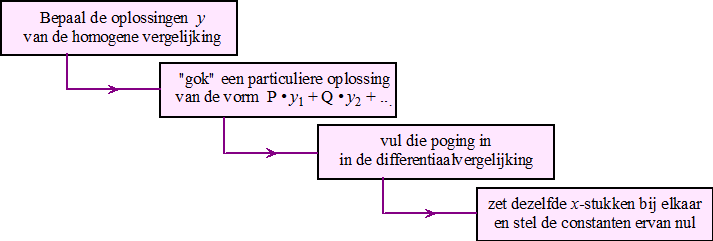
De vorige les hebben we gezien hoe je homogene differentiaalvergelijkingen van hogere orde oplost. We gaan het verhaal nu afmaken door te bestuderen hoe je particuliere oplossingen van zulke differentiaalvergelijkingen kunt vinden. Bij tweede orde vergelijkingen hadden we daarvoor twee  methoden, namelijk de methode van de onbepaalde coλfficiλnten en de methode van Variatie van parameters.
Die beide methodes blijken, met kleine aanpassingen, ook voor hogere orde differentiaalvergelijkingen te gelden.

Eerst zijn de onbepaalde coλfficiλnten aan de beurt.  Lees deze les daarover eerst weer door.

Kort samengevat was dit de methode:
       

       
Bedenk daarbij nog dat termen in onze "gok" niet hetzelfde moeten zijn als termen uit de oplossing van de homogene vergelijking.  Als in het niet-homogene deel toch dezelfde termen staan, dan moet je meestal  je gok met x vermenigvuldigen, kijk maar:

snel voorbeeldje:
Los op   y'' +  y'  - 6y = 4e2x
Je zou graag willen gokken  y = P • e2x 
Maar de karakteristieke vergelijking is  λ2 + λ - 6 = 0 en die heeft oplossingen λ = 2 en λ = -3
De homogene vergelijking heeft oplossingen  e2x en e-3x   dus en daar zit die e2x die je wilde gokken al in.
Probeer daarom  y = Px • e2x
Dat geeft  y' =  Pe2x + 2Pxe2x   en  y'' = 2Pe2x + 2Pe2x + 4Pxe2x  = 4Pe2x + 4Pxe2x
Invullen:   4Pe2x + 4Pxe2x +  Pe2x + 2Pxe2x - 6Pxe2x = 4e2x 
e2x • (4P + P - 4)  + xe2x • (4P + 2P - 6P) = 0
Dat geeft  P =  0,8  en een particuliere oplossing  y = 0,8xe2x

Nou, bij hogere orde differentiaalvergelijkingen gaat het precies zo. Het enige verschil is, dat er nu in de oplossingen van de homogene vergelijking al termen met  x2 zouden kunnen staan, dus dan zou je in je gok termen met nog hogere machten van x ervoor nodig kunnen hebben.

Echt Voorbeeld dan maar:   Geef een particuliere oplossing van:   y''' - 6y'' + 12y'  - 8y =  2 + e3x  - 2e2x
Karakteristieke vergelijking:  λ3 - 6λ2 + 12λ - 8 = 0   en dat is gelijk aan   (λ - 2)3  = 0
Dat geeft drie keer de oplossing  λ = 2
De oplossing van de homogene vergelijking is   y = Ae2x + Bxe2x + Cx2e2x

We willen graag gokken  iets met  e3x  en e2x  maar omdat die e2x al in de oplossing van de homogene vergelijking  staat (zelfs al drie keer)  zal dat nu de gok  x3e2x  moeten worden.
De gok is daarom:  y =  P + Qe3x + Rx3e2x
Dat geeft 
y' =  3Qe3x + 2Rx3e2x + 3Rx2e2x 
y'' = 9Qe3x + 4Rx3e2x + 12Rx2e2x + 6Rxe2x
y''' = 27Qe3x + 8Rx3e2x + 36Rx2e2x + 36Rxe2x + 6Re2x 

Invullen:
27Qe3x + 8Rx3e2x + 36Rx2e2x + 36Rxe2x + 6Re2x  - 6(9Qe3x + 4Rx3e2x + 12Rx2e2x + 6Rxe2x ) + 12(3Qe3x + 2Rx3e2x + 3Rx2e2x) - 8( P + Qe3x + Rx3e2x ) = 2 + e3x  - 2e2x

Rangschikken:
e3x • (27Q - 54Q + 36Q - 8Q - 1) + e2x • (6R - 2)  + xe2x • (36R - 36R) + x2e2x • (36R - 72R + 36R) + x3e2x • (8R - 24R + 24R - 8R)  + (-8P - 2) = 0
Dat geeft   Q = 1 en  R = 1/3 en  P = 1/4
Een particuliere oplossing is  y =  1/4 + e3x + 1/3x3e2x
       
Wat zou ik gokken?

Welke "gok" je neemt voor een particuliere oplossing hangt nogal af van de vorm van f(x). Dat zagen we al in beide voorbeelden. We zullen er nu een beetje gestructureerder naar kijken.

Ik zou de volgende volgende particuliere oplossingen gokken:
(Met Vn(x)  en  Pn(x) en  Qn(x) bedoel ik ιιn of andere veelterm in x van graad n, en p is steeds de multipliciteit van de wortel van de karakteristieke vergelijking (dat is hoe vaak dezelfde wortel voorkomt)).
       
  Hoe ziet  f(x) eruit? Wat zou ik gokken?
1
n
2n
 
3n
 
4
ixn
Vn(x)
 
Vn(x) • eαx 
 
cos(βx)eαx   of   sin(βx)eαx
 
cos(βx) • Vn(x)   of  sin(βx) • Vn(x)
 
xp •  Pn(x)
    als 0  een oplossing van de karakteristieke vgl. is met mult.  p
xp • Pn(x) • eαx 
    als α een oplossing van de karakteristieke vgl. is met  mult.  p
xp • eαx • (acosβx + bsinβx)
    als α + βi een oplossing van de karakteristieke vgl.  is met  mult.  p
xp • Pn(x) • cos(βx) + xp • Qn(x) • sin(βx)
    als βi een oplossing van de karakteristieke vgl. is met  mult.  p
       
Vijf  Gokvoorbeelden.
     

•

 Los op:   y'' + y ' = sinx
    Karakteristieke vergelijking  λ2 + λ = 0  heeft  λ  = 0   ∨   λ  = -1
Dit is geval 3 uit de tabel met α = 0 en β = 1
0 + i  is geen oplossing van de karakteristieke vergelijking (p = 0)
Ik zou daarom proberen   y =  acosx + bsinx
   
• Los op:   y'' - 2y' + 2y = 1 + x + e-x + sin3x • e2x 
    Karakteristieke vergelijking  λ2 - 2λ + 2 = 0  heeft  λ = 1 ± i
• 1 + x  (geval 1) met 0 geen wortel geeft poging y = a + bx
•  e-x  (geval 2) met -1 geen wortel geeft poging  y = ae-x
•  sin3x • e2x  (geval 3) met 2 + 3i geen wortel geeft poging
    y = ae2xsin3x + be2xcos3x
Los deze drie gevallen apart op, en tel ze bij elkaar op voor de particuliere oplossing.
       
• Los op:  y" + 3y'  = 2x3 - 1  + xe-3x
    Karakteristieke vergelijking  λ2 + 3λ = 0  heeft  λ = 0  ∨ λ  = -3 
•  2x3 - 1  (geval 1)  met 0 wel een wortel (met p = 1)   geeft poging  y = x1 • (ax3 + bx2 + cx + d)
•  xe-3x  (geval 2) met -3 wel een wortel  (met p = 1) geeft poging   y = x1 • (ax + b) • e-3x  
Los deze twee gevallen apart op en tel ze bij elkaar op voor de particuliere oplossing
       
• Los op:  y'' + 2y' + 2y = 3cos4x + cosx • ex - 2sinxe-x
    Karakteristieke vergelijking  λ2 + 2λ + 2 = 0  heeft  λ = -1 ± i
•  3cos4x (geval 3) met 0 + 4i geen wortel geeft  poging  y = acos4x + bsin4x
•  cosx • ex  (geval 3) met  1 + i  geen wortel geeft poging  y = (acosx + bsinx) • ex
•  -2sinx • e-x  (geval 3) met -1 + i  wel een wortel (p = 1) geeft poging   y =  x • (acosx + bsinx) • e-x
Los deze drie gevallen apart op en tel ze bij elkaar op voor de particuliere oplossing.
       
• Los op:  y'' + y = -3x2sin2x + xcosx  
    Karakteristieke vergelijking  λ2 + 1 = 0  heeft  λ = ± i
•  3x2sin2x  (geval 4) met  2i  geen wortel  geeft poging  y = (ax2 +bx + c) • sin2x + (dx2 + ex + f) • cos2x
•  xcosx  (geval 4) met i  wel een wortel  (p = 1) geeft  poging  y = x(ax + b)sinx + x(cx + d)cosx
Los deze twee gevallen apart op en tel ze bij elkaar op voor de particuliere oplossing.
       
       

  OPGAVEN
       
1. Geef algemene oplossingen van de differentiaalvergelijkingen uit de vijf gokvoorbeelden hierboven.
       
2. Een homogene ketting met lengte 15 m hangt over een balk:  4 meter aan de ene zijde, 11 meter aan de andere zijde. De wrijvingsweerstand van de balk is gelijk aan het gewicht van een halve meter ketting.

Voor de beweging van de ketting geldt:    15x'' = 6,5g  + 2xg  met  x(0) = x'(0) = 0

(met daarin  x =  het stuk afgegleden ketting in m en   g = zwaartekrachtsversnelling)
       
  a. Toon aan dat deze differentiaalvergelijking geldt.
       
  b. Bereken de tijd die de ketting nodig heeft om van de balk te glijden.
     

1,26 sec.
     

© h.hofstede (h.hofstede@hogeland.nl)