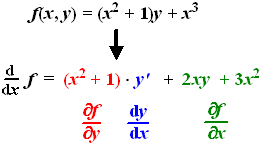|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Stel dat jij leraar wiskunde
bent, en je hebt zin om jouw klas eens een extra moeilijk
differentiaalvergelijking te geven. Gewoon om te pesten (of om ze
"scherp te houden" dat klinkt beter). Dan zou ik het volgende doen: Kies één of andere willekeurige functie van x en y, bijvoorbeeld f(x, y) = (x2 + 1)y + x3 Bereken hiervan nu df/dx Bedenk daarbij dat die y's allemaal ook functies van x zijn, dus bij het differentiëren moet je de productregel en de kettingregel gebruiken. Dat geeft in dit geval df/dx = 2x • y + (x2 + 1) • y' + 3x2 = (x2 + 1) • y' + 2xy + 3x2 Als je nu stelt df/dx = 0 dan staat er: (x2 + 1) • y' + 2xy + 3x2 = 0 en dat is een lekkere lastige differentiaalvergelijking. Maar ik weet de oplossing ervan al! Immers df/dx = 0 geeft f = c dus de oplossing van mijn "moeilijke" differentiaalvergelijking is (x2 + 1)y + x3 = c c hangt daarbij natuurlijk van de beginvoorwaarde af. Gelukt! Ik geef mijn leerlingen de differentiaalvergelijking (x2 + 1) • y' + 2xy + 3x2 = 0 zonder natuurlijk iets te verraden over die f(x, y) die eraan te grondslag lag. Laat ze daar maar eens uit zien te komen...... Om dat te doen moeten ze één of andere manier vinden om alles wat ik hierboven heb gedaan in de omgekeerde richting uit te voeren.... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Kan het in de omgekeerde richting? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Een differentiaalvergelijking die
je kunt schrijven als f(x, y) = 0 met
één of andere nog mysterieuze functie f heet een
Exacte Differentiaalvergelijking
(het wordt ook wel een Totale Differentiaalvergelijking
genoemd). We moeten nu twee vragen beantwoorden: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
vraag 1: Hoe weet je of een
gegeven differentiaalvergelijking exact is? Dat kun je het best zien door eens goed te kijken naar die afgeleide df/dx. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Daarin zie je dat geldt:
d/dx f(x, y) =
∂f/∂y
• y' + ∂f/∂x
Die vreemde kromme ∂'s staan voor de partiële afgeleiden. Dus als een differentiaalvergelijking er uitziet als P • y' + Q = 0 dan weten we nu intussen dat, als het een exacte differentiaalvergelijking is, er een f bestaat zodat P = ∂f/∂y en Q = ∂f/∂x Maar dat betekent dat, als je P naar x differentieert, je hetzelfde moet krijgen als wanneer je Q naar y differentieert. In beide gevallen differentieer je de functie f naar x én naar y. Dat is een mooie test of een differentiaalvergelijking exact is: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Deze voorwaarde heet ook wel de "voorwaarde van Euler". Denk erom dat de differentiaalvergelijking wel op nul herleid moet zijn. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Toegepast op bovenstaand
voorbeeld: ∂P/∂x = ∂/∂x(x2 + 1) = 2x en ∂Q/∂y = ∂/∂y(2xy + 3x2) = 2x dus dat klopt inderdaad! |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| vraag 2: Hoe vind je die mysterieuze functie f ? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Het antwoord op deze vraag ligt
in het feit dat je die P en Q kent: P = ∂f/∂y
en Q = ∂f/∂x Die kun je primitiveren! Kies één van beiden (neem degene die het makkelijkst te primitiveren lijkt). In bovenstaand voorbeeld hadden we P = x2 + 1 en Q = 2xy + 3x2 Laten we bijvoorbeeld P kiezen om te primitiveren. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Let goed op! De integraal is met de variabele y, dus kun je x2 + 1 als een constante zien. Daar zit immers geen y in. Verder is de primitieve altijd op een constante na bepaald, maar die constante kan hier een functie van x zijn (h(x)). Immers om die P te maken zijn alle stukken met alleen x-en als constanten beschouwd en die zijn bij het differentiëren weggevallen. De voorlopige stand is dus f(x, y) = (x2 + 1)y + h(x) Nu gaan we met deze voorlopige f de Q bepalen: Q = ∂f/∂x = 2xy + h'(x) en dat moet gelijk zijn aan 2xy + 3x2 Dat geeft h'(x) = 3x2 en primitiveren geeft dan h(x) = x3 + c. Samen geeft dat f(x, y) = (x2 + 1)y + x3 + c De differentiaalvergelijking (x2 + 1) • y' + 2xy + 3x2 = 0 heeft dus als oplossing (x2 + 1)y + x3 = c (waarbij die c nog uit de beginvoorwaarde volgt). tot slot een paar kleinigheidjes. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| • | Merk nog op dat je in dit geval de oplossing altijd als een impliciete vergelijking krijgt (dat is een vergelijking met y en x door elkaar). Soms is het mogelijk daarvan te maken y = .... maar dat hoeft niet altijd te lukken. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| • | Denk erom dat je de
vergelijking eerst op nul herleidt voordat je de voorwaarden ∂P/∂x
= ∂Q/∂y
controleert Zo is de vergelijking (y - x)dx = (x + y)dy NIET exact! |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| • | Als je een exacte
differentiaalvergelijking met x of y vermenigvuldigt is
het resultaat meestal niet meer exact. Je mag een exacte
differentiaalvergelijking dus niet "om te vereenvoudigen" met x
of y vermenigvuldigen! Omgekeerd kun je sommige differentiaalvergelijkingen die niet exact zijn door een geschikte vermenigvuldiging veranderen in exacte differentiaalvergelijkingen. Dat zagen we al in de les over de integrerende factor. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||