Functies van twee variabelen.

© h.hofstede (h.hofstede@hogeland.nl)
       
Het Probleem:

Stel dat ik een zinken plaat heb van 3 meter lang en 25 cm breed, en daar wil ik een dakgoot van 3 meter lang van maken.
Dat kan ik doen door twee zijkanten over een bepaalde hoek a omhoog te buigen,  zoals je hieronder ziet.
       

       
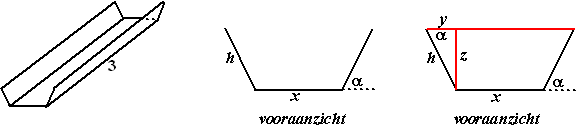
Ik maak de dakgoot symmetrisch want dat vind ik mooi. Dat betekent dat de beide zijkanten even lang zijn, en onder dezelfde hoek zijn omgebogen. De grote vraag is nu:  Hoe kunnen we ervoor zorgen dat de dakgoot zoveel mogelijk water kan verwerken?

In Den Beginne:

De goot zal zoveel mogelijk water kunnen verwerken als de oppervlakte van het vooraanzicht in de middelste figuur hierboven maximaal is.
Die oppervlakte is gelijk aan  O = xz + yz (zie de rechterfiguur hierboven).
Maar omdat z = hsinα  en  y = hcosα  wordt dat  O =  hxsinα +  h2sinαcosα

Kijk!  Dat schiet al lekker op:   nu staan er nog maar drie onbekenden in de formule voor O.
Kunnen we nóg een letter wegwerken?  Jazeker!  We hebben nog niet gebruikt dat de plaat 25 cm breed was.
Dat geeft extra voorwaarde  x + 2h = 25  ofwel  x = 25 - 2h
Invullen in de formule voor O geeft  O = h(25 - 2h)sinα + h2 sinαcosα =  25h - 2h2sinα + h2sinαcosα
 
 

O = 25hsinα - 2h2sinα + h2sinαcosα
 

En nou wil het niet verder!
Er zijn  geen extra voorwaarden meer. Dus er valt geen letter meer weg te werken....Die h en die α raken we nooit kwijt.

Helaas helaas. We zouden nu graag  "afgeleide = nul"   gaan doen, maar een formule met twee letters kunnen we niet differentiëren.
       
Een Goddelijke Ingeving.
       
Ach nou ja, als je gelovig bent kun je natuurlijk altijd gaan bidden tot je God (welke dat ook moge zijn). Misschien wil hij (zij?) jou de oplossing wel gewoon geven....

Oké, stel dat dat lukt. Je hebt heel hard gebeden, en uiteindelijk heeft God jou de waarde van h waarvoor de oppervlakte maximaal is verraden. Laten we die waarde door de hoofdletter H voorstellen. (hij komt immers van God, dus een hoofdletter is wel op zijn plaats lijkt me).

Dan weet je dus dat  O = 25Hsinα - 2H2sinα + H2sinαcosα
Daarin is die H nu een vast getal (aan een mededeling van God valt natuurlijk niet te twijfelen).
 

Maar dan kun jij nu zelf de bijbehorende beste hoek α uitrekenen.
Immers als O maximaal moet zijn dan moet je (met die gegeven vaste H) nu α zó kiezen dat de afgeleide van O nul is.

Dat geeft (met de productregel voor sinαcosα):    O'  = 25Hcosα - 2H2 cosα + H2cos2α - H2sin2α = 0

Fatsoeneren:
⇒ 25Hcosα - 2H2 cosα + H2cos2α - H2(1 - cos2α) = 0
⇒ 25Hcosα - 2H2cosα + 2H2cos2α - H2 = 0  
⇒  H • (25cosα - 2Hcosα + 2Hcos2α - H) = 0
omdat H niet nul is geeft dat uiteindelijk:   25cosα - 2Hcosα + 2Hcos2α - H = 0

Dus als je H weet, dan weet je ook α.....
       
De Tip van Allah.

Maar natuurlijk als je een andere god hebt,  bijvoorbeeld Allah, dan vertelt Allah  je misschien wel de waarde van a waarvoor O maximaal is, in plaats van de waarde van h.   Alle Goden zijn nou eenmaal niet gelijk.

Als we die beste waarde voor α dan A noemen, dan geeft dat   O  =  25hsinA - 2h2sinA + h2sinAcosA.
En dan ga je natuurlijk de h  berekenen waarvoor O' = 0:    25sinA - 4hsinA + 2hsinAcosA = 0   

De Goden Werken Eindelijk Eens Samen...

Als we beide rode vergelijkingen samenvoegen (en alles weer even gewoon h en a noemen, alsof het weer onbekend is), dan krijgen we het volgende stelsel:
 

25cosα - 2hcosα + 2hcos2α - h = 0
 25sinα - 4hsinα + 2hsinαcosα = 0 
 

Nou JA!!!! Dat is een stelsel met twee vergelijkingen en dat is in principe op te lossen.  Zonder Goden!!!

Deel de onderste vergelijking door sinα   (dat mag want 0 < α < 90º):
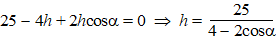Invullen in de bovenste vergelijking:

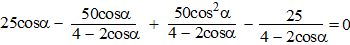vermenigvuldig alles met (4 - 2cosα):

⇒  25cosα(4 - 2cosα) - 50cosα + 50cos2α - 25 = 0 
⇒  100cosα - 50cos2α - 50cosα + 50cos2α - 25 = 0
⇒  50 cosα = 25 
⇒  cosα = 1/2
⇒  α = 60º.

Dat geeft dan  h = 25/3  en daarna   O = 625/12√3 ≈ 90,2 cm2
       
Partieel Differentiëren.

De differentieertechniek die we hier gebruikten heet partieel differentiëren.
Het komt erop neer dat je bij een functie van meerdere variabelen steeds doet alsof je ze allemaal op één na weet, en alsof die ene dan degene is waarmee je de afgeleide moet bepalen.

notatie.
Omdat je bij een functie f  met meerdere variabelen moet aangeven welke variabele degene was waarnaar je differentieert, kun je voor de afgeleide niet meer gewoon opschrijven f ' .
Net zoals we "vroeger" ook wel schreven y' = dy/dx geven we dat nu aan met scheve d's.
∂y/∂x betekent:  de afgeleide nemen met als variabele de x (dus de rest van de variabelen als constanten beschouwen).

In het voorbeeld hierboven zouden we moeten noteren:
∂O/∂α  =  25cosα - 2hcosα + 2hcos2α - h,   en dit geeft aan hoe de oppervlakte verandert als a verandert bij vaste h
∂O/∂h  =  25sinα - 4hsinα + 2hsinαcosα,   en dit geeft aan hoe de oppervlakte verandert als h verandert bij vaste α.

Voorbeeld.
Neem de functie  f(x, y, z) = 3x4z  + z√y - xy3 + 2x

Voor ∂f /∂x moet je y en z als constanten opvatten, dus  ∂f /∂x = 12x3z - y3 + 2
Voor ∂f /∂y moet je x en z als constanten opvatten, dus  ∂f /∂y = z/2√y - 3xy2
Voor ∂f /∂z  moet je x en y als constanten opvatten, dus ∂f /∂z = 3x4 + √y
       
           
1. Bereken de volgende afgeleiden:
           
  a1. ∂y/∂a  met  y = 4a2b3 + 2a a2. ∂y/∂b  met  y = 4a2b3 + 2a
           
  b1. ∂P/∂x  met  P = y√x + 3xy b2. ∂P/∂y  met  P = y√x + 3xy
           
  c1. ∂x/∂q  met  x = 2y/q - q4y2 + 3y c2. ∂x/∂y  met  x = 2y/q - q4y2 + 3y
           
2. Bereken de volgende afgeleiden:
           
  a1. a2.
           
  b1. b2.
           
  c1. c2.
           
3. De doos (zonder deksel) hiernaast heeft afmetingen l bij b bij h.
Je moet zo'n doos ontwerpen, maar je moet daar 8 m2 karton voor gebruiken.

Voor de inhoud geldt:

 

       
  a. Toon dat aan.  
           
  b. Bereken het maximaal te maken volume van zo'n doos.
         

2,18 m3
           
       
Zadelpunten.
       
Neem een functie  van twee variabelen:  z(x, y)
Dan zal de grafiek daarvan een ruimtelijk vlak zijn. De x-as en de y-as geven de waarden van de variabelen x en y en de z-as geeft de uitkomst van de formule.

We zagen al eerder dat ∂z/∂x aangeeft hoe z varieert als x varieert met constante y. Dat is dus de helling van dat z-vlak in de x-richting, of ook wel de richtingscoëfficiënt van de raaklijn aan dat vlak in de x-richting..
En op dezelfde manier geeft ∂z/∂y de helling in de y-richting, en de richtingscoëfficiënt van de raaklijn aan het z-vlak in de y-richting.
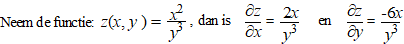Als je bijvoorbeeld deze hellingen in het punt  (2, 1, 4) bekijkt dan geeft dat  ∂z/∂x = 4  en  ∂z/∂y = -12
Het kan dus heel goed dat de helling in de ene richting positief is, en in de andere richting negatief.

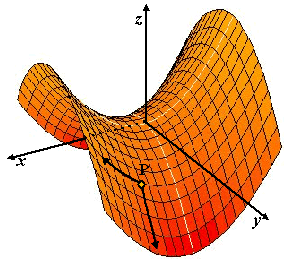
Neem bijvoorbeeld het z-vlak hiernaast.
Daar is in punt P de helling in de x-richting positief (het vlak gaat naar die kant omhoog) maar de helling is de y-richting is negatief (het vlak gaat naar die kant omlaag).

Maar dat betekent dat het feit dat ∂z/∂x en ∂z/∂y beiden gelijk aan nul zijn nog niet wil zeggen dat we te maken hebben met een maximum of minimum van z.
Kijk maar in het vlak hiernaast in de oorsprong. Daar zijn de beide partiële afgeleiden nul, maar er is geen maximum/minimum.
Dat komt natuurlijk omdat z in de x-richting een minimum heeft en in de y-richting een maximum.
Zo'n punt heet een zadelpunt (het vlak lijkt ook wel wat op een zadel, vind je niet?)

       
In het voorbeeld van de dakgoot hierboven hadden we dus nog moeten controleren of O(α) en O(h) wel beiden een maximum bereikten (dat was trouwens wél zo)..... gelukkig maar...
       
           
4. Onderzoek of de volgende functies maxima, minima of zadelpunten hebben.
           
  a. f(x, y) = x2 - y2
           
  b. f(x, y) = x3 + y3 - 3xy      
           
  c. f(x, y) = x/y + 8/x - y      
           
5. Hiernaast zie je een aantal hoogtelijnen van een functie z(x, y)

Leg uit of  ∂z/∂x en  ∂z/∂y positief of negatief zijn in punt P.
       
   
           
6. Voor de vervangingsweerstand R van twee parallel geschakelde weerstanden R1 en R2 geldt:
 
  Stel een vergelijking op voor de snelheid waarmee R varieert als R1 varieert.
           
7. De cosinusregel luidt:  a2 = b2 + c2 - 2bc • cosα
Stel een vergelijking op voor de snelheid waarmee zijde a varieert als zijde b varieert.
           
           
       

© h.hofstede (h.hofstede@hogeland.nl)