|
|
 |
|
De Continuïteitscorrectie. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|
| Op een golfbaan worden vaak
verkeerd geslagen golfballen door de spelers niet teruggevonden. Na
sluitingstijd van de baan gaan kinderen uit de buurt nog vaak golfballen
zoeken in de struiken en bosjes om die dan later voor een paar
dubbeltjes per stuk te verkopen aan golfers. Voor het aantal gevonden
golfballen per dag geldt de volgende tabel: |
|
|
| aantal ballen |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
| frequentie |
1 |
2 |
3 |
5 |
8 |
11 |
14 |
18 |
21 |
24 |
25 |
24 |
|
|
|
| aantal ballen |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
| frequentie |
22 |
19 |
16 |
12 |
9 |
6 |
4 |
2 |
1 |
1 |
0 |
0 |
|
|
|
| Dit aantal golfballen blijkt een
bijna perfecte normale verdeling te volgen. Een grafiek op
normaal-waarschijnlijkheidspapier geeft een kaarsrechte lijn! Als ik het
aantal ballen in L1 van mijn GR zet, en de frequentie in L2, en dan via
STAT-CALC-1VarStats(L1, L2) het gemiddelde en de standaarddeviatie
bereken vind ik
μ = 28,2 en
σ = 3,94. |
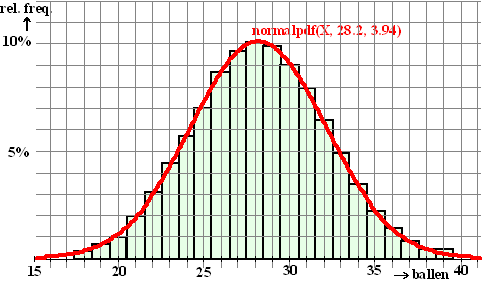
Hiernaast zie je hoe griezelig
goed dat past bij de tabel. In de figuur hiernaast staat het histogram van de tabel in één
figuur met de grafiek van Y1 = normalpdf(X, 28.2, 3.94).
Laten we het met een berekening gaan testen. We bekijken de kans dat er
op een dag meer dan 32 ballen worden gevonden.
De normale verdeling levert op:
normalcdf(32, 1000, 28.2, 3.94) = 0,167
Ofwel 16,7%. |
 |
In de tabel zien we dat er 35 van de 248 dagen meer dan 30 ballen waren
gevonden. Dat zou een percentage van 70/248 • 100%
= 14,1% moeten opleveren!
Dat scheelt nogal veel met elkaar!!!!! |
|
|
|
Wat is hier aan de hand? |
|
|
Alhoewel de twee figuren heel goed
met elkaar overeenkomen vinden we met onze berekeningen toch een groot
verschil. Hoe kan dat? Dat kan nooit komen door die kleine stukjes
histogram die boven de klokvorm uitsteken of er juist onder blijven. Die
zijn veel te klein om een verschil van meer dan 2,5% te geven. Bovendien
heffen die kleine afwijkinkjes boven en onder de klokvorm elkaar ook nog
eens grotendeels op.
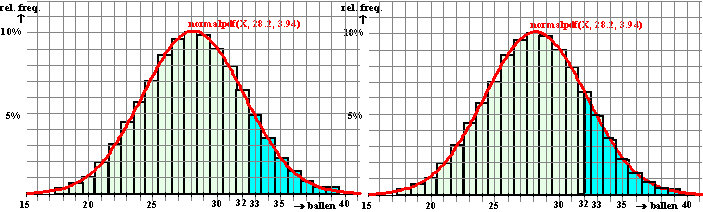
Waar dat verschil dan wél vandaan komt zie je als je de oppervlaktes die
je berekent met het histogram en met de klokvorm wat nauwkeuriger met
elkaar vergelijkt: |
|
|
|
 |
|
|
Kijk goed naar het verschil tussen
de twee blauwe oppervlaktes in de figuren hierboven. Zie je het grote
verschil?
Het zit hem erin dat de meetwaarden op de x-as in het histogram
bij de middens van de staven staan. Dus in de linkerfiguur loopt de
blauwe oppervlakte vanaf staaf 33 maar rechts toe. Maar in de
rechterfiguur letten we niet op staven en nemen we gewoon de oppervlakte
vanaf x = 32 naar rechts toe. Dat scheelt een halve staaf, kijk
maar: |
|
|
|
 |
|
|
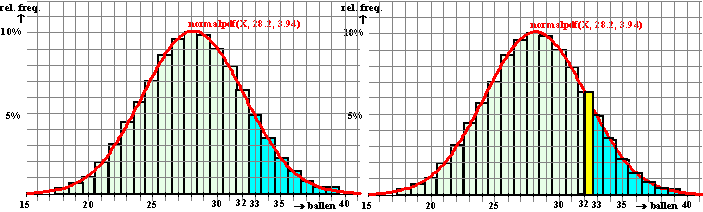
Dat komt dus doordat we een
discrete verdeling (het aantal golfballen moet een geheel getal zijn)
hier benaderen met een continue verdeling (de normale verdeling).
Om een betere overeenkomst te krijgen moeten we een correctie
uitvoeren: ook in de rechterfiguur moeten we die gele staaf niet
meetellen. Dat kan als we als linkergrens niet 32 nemen, maar 32,5.
Dat geeft oppervlakte normalcdf(32.5, 1000, 28.2, 3.94) = 13,8% en
dat lijkt veel beter op de 14,1% van het histogram. Dat scheelt nog niet
eens één golfbal (want die is 0,4%).
Deze correctie (van die halve staaf verschil) komt elke keer voor als je
een discrete verdeling probeert te benaderen door de normale verdeling.
Het heet de continuïteitscorrectie
Let dus goed op: |
| |
|
|
Elke keer als je iets met de normale
verdeling berekent,
maar je wéét dat de verdeling eigenlijk discreet is,
dan moet je de continuïteitscorrectie toepassen. |
|
| |
|
| Het scheelt elke keer een
halve staaf. Je moet dus voor de grenzen van de normale verdeling 0,5
meer of minder nemen. Maak maar gewoon zo'n tekening als hierboven, dan
zie je het vanzelf. |
| |
|
|
OPGAVEN |
| |
|
| 1. |
De politie van Groningen houdt regelmatig
drankcontroles bij automobilisten. Het blijkt dat het aantal
bekeuringen dat men op een avond uitdeelt bij benadering normaal
verdeeld is met een gemiddelde van 46 en een
standaarddeviatie van 8.
Bereken zo nauwkeurig mogelijk de kans dat er op een avond
minstens 56 bekeuringen worden uitgedeeld. |
| |
|
|
|
|
| |
|
|
|
|
| 2. |
Geraldine bezorgt folders als bijbaantje. Ze
krijgt van het distributiebedrijf de folders kant en klaar in
pakketten , verpakt in plastic. Het aantal folders in een
pakket varieert van week tot week. Dat aantal is bij benadering
normaal verdeeld met een gemiddelde van 15 en een
standaarddeviatie van 5.
Hoe groot is de kans dat Geraldine in een bepaalde week pakketen
van minder dan 12 folders moet bezorgen? |
| |
|
|
|
|
| |
|
|
|
|
| 3. |
Joke en Karien spelen elke Zaterdagmiddag in de
kroeg een spelletje biljart. Ze spelen dan steeds 50 beurten, en
tellen het aantal punten dat ze scoren. Een beurt gaat net
zolang door totdat je een keer géén punt scoort. Dus in theorie
kun je in één beurt wel oneindig veel punten scoren.
Het aantal punten dat Joke scoort in 50 beurten is normaal
verdeeld met een gemiddelde van 78 en een standaarddeviatie van
12. Voor Karien is het gemiddelde 75 en de standaarddeviatie 8. |
| |
|
|
|
|
| |
a. |
Hoe groot is de kans dat Joke op een
zaterdagmiddag meer dan 85 punten scoort? |
| |
|
|
| |
b. |
Hoe groot is de kans dat het aantal
punten dat Karien op zaterdagmiddag scoort meer is dan 65 maar
minder dan 80? |
| |
|
|
|
 |
c. |
Hoe groot is de kans dat Karien van
Joke wint? |
| |
|
|
|
|
| |
|
|
|
|
| 4. |
examenvraagstuk VWO Wiskunde A,
1993. In deze opgave gaan we uit van een jaar van
365 dagen. In zo'n jaar telt januari 31, februari 28, maart 31, en april
30 dagen. In deze opgave worden de dagen van het jaar genummerd vanaf 1
januari. 1 februari heeft dan nummer 32.
Voor de bemesting van een
grasland gebruikt men stikstofkunstmest. Uit onderzoek is gebleken dat
de eerste bemesting in het voorjaar het hoogste rendement geeft als men
direct na het bereiken van een temperatuursom (T-som) van 200ºC strooit.
De T-som is de som van de gemiddelde etmaaltemperaturen vanaf 1 januari.
De gemiddelde etmaaltemperatuur per dag wordt telkens de volgende
ochtend berekend en bij de vorige T-som opgeteld. Zodra de T-som meer
dan 200 is, worden de boeren hiervan via de radio op de hoogte gebracht.
De dag waarop dit gebeurt noemen we de melddag.
Uit gegevens over lange tijd blijkt dat het nummer van de melddag bij
benadering normaal verdeeld is met een gemiddelde van 105 en een
standaarddeviatie van 10. |
| |
|
|
|
|
| |
a. |
Bereken de kans dat de melddag
een dag in april is. |
| |
|
|
|
|
| |
De mest moet beslist droog
bewaard worden. Boeren en tussenhandelaren nemen deze daarom niet in
voorraad. Zodra de melddag is aangebroken, wordt de mest bij
kunstmestfabriek KF besteld. KF moet daar rekening mee houden. Bij het
opstellen van een voorlopig jaarschema in december wenst KF dat het
risico van een onvoldoende voorraad stikstofkunstmest op de melddag
kleiner is dan 1%. |
| |
|
|
|
|
| |
b. |
Bereken de uiterste datum die KF
in het voorlopig jaarschema kan opnemen voor het op peil zijn van de
voorraad kunstmest. |
| |
|
|
|
|
| 5. |
examenvraagstuk HAVO Wiskunde B,
2005 (gewijzigd). Demografen houden zich onder andere bezig met
de samenstelling, opbouw en groei van de bevolking. De groei van de
bevolking is onder andere afhankelijk van het aantal geboorten. Neem aan
dat het aantal geboorten per dag in Nederland bij benadering normaal
verdeeld is met een gemiddelde van 550 en een standaardafwijking van 35. |
| |
|
|
|
|
| |
a. |
Bereken op hoeveel dagen van
één jaar er in Nederland naar verwachting 500 of meer geboorten zullen
zijn. |
| |
|
|
|
|
| |
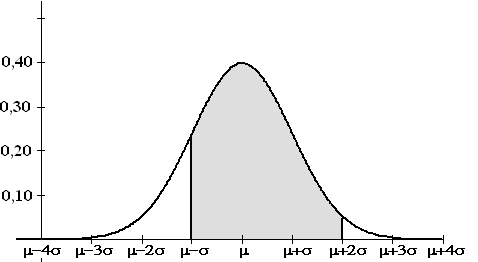
Hieronder is de grafiek van een
normale verdeling getekend met gemiddelde
μ en
standaardafwijking
σ. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
b. |
Bij een continue normale verdeling
is de kans dat een meting tussen
μ - σ
en
μ + 2σ
ligt ongeveer 82%.
Leg dat uit. |
| |
|
|
|
|
| |
c. |
Bereken de kans dat op een
willekeurige dag het aantal geboorten tussen
μ - σ
en
μ + 2σ
ligt. |
| |
|
|
|
|
| |
|
|
|
|
|
|
De binomiale verdeling. |
| |
|
| Dit is het bekendste voorbeeld van
een discrete verdeling, immers hier gaat het steeds om de kans op een
aantal successen en dat aantal moet uiteraard een geheel getal zijn.
Weet je de eigenschappen en notatie nog? |
| |
|
• met terugleggen: kans elke keer
gelijk
• elke keer twee mogelijkheden.
• volgorde is niet van belang.
n = aantal experimenten.
p = kans op succes per experiment.
k = gevraagde aantal successen. |
|
| |
|
| Als het aantal experimenten groter
wordt, dan gaat de binomiale verdeling steeds meer lijken op de normale
verdeling (dat is een gevolg van de centrale limietstelling), dus
kun je hem daarmee benaderen. Daarvoor moet je wél het gemiddelde en de
standaarddeviatie weten en verder moet je, omdat je te maken hebt met
een discrete verdeling, niet vergeten de continuïteitscorrectie toe te
passen. |
| |
|
|
Gemiddelde
en standaarddeviatie van de binomiale verdeling. |
| |
|
Het gemiddelde, daar zul je denk
ik niet al teveel moeite mee hebben. Als bijvoorbeeld de kans op succes
gelijk is aan 1/5 en je verricht 400 experimenten,
hoeveel successen verwacht je dan? Nou, dat lijkt mij gelijk aan 1/5
deel van 400 dus 80 successen. In 1/5 deel
van de gevallen zul je immers succes hebben? En er zijn 400 "gevallen",
nietwaar?
Met p en n in plaats van 1/5 en 400
geeft dat
μ = n • p
De standaarddeviatie s is wat lastiger te
bepalen. Als je graag wilt weten hoe dat gaat, lees dan het bewijs
hieronder.
In ieder geval gelden de volgende twee formules: |
| |
|
|
|
 |
Voorbeeld.
Gooi 40 keer met een dobbelsteen. Benader met de normale verdeling de
kans dat je meer dan 8 zessen gooit en vergelijk deze kans met de exacte
(binomiale) kans.
n = 40, p = 1/6 (succes = zes
gooien).
μ = 40 • 1/6 = 62/3
en
σ = √(40 •
1/6 • 5/6) = 2,357.
continuïteitscorrectie: meer dan 8 is vanaf 8,5. Dus
normalcdf(8.5, 40, 62/3,
2,357) = 0,2183.
Binomiaal: P(X >8) = 1 - P(X ≤
8) = 1 - binomcdf(40, 1/6, 8) = 0,2127.
Dat klopt dus aardig! |
| |
|
| 6. |
We gooien 100 muntstukken en tellen het aantal
keer “kop”. Dat aantal blijkt bij benadering normaal verdeeld
met een gemiddelde van 50. |
| |
|
|
|
|
| |
a. |
Leg uit waarom de standaarddeviatie
gelijk zal zijn aan 5. |
| |
|
|
| |
b. |
Bereken met deze normale benadering
de kans dat bij zo’n experiment het aantal keer kop kleiner is
dan 40, en kijk hoeveel deze benadering afwijkt van het
exacte antwoord. |
| |
|
|
|
|
| |
|
| 7. |
Op een pakje thee staat dat er 100
gram inzit. Natuurlijk zullen niet alle pakjes thee 100 gram
wegen. Het gewicht van de pakjes blijkt normaal verdeeld met een
gemiddelde van 102 gram en een standaardafwijking van 2,2 gram.
Het blijkt dat ongeveer 18% van de zakjes toch nog minder dan
100 gram bevat. |
| |
|
|
|
|
| |
a. |
Bereken dit percentage nauwkeuriger:
geef twee decimalen. |
| |
|
|
|
|
| |
Neem aan dat inderdaad 18% een
gewicht van minder dan 100 gram heeft. Als je dan een steekproef
van 300 zakjes neemt dan is er een kans dat er in deze
steekproef minstens 60 zakjes zijn die minder dan 100 gram
wegen.
Bereken deze kans op twee manieren: |
| |
|
|
|
|
| |
b. |
Met de binomiale verdeling |
| |
|
|
| |
c. |
Als benadering met de normale
verdeling |
| |
|
|
|
|
| |
|
| 8. |
Iemand gooit een zuiver muntstuk een
even aantal keer en wil berekenen hoe groot de kans is dat
precies de helft van de keren "kop" verschijnt. |
| |
|
|
|
|
| |
a. |
Bereken deze kans als hij 20 keer
gooit exact. Geef je antwoord in 4 decimalen nauwkeurig. |
| |
|
|
| |
b. |
Bereken deze kans als hij 20 keer
gooit met een normale benadering. Geef je antwoord in 4
decimalen nauwkeurig. |
| |
|
|
|
|
| |
Het verschil tussen de antwoorden op
vraag a) en b) is niet zo groot. Het blijkt dat, als het aantal
keer gooien (n) groter wordt, dat dan het verschil tussen
de antwoorden steeds kleiner wordt. |
| |
|
|
|
|
| |
c. |
Leg uit waarom dat zo is |
|
|
|
|
 |
d. |
Bepaal met je GR vanaf welke n de normale benadering
minder dan 0,0001 verschilt met de exacte berekening. |
| |
|
|
|
|
| |
|
|
|
|
| 9. |
Van
alles worden tegenwoordig statistieken bijgehouden.
Op het WK voetbal 2002 werd bijvoorbeeld bijgehouden hoeveel
overtredingen er in een wedstrijd waren. De meeste overtredingen waren
er in de wedstrijd Japan -
Rusland, de minste bij Nigeria
- Engeland: "slechts"
19. Het blijkt dat het aantal overtredingen per wedstrijd bij
benadering normaal verdeeld is met een gemiddelde van 40 en een
standaarddeviatie van 12. |
| |
|
|
|
|
| |
a. |
Hoeveel
procent van de wedstrijden zal dan 62 of meer overtredingen hebben? |
| |
|
|
|
|
| |
Op 25
juni was de 1/8 finale tussen Nederland en Portugal qua aantal
overtredingen een sportief dieptepunt. Er werden zóveel overtredingen
gemaakt dat de kans op minstens dat aantal overtredingen vooraf gelijk
was aan (afgerond) slechts 0,1%. |
| |
|
|
|
|
| |
b. |
Hoeveel
overtredingen waren dat? |
|
|
| |
|
|
|
|
| |
Rugby
is een veel hardere maar ook veel eerlijker sport. Het aantal
overtredingen bij rugby is veel kleiner dan bij voetbal. Het blijkt dat
het aantal overtredingen in een rugbywedstrijd
alleen afhangt van de temperatuur! Hoe warmer, des te meer
overtredingen. Experts hebben het volgende model opgesteld: |
| |
|
|
|
|
| |
O
= 3,4T - 38,4 |
| |
|
|
|
|
| |
Deze
formule is gebaseerd op een aantal metingen met een gemiddelde
temperatuur van 19,8°C
en een standaarddeviatie van 3,2°C. |
| |
|
|
|
|
| |
c. |
Als de formule hierboven precies klopt, welk van
onderstaande klokvormen hoort dan bij het aantal overtredingen?
Geef een duidelijke uitleg. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
 10. 10. |
Je kunt een binomiaal experiment
benaderen door een normale verdeling met een gemiddelde van 84
en een standaarddeviatie van 8
Hoe groot is dan de kans op 84 successen? |
| |
|
|
|
|
 11. 11. |
Het aantal regendagen in een
maand is in een bepaald gebied normaal verdeeld met een
gemiddelde van 15.
Ga in deze opgave uit van een jaar met 12 maanden van 30 dagen.
Het blijkt dat de kans op minstens 19 regendagen in een maand
gelijk is aan de kans op precies 11 of 12 regendagen.
Hoe groot is dan de kans dat een jaar precies 3 maanden heeft
met 15 regendagen? Geef je antwoord in twee decimalen
nauwkeurig. |
| |
|
|
|
|
| |
|
|
|
|
 |
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|