complexe logaritmen


Logaritmen	© h.hofstede (h.hofstede@hogeland.nl)

Nou, dat moet niet al teveel moeilijkheden opleveren, zou ik zeggen. logaritmen hebben we ooit ingevoerd als inverse van machten en we weten intussen perfect door die regel van Euler hoe we moeten machtsverheffen. Dat moet ons zeker op het juiste spoor zetten wat betreft logaritmen. Verder willen we natuurlijk graag dat de rekenregels voor logaritmen die voor reële getallen gelden, ook voor complexe getallen blijven gelden.
De belangrijkste daarvan is:

lnab = lna + lnb

Het helpt weer enorm om een complex getal in zijn poolnotatie weer te geven.
Kijk maar:

ln(r • eⁱ^φ) = lnr + ln(eⁱ^φ) = lnr + iφ

Bij de laatste stap is gebruik gemaakt van het feit dat lnx en e^x elkaars inverse zijn.
Daar staan nu twee uitdrukkingen die we kennen (bedenk dat r een reëel getal is).

Er zijn echter twee dingen waar je om moet denken.....

1. Logaritmen van negatieve getallen.

Dat was bij de reële getallen onmogelijk, maar als je complexe antwoorden toelaat kan het ineens wél.
Bedenk dat -1 = e^iπ
Dan is dus ln(-1) = ln(eⁱ^π) = iπ
En automatisch is dan bijvoorbeeld ln(-5) = ln(-1 • 5) = ln(-1) + ln(5) = iπ + ln5

ln(-a) = ln(-1 • a) = ln(-1) + lna = ip + lna

2. ln(z) is meerwaardig.

Stel dat ln(z) = w met z en w beide complexe getallen.
Omdat ln(z) de inverse van e^z is, moet dan ook gelden z = e^w
Dus als we een w vinden die een oplossing van deze vergelijking is, dan hebben we ln(z) gevonden.
Maar het probleem is: Er zijn oneindig veel oplossingen voor w!!!

Kijk maar:
Stel dat we een w hebben gevonden zodat geldt z = e^w
Dan is e^{w + 2πi} = e^w • e^2πⁱ = e^w • 1 = e^w = z. Dus is ook w + 2πi een oplossing.
En op dezelfde manier zijn ook w + 4πi en w + 6πi enz. oplossingen.

ln(z) is bepaald op een aantal maal 2πi na.

Zodra je ergens opschrijft lnz = w moet je dus eigenlijk opschrijven lnz = w + k • 2πi
Dat meerwaardig zijn van ln(z) leidt soms tot vreemde dingen. Een voorbeeld staat in de verdieping hiernaast.

Wiskundigen lossen dit vervelende probleem op, door bijvoorbeeld af te spreken dat het imaginaire deel van ln(z) altijd tussen -π en π moet liggen. Dat noemen ze de hoofdwaarde van ln(z).

Maar dat geeft ook weer nadelen... zucht....

Stel dat je de functie f(z) = ln(z) uitrekent voor allerlei punten in het complexe vlak.
Dan wil je graag dat, als je z geleidelijk aan laat veranderen, dat dan ook ln(z) geleidelijk aan verandert, en niet zomaar rare sprongen maakt. Maar dat gebeurt met die hoofdwaarden wél.
Als je bijvoorbeeld z langzaam over een cirkel laat lopen en elke keer ln(z) uitrekent, dan vertoont die ln(z) als je de negatieve x-as passeert ineens een sprong van 2πi !
Hiernaast hebben we het complexe vlak plat neergelegd, en de waarde van het imaginaire deel van lnz boven of onder een punt getekend (de blauwe lijn) terwijl we dat punt de eenheidscirkel laten doorlopen.

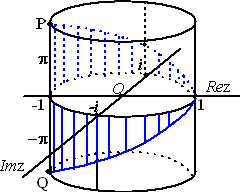Je ziet dat je, als je van de "bovenkant" naar -1 toeloopt dat je uitkomt in punt P, en vanaf de onderkant kom je in punt Q. Dus bij het passeren van -1 in het complexe vlak maakt het imaginaire deel van ln(z) een rare sprong van 2π.

Het is eigenlijk precies zoals bij de datumgrens op onze aarde. We willen graag dat het overal op aarde dezelfde datum is, maar tegelijkertijd weten we dat het naar het oosten toe later wordt en naar het westen vroeger. De enige oplossing is een rare sprong te maken!!

Bereken exact (je hoeft geen rekening te houden met het meerwaardig zijn van logaritmen; één oplossing is voldoende):

ln(2 - 2i√3)

ln√5 - ¹/₃πi

ln(2i) + ln(4i)

ln8 + πi

ln(-4)

ln4 + iπ

ln(-¹/_e)

iπ - 1

ln(4i - 4)

ln(4√2) + ³/₄πi

i • ln(i)

-¹/₂π

ln(3ie)

1 + ln3 + ¹/₂πi

ln(-5e²)

πi + 2 + ln5

Bij de reële logaritmen hebben we een formule geleerd om van grondtal te veranderen.
Dat was:

Deze formule geldt ook voor complexe getallen, dus kunnen we hem gaan gebruiken om logaritmen uit te rekenen met een complex grondtal.

Bereken ⁱlog i

1 natuurlijk

Bereken ⁴ⁱlog(e)

^-2/_{(iπ
+ 2ln4)}

Hoe groot is iⁱ?

Nou ja zeg! Wie wil dat nou weten?
i zelf was al zo moeilijk om te bevatten. En dan gaan we nu een complex getal tot de macht een complex getal nemen.
Dat levert vast iets verschrikkelijks op!!!
We kunnen ons al moeilijk iets voorstellen bij √-1 dus al helemaal niet bij (√-1)⁽^√-1) .
Wat is dat in vredesnaam?

Toch maar een poging: omdat e^0,5πi = i geldt ook:

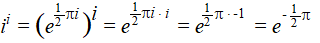Nou ja zeg! Dat is gewoon een reëel getal!
Uitrekenen geeft:

iⁱ = 0,207879576....

Geef toe: dat had je nooit verwacht! Ik ben zelf ook elke keer weer verbaasd......


formule van Euler			functies e^z en lnz

Bereken exact indien mogelijk, en anders in vier decimalen nauwkeurig:

i⁴ⁱ

e^-2^π

(iⁱ)ⁱ

-i

i^-i

e^0,5π

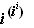cosa + i • sina
met a=¹/₂πe^-0.5^π

(2i)²ⁱ

cos(ln(4))•e^-π +
i • sin(ln4))•e^-π

i^√ⁱ

e^a cosa + ie^asina
met a = ¹/₄π√2

Je hebt in de vorige opgave ontdekt dat (2i)²ⁱ geen reëel getal is.
Voor welke n is (ni)ⁿⁱ wél een reëel getal? Geef je antwoord(en) in drie decimalen nauwkeurig.

n • lnn = k • π
n = 1, 2.926..., 4.305... enz.