complexe integralen


	© h.hofstede (h.hofstede@hogeland.nl)

Complex Integreren.

Je kunt je vast nog wel herinneren dat een integraal eigenlijk niets anders was dan een som. Het begon als oppervlakte onder een grafiek met allemaal rechthoekjes met breedte dx en hoogte f(x).

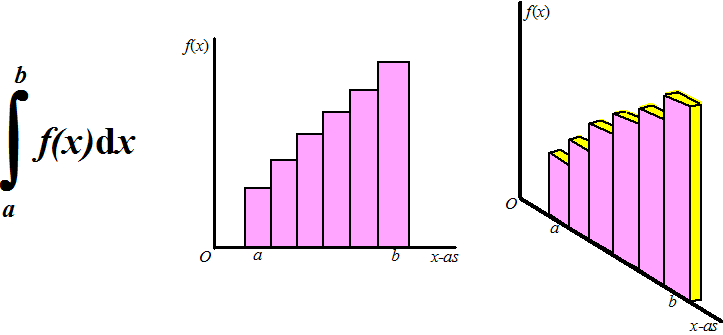Bedenk goed wat hier gebeurt: eigenlijk tel je een heleboel keer f(x) voor allemaal verschillende x bij elkaar op. Als we dat principe naar complexe getallen willen uitbreiden, dan stuiten we direct op een groot probleem.

Kijk, dat zit hem hier in: die x-en liggen in dit geval netjes naast elkaar geordend op een rechte lijn: de x-as. Dat doen reële getallen nou eenmaal wel, maar bij complexe getallen is dat nogal anders:

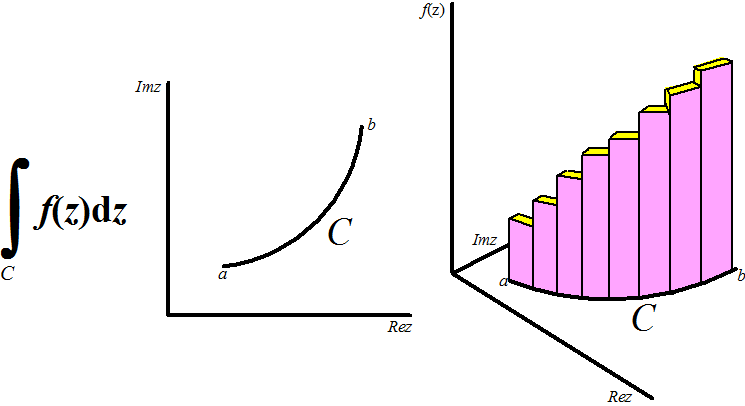De grenzen a en b zijn nu complexe getallen, dus die liggen in het complexe vlak (en niet op de x-as). Je moet dat hele vlak beschouwen als een x-as!!! Maar dat betekent dat je een route van a naar b op allerlei verschillende manieren kunt maken. Hierboven staat één zo'n route C in het complexe vlak getekend, en rechts zie je dat je langs zo'n route C weer allemaal functiewaarden moet optellen (trouwens die functiewaarden f(x) zijn rechts als hoogtes van staafjes weergegeven, maar dat zijn eigenlijk natuurlijk óók weer complexe getallen, dus die staafjes, dat klopt niet helemaal: is alleen bedoeld om duidelijk te maken dat je langs route C allemaal "functiewaarden" moet optellen.

Een erg belangrijke vraag is natuurlijk:

"Levert elke route C dezelfde som op?"

Zo'n integraal langs een bepaalde route C heet een lijnintegraal.

Hoogste tijd om eens zo'n lijnintegraal uit te rekenen. Houd daarbij goed in gedachten dat alle regels die we al van reële getallen over integreren weten ook nu moeten blijven gelden.

Een lijnintegraal berekend.....

We gaan in het complexe vlak de integraal uitrekenen van de functie
f(z) = z² tussen de punten z = 1 en z = i (A en C hiernaast)
Daarvoor kunnen we dus verschillende routes kiezen.......

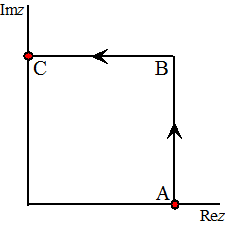
Neem de route A → B → C hiernaast.
De integraal kun je dan splitsen in een integraal van A naar B en een integraal van B naar C.

Als z = a + bi dan geldt op traject AB dat z = 1 + bi
Dan is z² = 1 + 2bi - b² en dz = idb. Verder loopt b van 0 tot 1
Dat geeft:

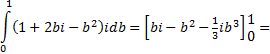= i - 1 - ¹/₃i = ²/₃i - 1

Op traject BC geldt dat z = a + i
Dan is z² = a² + 2ai - 1 en dz = da. Verder loopt a van 1 naar 0 (let op de volgorde)
Dat geeft:

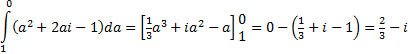De totale lijnintegraal van f(z) = z² op de route A®B®C is dan (²/₃i - 1) + (²/₃ - i) = -¹/₃ - ¹/₃i

Een alternatieve route....
In plaats van de route A→B→C hadden we natuurlijk net zo goed van A naar C kunnen gaan via de kwartcirkel hiernaast.

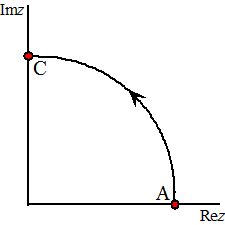
Op die kwartcirkel is z = re^iφ met r = 1 dus z = e^iφ
Dan is z² = e^2iφ en dz = ie^iφ dφ. Verder loopt φ van 0 tot ¹/₂π
Dat geeft in één keer:

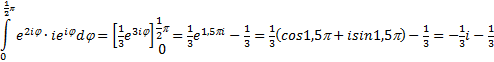Nou daar komt dus mooi hetzelfde uit. Zullen we dan maar concluderen dat dat altijd zo is?
Dat zou wel handig zijn, want dan kunnen we het tenminste hebben over "DE" integraal van A naar B.

Laten we het nog een keer proberen via de directe rechte lijn AC.
Op die route is z = a + (1 - a)i (met a van 1 naar 0)
z² = a² + 2a(1 - a)i + (1 - 2a + a²) • -1 = a² + 2ai - 2a²i - 1 + 2a - a² = 2ai - 2a²i - 1 + 2a
dz = da - ida = da(1 - i)
Dat geeft voor de integraal:

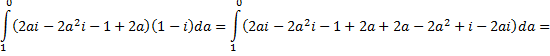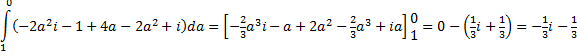Nou ja zeg! Alweer hetzelfde. Ik geloof het intussen wel.

De waarde van de lijnintegraal is onafhankelijk van de gekozen route!

(Voor het bewijs van deze toch wel revolutionaire stelling moet je even wachten tot de volgende les, waar we de eerste integraalstelling van Cauchy behandelen).

Wacht, daar moet ik toch even een kleine "ja maar" aan toevoegen:

De waarde van de lijnintegraal is onafhankelijk van de gekozen route!
...... JA MAAR..... alleen voor "nette" functies!!!!

Daarmee bedoel ik natuurlijk analytische functies die voldoen aan de CR-vergelijkingen van de vorige les.
Hier zie je een voorbeeldje van wanneer dat wel en wanneer dat niet zo is.

Hier is het wél zo:

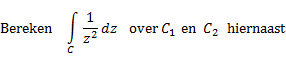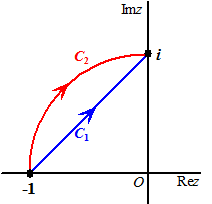Op C₁ geldt z = a + bi met b = a + 1 dus z = a + (1 + a)i.
Dat is z = a(1 + i) + 1 dus dz = (1 + i)da
Daarbij loopt a van -1 naar 0.

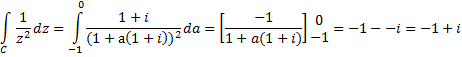Op C₂ geldt z = eⁱ^φ dus ¹/_z² = e^-2iφ en dz = ieⁱ^φdφ
φ loopt van π tot ¹/₂π dus de integraal wordt:

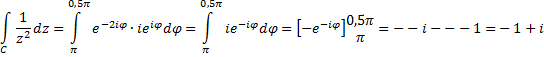Die zijn inderdaad mooi hetzelfde.

.... Maar hier is het níet zo:

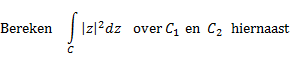Op C₁ is: z = a + (1 + a)i dus | z |² = a² + (1 + a)² = 2a² + 2a + 1

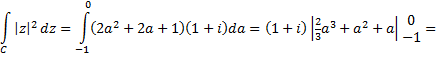= (1 + i) • (0 - - ²/₃) = ²/₃ + ²/₃i

Op C₂ geldt z = eⁱ^φ dus | z |² = 1 en dz = ieⁱ^φdφ

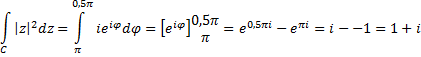Dat de integralen over die twee verschillende routes deze keer niet gelijk zijn ligt natuurlijk aan het feit dat deze tweede functie f(z) = | z |² niet analytisch is.......

Neem aan dat de stelling bij de volgende opgaven steeds wel geldt. Dus mag je daar elke keer zelf een handige route kiezen om de integraal te berekenen.

ÒPGAVEN

Bereken de volgende complexe integralen:

De integraal van f(z) = 2z + 1 van 2i naar 1 + i

5 + i

De integraal van f(z) = lnz van 1 naar i

1 -¹/₂π - i

Bereken de integraal van f(z) = z van -5 naar -3 + 4i op twee manieren:
I: met als route twee rechte lijnstukken
II: met als route een cirkeldeel.

-16 - 12i

De integraal van f(z) = z² van ¹/₂ + 2i naar 1 + i kun je vrij eenvoudig berekenen door een route langs twee rechte lijnstukken te nemen.

Bereken deze integraal via punt P hiernaast

^31/₂₄^{+
17/}₆i

je kunt de integraal ook berekenen door als route de groene kromme hiernaast " y = ¹/_x " te nemen.
Dat is in het complexe vlak dus de lijn Imz = ¹/_Rez.

Bereken de integraal volgens deze alternatieve route.

^31/₂₄^{+
17/}₆i

Hiernaast zie je het complexe vlak met daarin twee routes van 1+i naar 2+4i. De blauwe route is eenvoudig (evenwijdig aan de assen), en de rode route loopt langs wat in het reële vlak de parabool y = x² zou zijn.

Neem f(z) = 6z² + 2iz

Bereken de integraal van deze functie langs de blauwe route.

-186 - 48i

Laat zien dat je deze integraal ook kunt berekenen door "gewoon" complexe getallen te primitiveren, alsof het reële getallen zijn.

Bereken de integraal langs de rode route.