| De Mooie Oplossing: |
|
|
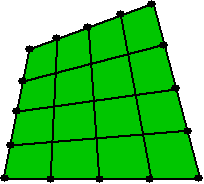
Verdeel alle vier de zijden van de vierhoek in
vieren en verbind de punten op overstaande zijden met elkaar.
Dat geeft 16 gebieden.
Als je nu 4 gebieden kiest die niet in dezelfde rij of kolom
zitten is de oppervlakte precies een kwart van het geheel!
Deze methode geldt trouwens voor elk aantal gebieden; niet
alleen bij 4. |
 |
| Hoe is dat te zien? In
drie stappen ! |
|
|
|
STAP 1
Elke vierhoek ABCD heeft de volgende prettige eigenschap:
Stel dat P en Q overstaande zijden in dezelfde verhouding
verdelen, en R en S ook, dan verdelen PQ en RS elkaar óók in
diezelfde verhouding.
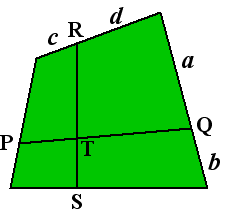
In de figuur hiernaast betekent dat, dat PT/TQ
= c/d en RT/TS
= a/b
Bewijs:
Als ABCD een parallellogram is, is het bewijs triviaal want
dan zijn er in de figuur alleen maar gelijkvormige delen.
Als ABCD géén parallellogram is, dan maken we dat ervan. |
 |
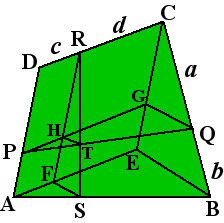
Trek AE evenwijdig aan DC en CE
evenwijdig aan DA.
Verdeel parallellogram AECD in vier kleinere parallellogrammen
door RF en PG te tekenen.
Verder is HT evenwijdig aan FS.
Nu zijn er veel parallellogrammen te zien waarvan de zijden in
gelijke verhoudingen worden verdeeld. En ook een aantal
driehoeken waarvan de zijden in gelijke verhoudingen worden
verdeeld door een lijn die dus evenwijdig aan de derde zijde is:
AF/FE = c/d
= AS/SB dus in driehoek AEB is FS
evenwijdig aan EB.
CG/GE = a/b
= CQ/QB dus in driehoek CEB is GQ
evenwijdig aan EB.
Kortom: HT, FS, EB en GQ zijn allemaal evenwijdig.
Maar dan is hoek HPT gelijk aan hoek GPT dus ligt T op PQ.
HT is evenwijdig aan FS dus in driehoek RFS verdeelt HT de twee
zijden in gelijke delen; ofwel:
RH/HF = a/b
= RT/TS
Het zelfde verhaal met driehoek GPQ geeft PH/HG
= c/d
= PT/TQ
|
 |
|
Daarmee is stap 1 bewezen.
Belangrijk gevolg:
|
| De lijnen in de
figuur helemaal bovenaan verdelen elkaar in
gelijke stukken. |
|
|
|
|
| STAP 2 |
|
|
|
Verdeel nu het parallellogram in m
bij n gebieden.
Dan delen de lijnen elkaar in gelijke stukken, zoals we
hierboven zagen.
Laten we beginnen met twee gebieden.
Omdat P, Q, R en S de middens van de zijden zijn, zijn TP,
TQ, TR en TS de zwaartelijnen van de driehoeken TDA, TCB, TDC en
TAB. Die delen de driehoeken dus in twee gelijke oppervlakten.
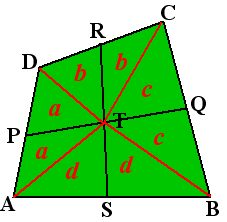
Voor de oppervlaktes in de figuur hiernaast geldt:
TPDR + TSBQ = a + b + c + d =
PAST + RTCQ
|
 |
Belangrijk tussenresultaat:
|
| Als we de middens van
de zijden verbinden zijn de gele
en de blauwe oppervlakten gelijk! |
|
 |
|
|
|
|
|
| STAP 3 |
|
|
|
| Naar meer gebieden: de
gelijkheids-ziekte breidt zich uit. |
Beschouw meer gebieden, en noem
hun oppervlaktes a, b, enz.
Begin met a + g = f + b
Dan geldt ook f + l = g + k,
en als we deze twee vergelijkingen bij elkaar opstellen vinden
we
a + g + f + l = f + b +
g + k ofwel a + l = b +
k
Nog een keer hetzelfde: k + q = p
+ l optellen bij de vorige vergelijking geeft:
a + l + k + q = b + k
+ p + l ofwel a + q = b
+ p
Zo breidt de ziekte zich naar boven uit.
En ook naar rechts gebeurt uiteraard precies hetzelfde:
a + g = f + b en b
+ h = g + c telt op tot a + g
+ b + h = f + b + g + c
ofwel a + h = f = c.
Kies vier hoekpunten van een willekeurige vierhoek uit de
figuur. Dan zijn de oppervlaktes van de parallellogrammen in de
vierhoeken kruislings opgeteld aan elkaar gelijk.
|
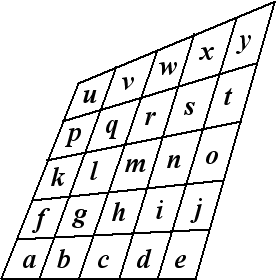
|
|
|
En dat geeft dan eindelijk de
mogelijkheid een vierhoek in gelijke stukken te verdelen
Dat gaat als volgt.
Stel dat we n oppervlaktes hebben gekozen die niet in
dezelfde rij of kolom liggen. (zie hiernaast). Dan gaan we
bewijzen dat de oppervlakte van deze n gebieden samen
gelijk is aan de oppervlakte van de hoofddiagonaal (van
linksboven naar rechtsonder van de figuur).
Loop gewoon alle vakjes van de hoofddiagonaal af. Als het vakje
bij onze verzameling hoort gaan we door naar het volgende vakje
van de hoofddiagonaal.
Als dat niet zo is voor vakje X van de hoofddiagonaal, zoeken we
de vakjes P en Q in dezelfde rij en in dezelfde kolom als X die
wél bij onze verzameling horen. Daarna noemen we Y het vakje
dat met P, Q en X een vierhoek maakt, en tot slot vervangen we P
en Q door X en Y. Daarmee blijft de oppervlakte gelijk. Een
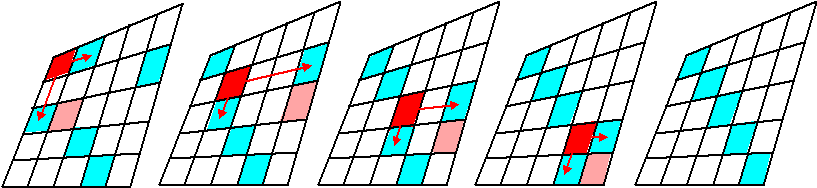
stripverhaal van dit proces zou er zó uitzien (het
oorspronkelijke gebied is blauw, en we veranderen het stap voor
stap naar de hoofddiagonaal toe): |
|
|
 |
|
|
Zo zien we dat de oppervlakte van
ons oorspronkelijke gebied gelijk is aan de oppervlakte van de
hoofddiagonaal.
Omdat dat geldt voor elk willekeurig gebied (met vakjes in
verschillende rijen en kolommen) is de oppervlakte ook precies
gelijk aan 1/n.
Daarmee is dan eindelijk onze methode bewezen. |
|
|
| 2.
Een vierhoek vierendelen! |
|
|
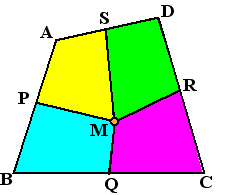
Het lijkt een eenvoudiger probleem
dan het vorige maar is het niet!
Zoek punt M in een (convexe) vierhoek zodat de lijnen van M naar
de middelpunten van de zijden de vierhoek in vier stukken met
gelijke oppervlakte delen.
Toch is de oplossing weer van verrassende schoonheid.....
|
 |
 |
|
|
|
|