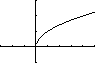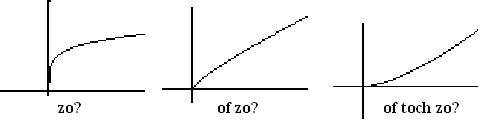grafieken randpunten


Wortelgrafieken.	© h.hofstede (h.hofstede@hogeland.nl)

Op een zondagmiddag heb ik even niets te doen, dus ga ik lekker wat wiskunde bedrijven. Ik besluit de grafiek van y = √x eens te gaan plotten, want dat heb ik nog nooit gedaan. (Try before you die?)
Dat levert me de grafiek hiernaast op.
Nou ja, zeg!
Stom apparaat!!!

Mijn TI-83 weigert zomaar om de grafiek links van de y-as te tekenen.
Ik tik een paar keer op het venstertje maar er gebeurt niets! Aan de batterijen kan het ook niet liggen, want die heb ik net vervangen.....

Wat is hier aan de hand?

Als ik weer wat gekalmeerd ben, bedenk ik me dat dat natuurlijk geen kwade opzet van mijn TI-83 is. Kennelijk kan het apparaat gewoon niet van elke x de wortel trekken.
Aan de grafiek te zien lukt het niet bij wortels van een negatief getal.
Ach natuurlijk!
Dat is ook wel logisch eigenlijk.
Het is namelijk onmogelijk om de wortel van een negatief getal te trekken!

Waarom is dat zo?

Dat is simpel te zien met wat wiskundigen noemen een "bewijs uit het ongerijmde". Gaat zo:
• Stel dat bijv. √(-5) wél zou kunnen.
• Dan is er dus een getal x zodat geldt x² = -5
• Maar dat kan niet, want een getal in het kwadraat is altijd positief.
• Met onze aanname komen we uit op onzin, dus kan die niet kloppen, dus bestaat √(-5) niet.

Conclusie: de grafiek van y = √x bestaat niet voor x < 0.
Het laatste punt waar hij nog wel bestaat is bij x = 0 zélf (want √0 = 0 kan nog nét). Daar stopt de grafiek abrupt.
Zo'n punt waar de grafiek ineens stopt noemen we een RANDPUNT.

Randpunten bij ingewikkelder vergelijkingen

Die kun je heel simpel vinden:
Als je een vergelijking hebt waar ergens een wortel in staat, dan kijk je alleen naar het deel onder de wortel. Als dat deel nul is, dan kan de wortel nog nét en daar heb je dan een randpunt.

Voorbeeld: Geef de coördinaten van het randpunt van de grafiek van f(x) = 2x³ + √(3x - 21) + 15
Oplossing: De wortel wordt genomen van 3x - 21. Dat is nul als x = 7 dus daar zal een randpunt zitten.
f(7) = 2 • 7³ + √(3• 7 - 21) + 15 = 701 dus het randpunt is (7, 701).
Aan de kant waar 3x - 21 > 0 bestaat de grafiek wel, en aan de kant waar 3x - 21 < 0 bestaat de grafiek niet.
Ofwel: het domein van deze functie is [7, →〉

1. Geef de coördinaten van het randpunt van de volgende functies:

f(x) = √(4 - 2x)

(2, 0)

f(x) = 7x + 2√(x - 3)

(3, 21)

f(x) = 2 - 3√(x + 5)

(-5, 2)

f(x) = 4x - √(4x - 1)

(¹/₄, 1)

f(x) = 6√(3x + 9)

(-3, 0)

f(x) = √(9 - x²)

(±3, 0)

2. Geef een mogelijke formule bij de volgende grafieken:

a. Een grafiek met een randpunt bij x = 5 en die bestaat voor x > 5.

b. Een grafiek met een randpunt (-2, 4).

c. Een grafiek met een randpunt (1,3) en die bestaat voor x > 1.

d. Een grafiek met een randpunt bij x = 8 en die bestaat voor x < 8

e. Een grafiek met een randpunt (5, -3) en die bestaat voor x < 5.

Hierboven staat het vooraanzicht van een grote loods.
De wanden ervan zijn ontworpen volgens de functies h = 1,9√x en h = 1,9√(18 - x)

Welke functie hoort bij welke wand?

1,9√x links

Hoe breed is de loods?

18 m

Hoe hoog is het hoogste punt van de loods?

5,7 m

Men wil een tweede loods bouwen die 12 meter breed wordt, en op het hoogste punt 4 meter hoog.
Deze loods moet ook de vorm van een wortelgrafiek krijgen.

Geef mogelijke vergelijkingen voor de wanden van deze loods.

²/₃√(6x)
²/₃√(6x - 72)

Hoe loopt de grafiek in de buurt van zo'n randpunt?

De grafiek van √x loopt naar de oorsprong toe, maar hoe? Is dat heel steil of onder 45º of juist bijna horizontaal?

Je kunt dat natuurlijk gewoon onderzoeken door de helling vlakbij (0,0) te gaan berekenen. in de volgende tabel is steeds verder "ingezoomd" naar de oorsprong en elke keer de helling berekend.

tussen de x-waarden:	0 en 1	0 en 0,1	0 en 0,01	0 en 0,001	0 en 0,0001	0 en 0,00001	........
helling;	1	3	10	32	100	320

Je ziet dat de helling snel steeds groter en groter wordt. De grafiek loopt dus zoals in het linkerplaatje hierboven: "langs de y-as.

4.	Hiernaast staat een deel van de grafieken van y = 1 + √x en y = √(x + 1) Zoals je ziet gaan ze beiden door (0,1) Hoe kun je in één oogopslag zien welke de grafiek van y = 1 + √x is?

5.	Hiernaast staan in één figuur de grafieken van y = √x en y = x² getekend. Wat hebben deze grafieken met elkaar te maken? Hoe ontstaat de ene grafiek uit de andere? De grafiek van y = x² heeft in de oorsprong een top. Hoe kun je met dat gegeven de helling van de grafiek van y = √x beredeneren?

Examenvraagstuk HAVO Wiskunde B 2022-I
(met de afgeleide)

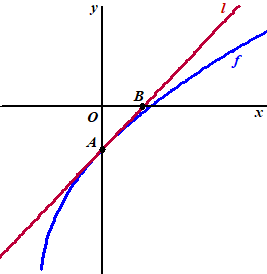
De functie f is gegeven door f(x) = -8 + 2√(3x + 9).
De grafiek van f snijdt de y-as in het punt A. De lijn l raakt de grafiek van f in A. De lijn l snijdt de x-as in het punt B. Zie onderstaande figuur.

Toon dat OA = OB

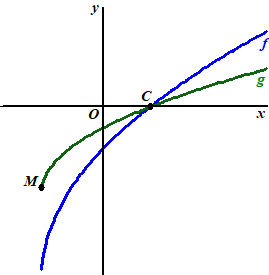
De grafiek van de functie g ontstaat uit de grafiek van f door middel van een vermenigvuldiging ten opzichte van de x-as met een positieve factor a. Het punt M is het randpunt van de grafiek van g en het punt C is het snijpunt van de grafieken van f en g met de x-as. Zie onderstaande figuur. De lengte van het lijnstuk MC is 6²/₃.

Bereken de exacte waarde van a

a = 0,5