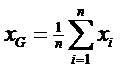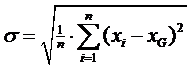Nieuwe pagina 1

© h.hofstede (h.hofstede@hogeland.nl)

Formules voor de standaarddeviatie.

Laten we al onze metingen nummeren en ze x₁, x₂, x₃, .... enz. noemen.
Verder geven we het gemiddelde aan met x_G en het totaal aantal metingen met n.
Tot slot hoop ik dat je de notatie Σ voor de som van een aantal getallen kent. Als dat niet zo is moet je eerst deze les lezen.
Goed, dan hoop ik dat je het volgende met me eens bent:

MEE EENS?
Als je dat niet met me eens bent kun je nu beter met deze les stoppen, of alsnog die les over de somnotatie eerst bestuderen....
Goed, voor wie er nog over zijn gaan we nu een formule voor de standaarddeviatie maken.

We berekenden de standaarddeviatie in een aantal stappen die we nu gaan samenvatten in een formule.

•

Bereken het gemiddelde x_G

•

Bereken de afstand van elke meting tot het gemiddelde: die afstand is x_i - x_G (We maken ons even niet druk over het feit of dat positief of negatief is, waarom niet; dat zie je zo wel).

•

Neem die afstanden in het kwadraat: dat geeft (x_i- x_G)² (Je ziet dat plus/min teken er inderdaad niet toe doet)

•

Tel al die kwadratische afwijkingen bij elkaar op:

•

Deel door het totaal aantal metingen:

•

Neem daar tenslotte weer de wortel van:

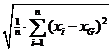En daar heb je al een formule voor de standaarddeviatie:

Een andere variant.

Sommige slechte boeken werken deze formule nog verder uit. Die schrijven dan :

Daar staan nu drie termen waarvan je de tweede en derde kunt vereenvoudigen.
De tweede term: de som van alle x_i is gelijk aan n • x_G. (dat is nou eenmaal een eigenschap van het gemiddelde)
De derde term: onder die som staat een constante, dus daar staat n keer hetzelfde, dus dat is gewoon n • x_G²
Samen geeft dat dan:

Voor de standaarddeviatie moet daar eerst nog weer een factor ¹/_n voor en dan de wortel nemen, dus dat geeft:

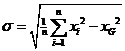Die eerste term onder dat wortelteken is gelijk aan het gemiddelde van alle x² (immers je telt ze op en deelt door het aantal). Daarom kun je de formule nóg eenvoudiger zó opschrijven:

"(gemiddelde van alle kwadraten) - (kwadraat van het gemiddelde)"
Klinkt lekker simpel toch?

En toch is deze formule meestal minder goed. Dat zit hem in het volgende.
Kijk, als je de standaarddeviatie met een computer/rekenmachine uitrekent dan doet het er niet toe welke formule je gebruikt. Je doet het toch immers niet zelf.
Maar als je de standaarddeviatie met de hand uitrekent, dan is die tweede formule nogal gevoelig voor afrondingen. Vooral een afronding van het gemiddelde (dat zul je meestal eerst uitrekenen) beïnvloedt de zaak nogal.

Stel dat je een klein foutje f in het gemiddelde hebt gemaakt en dus in plaats van x_G de waarde x_G + f gebruikt.

Dan geeft de oorspronkelijke formule voor de standaarddeviatie

Bij de laatste stap is gebruikt dat de som van alle x_i - x_G samen NUL is (dat is nou eenmaal een eigenschap van het gemiddelde).
Waar verschijnt de fout f ? Alleen in de term met nf²
De fout in de standaarddeviatie ten gevolge van ons foutje f in het gemiddelde is dus nf²

De "mooiere" tweede formule geeft:

Waar komt hier de f tevoorschijn?
In de term 2x_Gf en die hoeft zeker niet nul te zijn. Als het gemiddelde groot is kan dit een erg grote fout opleveren.
De fout in de standaarddeviatie ten gevolge van ons foutje f in het gemiddelde is dus 2x_Gf + nf²

Klein voorbeeldje.

Stel dat we de drie metingen x₁ = 84 en x₂ = 86 en x₃ = 87 hebben en daar de standaarddeviatie van willen berekenen.
Het gemiddelde is dan 85²/₃ maar stel dat we dat per ongeluk afronden naar 85,667

methode 1.
geeft voor de kwadraten van de verschillen dan (84 - 85,677)² en (86 - 85,677)² en (87 - 85,667)²
opgeteld geeft dat 4,666667 en gemiddeld is dat 1,555555667
dat geeft voor de standaarddeviatie √( 1,555566667) = 1,24722....

methode 2.
(x_G)² = 85,667² = 7338,834889
(x²) is achtereenvolgens 84² en 86² en 87² en het gemiddelde daarvan is 7340,333333
Het verschil is 7340,333333 - 7338,834889 = 1,498444
Neem daar weer de wortel van en je hebt σ = 1,224109....
Dat scheelt nogal!

De werkelijke s was overigens 1,247219....