De verbindingsmatrix.

© h.hofstede (h.hofstede@hogeland.nl)
       
De verbindingsmatrix (V) van een graaf is een matrix met daarin enen en nullen die aangeven welke punten van de graaf met elkaar verbonden zijn (1 = verbonden, 0 = niet-verbonden).
Als een graaf  k  knooppunten heeft, dan is de verbindingsmatrix dus altijd een k ×  k matrix  (VAN elk knooppunt NAAR elk knooppunt). Zo'n matrix noemen we een vierkante matrix, maar dat had je zelf waarschijnlijk ook nog wel verzonnen.
Hieronder zie je een graaf met rechts de bijbehorende verbindingsmatrix.
       

       
Misschien zijn een paar dingen je al opgevallen:
       

•

 Er staat voor de matrix : "naar"  en boven de matrix  "van",  maar dat maakt natuurlijk niet uit; als er een verbinding van A naar B is, is er ook eentje van B naar A. Deze matrix V is symmetrisch in de diagonaal. Omdat we zo meteen ook grafen met éénrichtingsverbindingen gaan bekijken (waar "VAN" en "NAAR" wél van belang zijn), staan ze er nu ook alvast.

•

 De verbindingsmatrix V geeft alleen maar aan óf de knooppunten verbonden zijn. Bij gewogen verbindingslijnen zijn de wegingen niet terug te vinden in V. Als je dat wél wilt kun je in plaats van een 1 natuurlijk het gewichtsgetal in de matrix zetten. In dat geval noemen we het niet meer de verbindingsmatrix (V), maar de wegenmatrix (W). In zo'n wegenmatrix kunnen ook éénrichtingsverbindingen zijn weergegeven. De matrix is dan niet meer symmetrisch. Zet in dat geval altijd "van" voor de matrix en "naar" er boven. Als de gewichten echte afstanden zijn dan wordt zo'n wegenmatrix W ook wel een afstandenmatrix (A) genoemd.
       
Meerstapsverbindingen.
       
Omdat zo'n verbindingsmatrix vierkant is, kun je hem altijd met zichzelf vermenigvuldigen.
Net als bij getallen noteren we V • V  als V2.  In bovenstaand voorbeeld geeft dat:
       

       
De vraag is natuurlijk:  "Wat stelt deze V2 nou vóór?"  "Wat moeten we ermee?" "Waarom is dit interessant?"
Laten we daarom proberen te achterhalen waar een getal van V2 vandaan komt.  Neem als voorbeeld die 2 in de derde rij en de tweede kolom:
       

       
Die 2 ontstond door de derde rij van V te vermenigvuldigen met de tweede kolom (groen met paars). Zoals je ziet is dat  1 • 1 + 0 • 0 + 0 • 0 + 0 • 0 + 1 • 1. En dat wordt 2 omdat er twee keer 1 • 1 in voorkomt.
Die eerste 1 • 1   komt van: (verbinding van C naar A) • (verbinding  van A naar B)
Die tweede 1 • 1 komt van: (verbinding van C naar E) • (verbinding van E naar B) 
Daar staan dus precies de twee routes C → A → B  en  C → E → B aangegeven: dat zijn alle routes om in twee stappen van  C naar B te komen! We noemen dat het aantal tweestapsverbindingen van C naar B.
Zo zie je in V2 ook bijvoorbeeld dat er 3 manieren zijn om van A in A te komen. In de graaf zie je ook direct dat het gaat om  de routes A → B → A en A → C → A en A → E → A.
       

V2  geeft het aantal tweestapsverbindingen
       
En ook als je een wegenmatrix W met gewogen verbindingen gebruikt geldt nog steeds dat W2 het aantal tweestapsverbindingen geeft, tenminste als in W het aantal routes staat aangegeven (niet als er iets anders als "kilometers" of zo staat).

Op dezelfde manier (als je het niet gelooft, dan ga je het zelf maar na) stelt V3  het aantal driestapsverbindingen voor, en V4 het aantal vierstapsverbindigen, enz.
In het algemeen:
       

Als matrix M het aantal verbindingen tussen de knooppunten van een graaf geeft,
Dan geeft Mn het aantal n-stapsverbindingen.
       
Dus wil je bijvoorbeeld weten op hoeveel manieren je in bovenstaande graaf in 5 stappen van B in E kunt komen, dan bereken je gewoon eventjes V5 .
Nou ja....eventjes......
Dat is nogal een werk.  Daarom wordt het nu hoog tijd onze GR in te schakelen voor dit "vieze werk".
       
Matrices in de GR
       
Je kunt matrixberekeningen met je TI uitvoeren. Als voorbeeld zal ik V5 van bovenstaand voorbeeld gaan berekenen. Dat gaat op de volgende manier.

 
Druk eerst op 2nd MATRIX  en kies 1: [A]  en EDIT en dan ENTER

Dan kun je boven in het scherm de afmetingen (rij × kolom) van de matrix invoeren.
In dit geval 5 × 5.
Vervolgens kun je de hele matrix invoeren. Door steeds een element in te voeren en dan op ENTER te drukken loopt je rekenmachine de matrix rij voor rij langs.
 

Al je klaar bent druk je op 2nd  QUIT
V is nu ingevoerd als matrix A in je rekenmachine.
V5  bereken je nu als volgt:
2nd  MATRIX  1:[A] 5 × 5   ENTER
[A]^5

Door naar rechts te scrollen krijg je alle elementen van V5 in beeld.
De conclusie is:

 
Daarin zie je dat er 38 manieren zijn om in vijf stappen van B naar E te gaan (tweede kolom, vijfde rij).
       
OPGAVEN
   
1. Van een graaf is het kwadraat V2  van de verbindingsmatrix gegeven door:
 

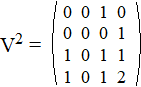  Teken een mogelijke graaf die hieraan voldoet.
   
2. examenvraagstuk HAVO wiskunde A, 1990.

De dieren in een gebied zijn voor voedsel van elkaar afhankelijk. Soort A eet bijvoorbeeld soort B. Men zegt in dat geval dat de voedselstroom van A naar B gaat. Bij meerdere diersoorten kunnen die voedselstromen een web vormen:  het zogenaamde voedselweb. Voor 8 diersoorten is de informatie over het bijbehorende voedselweb in de matrix W hiernaast gegeven.

Kolom A en rij G bestaan uit louter nullen
       
  a. Wat betekent dit voor deze diersoorten?
       
  Er gaan voedselstromen van G naar B en van B naar A. We noemen dit de keten  G → B →  A
       
  b. Wat is de langste voedselketen die in dit web voorkomt?
         
  Twee dieren zijn elkaars concurrent als ze een gemeenschappelijke prooi hebben.
         
  c. Welke paren concurrenten zijn er?
         
  Er is een giftige stof in het milieu terechtgekomen. Sommige diersoorten nemen dat gif op. Dat wordt in hun lichaam niet afgebroken zodat hun eters het ook binnenkrijgen, en het weer kunnen doorgeven. Ongeacht welke diersoort het gif het eerste binnenkrijgt, uiteindelijk bereikt het gif diersoort A.
         
  d. Toon dat aan.    
         
  Het is mogelijk van dit voedselweb een graaf te tekenen die er uitziet als hiernaast.

       
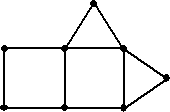  e. Geef in deze figuur de soorten A tm H en de richtingen van de voedselstromen aan.
         
  Als je W2, W3, W4 enz. gaat berekenen dan krijg je op een gegeven moment een matrix met alleen nog maar nullen.
         
  f. Leg met de graaf van vraag e) uit waarom dat zo is, en leg ook uit vanaf welke macht er alleen nog maar nullen zullen zijn.
         
3. Op het mini-schaakbord hiernaast staat een loper.  Een loper is een schaakstuk dat bij een zet diagonaal verplaatst mag worden, zover je maar wilt. Een loper in A zou bijvoorbeeld naar C of E kunnen.
De loper staat in het begin op veld B.
Iemand doet vier volledig willekeurige (maar wel toegestane) zetten met de loper.

Bereken met matrixvermenigvuldiging hoeveel mogelijke manieren er zijn om in vier zetten van veld B weer naar veld B te gaan.

         
4. Een klein jongetje probeert zijn gebruik van LEGO-blokjes wat wiskundig op orde te brengen. Hij onderscheid voor het bouwen van allerlei dingen grote blokjes en kleine blokjes en dakblokjes.
Voor het bouwen van een toren zijn  60 kleine blokjes en 20 grote blokjes en 15 dakblokjes nodig.
Voor het bouwen van een muur zijn 15 kleine blokjes en 48 grote blokjes nodig.
Voor het bouwen van een kasteel zijn 4 muren, 3 torens en nog 10 dakblokjes nodig.
         
  a. Zet deze gegevens in een 6 × 6 matrix W (zet bij de kolommen "voor het maken van"" en bij de rijen "is nodig")
         
  b. Bereken W2 en leg uit wat de getallen in de laatste rij van deze matrix voorstellen.
         
5. examenvraagstuk HAVO wiskunde A, 1994.
         
  Hieronder zie je een deel van de voedselketen van vogels voor de kust van Long Island (VS). Zo zie je bijvoorbeeld dat een voorn plankton en waterplanten eet. De voorn wordt onder andere door de ijsvogel gegeten.
         
 

         
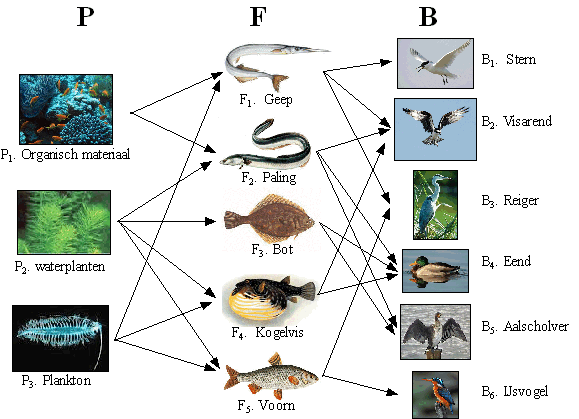  Stel dat er sprake is van een verhoging is van de hoeveelheid vergif in de waterplanten. Neem aan dat alleen de aangegeven planten en dieren gegeten worden. Met het voedsel wordt ook het vergif doorgegeven.
         
  a. Mag je een verhoging van de hoeveelheid vergif bij alle genoemde vogels verwachten? Licht je antwoord toe.
         
  Het is mogelijk bovenstaande voedselketen weer te geven met behulp van matrices. De voedselstromen van P naar F zijn in matrix M weergegeven.
         
 

         
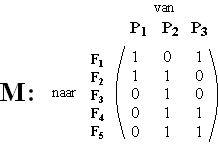  Een 1 in de matrix betekent dat de één als voedsel dient voor de ander en een 0 geeft aan dat de één niet door de ander wordt gegeten. Zo betekent bijvoorbeeld het getal 1 linksboven in de matrix dat P1 door F1 wordt gegeten en het cijfer 0 linksonder dat P1 niet door F5 wordt gegeten.
         
  b. Maak een dergelijke matrix N die de voedselstromen van F naar B weergeeft.
         
  c. Vermenigvuldig matrix N met matrix M.
         
  d. Wat is de betekenis van de getallen in de productmatrix van vraag c?
         
6. examenvraagstuk HAVO Wiskunde A, 1995.
         
  In de archeologie probeert men aan de hand van opgravingen na te gaan hoe vroegere samenlevingsvormen er uit gezien hebben en hoe ze veranderd zijn.
Samenlevingsvormen verschillen van elkaar als bijvoorbeeld economische of godsdienstige kenmerken anders zijn: denk daarbij bijvoorbeeld aan goud als ruilmiddel  in tegenstelling tot het gebruik van papiergeld, veelgodendom tegenover aanbidding van een enkele god.
  De ene samenlevingsvorm kan overgaan in een andere. Murdock heeft voor een aantal samenlevingsvormen onderzoek gedaan naar hun mogelijke opvolgers. In de figuur 1 hiernaast heeft hij zijn resultaten samengevat. Je kunt daar bijvoorbeeld aflezen dat de samenlevingsvorm Matri-Hawaiian kan overgaan in één van de drie samenlevingsvormen: Bi-Eskimo, Patri-Eskimo en Normal-Hawaiian. Van deze drie heeft alleen Patri-Eskimo een mogelijke opvolger die in dit schema voorkomt, namelijk Normal-Eskimo.

Het schema van deze figuur is op te vatten als een matrix: een zwart blokje staat voor 1: er is directe opvolging mogelijk; een wit blokje staat voor 0: er is geen directe opvolging mogelijk.

We bekijken eerst een deel van deze figuur. Dit gedeelte geven we weer in de onderstaande matrix M; naast de matrix is de bijbehorende graaf getekend.
         
 

         
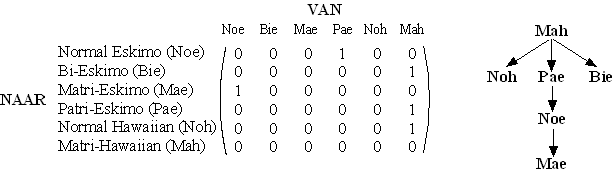  Als matrix M met zichzelf vermenigvuldigd wordt, ontstaat matrix M2.
         
  a. Schrijf matrix M2 op.
         
  Een samenlevingsvorm A wordt een niet-directe opvolger van samenlevingsvorm B genoemd als A wel in de keten van opvolgers van B zit, maar niet direct op B volgt.
Bijvoorbeeld:  B → ... → A  of    B → ... →  ... → A. Om enig inzicht te krijgen in de niet-directe opvolging van samenlevingsvormen kan men de matrices M2, M3 (= M • M • M). enzovoorts bekijken. De matrix M3 heeft nog slechts op één plaats een getal staan dat niet gelijk is aan 0.
         
  b. Leg uit op welke plaats in de matrix M3 dit getal staat en hoe groot dat getal is.
         
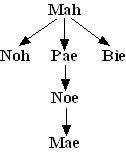
  We gaan terug naar de figuur 1. Figuur 1 is niet in één oogopslag te doorzien. De graaf die bij matrix M is gemaakt biedt een veel duidelijker overzicht van alle mogelijke overgangen tussen de diverse samenlevingsvormen die in M vermeld staan.
De graaf hiernaast is een deel van de complete graaf die bij figuur 1 hoort.

       
  c Breid deze graaf zo uit dat alle samenlevingsvormen en alle mogelijke overgangen die in figuur 1 genoemd worden in deze graaf komen te staan.
         
   
       

© h.hofstede (h.hofstede@hogeland.nl)