|
|
 |
|
Venn-Diagrammen. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
Dwars door Arnhem stroomt de Rijn.
Nou is het in Arnhem nogal belangrijk of je ten Noorden van de Rijn
woont of ten Zuiden. Ze spreken van `noorderlingen` en van
`zuiderlingen` en die twee bevolkingsgroepen trekken eigenlijk
nauwelijks met elkaar op. ´t Is nog nét geen ruzie....
Een wiskundeleraar aan een school midden in Arnhem heeft in zijn klas
leerlingen die noorderling zijn (N), en ook leerlingen die zuiderling
(Z) zijn. |
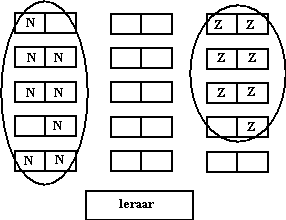
Ze zitten inderdaad per`soort` bij elkaar met
grote ruimte tussen beide groepen. Dat kun je op de plattegrond van de
klas hiernaast wel zien.
Maar dan komen er op een dag twee nieuwe leerlingen in de klas die een
tweeling zijn met gescheiden ouders. De vader woont in Noord, en de
moeder in Zuid en beide kinderen wonen af en toe bij vader en af en toe
bij moeder. Ze hebben daarom vriendjes in Noord én in Zuid.
Ze gaan daarom maar in de middelste rij zitten, want ze horen eigenlijk
bij Noord én bij Zuid. Ze willen ook niet kiezen eigenlijk. |
 |
| |
|
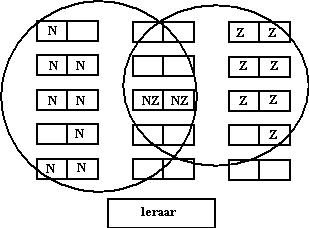
De wiskundeleraar bedenkt zich dat zijn
plattegrond dan eigenlijk moet worden als hiernaast.
Met twee van die cirkels door elkaar getekend klopt het helemaal: alle
leerlingen uit Zuid zitten nu in de ene cirkel en alle leerlingen uit
Noord in de andere. En de nieuwe leerlingen die bij beiden horen zitten
inderdaad in beide cirkels.
Hij leunt tevreden achterover....Hij vindt zichzelf nogal slim....
Als echte wiskundeleraar houdt hij van netheid en van orde.
|
 |
| |
|
En verdomd! Zijn systeem werkt geweldig!!!!
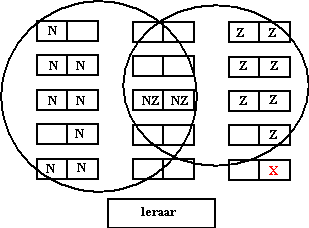
Later in het jaar komt er een leerling bij die zelfs helemaal niet in
Arnhem woont. Die zet hij dan gewoon aan een tafeltje buiten beide
cirkels!
Bijvoorbeeld op die plaats X hiernaast.
Zo heeft de leraar nu al 4 "gebieden " in zijn klas, namelijk
"Noord (N)" , "Zuid (Z)" , "NoordZuid (NZ) " en "Elders (X)
".
Je zou het schematisch zó kunnen tekenen (we stappen nu even af van het
klaslokaal en maken er als echte wiskundigen meer schematische
tekeningen van): |
 |
|
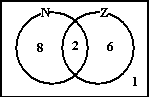 |
|
| |
|
| De hele rechthoek stelt het
klaslokaal voor, de beide cirkels de leerlingen uit Noord en uit Zuid.
Let erop dat de aantallen nu precies kloppen. Deze schematische manier
van aantallen weergeven heet een Venn-diagram. (genoemd naar de Engelse
wiskundige John Venn) |
| |
|
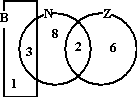
| Stel dat deze wiskundeleraar er later nog
drie kinderen bij krijgt waarvan de ouders gescheiden zijn, waarbij de
ene ouder buiten Arnhem woont en de andere in Noord. Dan kan hij zijn
Venn-diagram eenvoudig aanpassen zoals hiernaast is gebeurd (B = buiten
Arnhem) |
 |
| |
|
Of misschien is het mooier van die rechthoek
ook een cirkel te maken, en die ook met beide andere gebieden te
laten overlappen, zoals hiernaast is gebeurd. Dan kan hij ook leerlingen
kwijt waarvan de ene ouder buiten Arnhem woont en de andere in Zuid.
(het gebied waar alle drie de cirkels elkaar snijden is een beetje
apart: een leerling die deels buiten Arnhem, deels in Noord én deels in
Zuid woont???? Drie ouders??? Zal meestal leeg blijven...) |
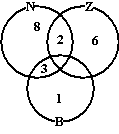 |
| |
|
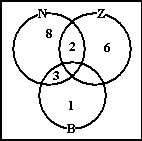
| En met nog weer een blok eromheen zouden in
de ruimte buiten alle cirkels maar wel binnen het blok de kinderen staan
die helemaal niet op deze school zitten (buiten het klaslokaal van de
drie cirkels).....Daarvan vinden we het dan niet interessant waar ze
wonen natuurlijk. |
 |
| |
|
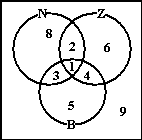
Deze manier van aantallen weergeven is erg
efficiënt.
Kijk maar eens naar het Venndiagram hiernaast en beantwoord zo snel
mogelijk de volgende vragen:
• Van hoeveel leerlingen woont één ouder buiten Arnhem en de
ander in Zuid?
• Van hoeveel leerlingen woont minstens één ouder in Noord?
• Van hoeveel leerlingen wonen beide ouders buiten Arnhem? |
 |
| |
|
Je ziet dat je met zo'n
Venn-diagram zulk soort vragen supersnel kunt beantwoorden, hoop ik.
Denk er in de volgende vragen goed om dat elke cirkel staat voor een
"eigenschap": |
| |
|
|
Probeer gewoon slimme
cirkels te tekenen!! |
|
| |
|
Heb je de smaak te pakken
gekregen van deze Venn-diagrammen?
Ben je een liefhebber geworden?
Dan kun je in de les hiernaast je nog verder verdiepen. |
|
|
| |
|
|
OPGAVEN |
| |
|
| 1. |
In een klas van 28 leerlingen zijn op het proefwerk Engels 6 onvoldoendes
gevallen.
Op het proefwerk Wiskunde zijn 11 onvoldoendes gevallen.
Er waren 4 leerlingen die op beide proefwerken een onvoldoende hadden.Hoeveel leerlingen hadden voor beide proefwerken een voldoende?
|
| |
|
|
|
| |
|
|
|
| 2. |
Een verkeerscontrole bestaat onder andere uit een bandencontrole en
controle van de verlichting. Er werden 95 auto's gecontroleerd. Bij de
bandencontrole vielen 18 auto's door de mand. De verlichting bleek van 24 auto's
niet in orde. Er waren 10 auto's bij waarvan zowel banden als verlichting
onvoldoende waren. Bij hoeveel auto's werden geen gebreken aan banden of verlichting
geconstateerd?
|
| |
|
|
|
| |
|
|
|
| 3. |
Van de bevolking van Bloemendaal
blijkt uit een enquête dat 52% wil dat de gemeente meer
fietspaden aanlegt. 32% wil graag meer wandelpaden.
Maar ook een groot aantal mensen vindt het wel best zoals het nu
is: 26% vindt dat geen van beide soorten paden moet worden
uitgebreid.
Er deden 550 mensen aan de enquête mee.
Hoeveel mensen uit de enquête wilden meer fietspaden, maar
vonden het aantal wandelpaden genoeg? |
| |
|
|
|
| |
|
|
|
| 4. |
In bejaardentehuis Rustoord
verschijnen de laatste tijd steeds meer rollators en
gehoorapparaten.
Bij een laatste telling onder de 870 bejaarden van het tehuis
bleek 70% een gehoorapparaat te hebben. Er waren 298 mensen met
een rollator.
540 bejaarden hadden wel een gehoorapparaat maar geen rollator.
Hoeveel bejaarden waren er nog zonder rollator en zonder
gehoorapparaat? |
| |
|
|
|
| |
|
|
|
| 5. |
Van 190 personen hebben
er 120 een facebook-account, 100 hebben een Hyves-pagina en 70
zitten er bij LinkedIn. Er is niemand die geen van deze drie
heeft.
Er zijn er 48 die zowel bij Facebook als bij Hyves zitten,
35 die zowel bij Hyves als bij LinkedIn zitten, en 40
hebben zowel Facebook als LinkedIn.
Hoeveel van deze mensen hebben alleen Hyves, en geen van de
andere beiden?
|
| |
|
|
|
| |
|
|
|
| 6. |
86 op de 1000 mensen heeft last van
slapeloosheid.
90% van de mensen met last van slapeloosheid drinkt koffie.
77% van de mensen zonder slapeloosheid drinkt koffie.
Hoeveel procent van de koffiedrinkers heeft last van slapeloosheid?
|
| |
|
|
|
| |
|
|
|
| 7. |
Een
fietsclub telt 120 leden.
Ze hebben allemaal tenminste één fiets (ja dûh).
54 leden hebben een racefiets, 48 een mountainbike, en 38 een
ligfiets.
18 leden hebben zowel een mountainbike als een racefiets.
Geen van de leden heeft zowel een ligfiets als een mountainbike.
Hoeveel leden hebben alleen een racefiets? |
| |
|
|
|
| |
|
|
|
| 8. |
84% van de kinderen op school hebben
een kat of een hond.
20% van de kattenbezitters heeft ook een hond.
10% van de hondenbezitters heeft ook een kat.
Hoeveel procent van de schoolkinderen heeft een kat? |
| |
|
|
|
| |
|
|
|
| 9. |
Olympiadevraagstuk
Op een kantoor werken 18 personen: één enkele
spreekt Nederlands, Frans
en Engels; 3 spreken Frans en Engels; 13 personen spreken Nederlands en
5 onder hen ook Engels; 9 spreken Frans;
niemand spreekt uitsluitend Engels.
Hoeveel personen op dat
kantoor spreken uitsluitend Frans? |
| |
|
|
|
| |
|
|
|
| 10. |
Tegenwoordig blijkt 3% van de brugklassers dyscalculie te
hebben,
Verder is 9% dyslectisch.
2% blijkt dyscalculie te hebben én dyslectisch te zijn.
Hoeveel procent van de leerlingen is heeft van geen van beiden
last? |
| |
|
|
|
| |
|
|
|
| 11. |
Van de werknemers van een bedrijf
speelt iedereen voetbal of tennis.
1/7 van de voetbalspelers speelt ook
tennis
1/9 van de tennisspelers speelt ook
voetbal.
Hoeveel procent van de werknemers speelt tennis? |
| |
|
|
|
 |
|
| |
|
|
 |
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|