| |
 |
|
Een variabel punt. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
|
|
| Als je een vectorvoorstelling van
een lijn hebt, dan zie je daaraan direct dat een willekeurig punt van
die lijn maar van één getal afhangt. Dat getal is namelijk de enige
letter in zo'n vectorvoorstelling, en die heet meestal
λ. Als
λ bekend
is, is het punt dat erbij hoort ook bekend. Bij elk punt hoort precies
één
λ, en bij elke
λ
hoort precies één punt. |
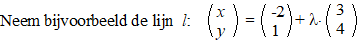 |
Dan heeft een willekeurig punt P
van die lijn de coördinaten P = (-2 + 3λ,
1 + 4λ).
Zie je wel? Zei ik toch? Alleen maar een
λ.... |
| |
|
|
|
|
Wat kun je d'r mee? |
| |
|
|
|
Ach, eigenlijk van alles.....
Hier volgt een kleine greep uit de talloze mogelijkheden...Volg de
voorbeelden maar, en je krijgt vanzelf een idee van "Hoe het werkt".
Eigenlijk doe je alle berekeningen met vectoren uit de vorige lessen nu
met een variabele (λ) erin.
1. snijpunten uitrekenen. |
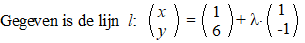 |
| En verder is er de cirkel
x2 + y2 = 25. Bereken de
snijpunten van de lijn met de cirkel. |
| |
|
|
|
Begin eerst met vast te stellen
dat een variabel punt van de lijn het punt (1 + λ, 6
- λ) is.
Dat punt moet dus óók op die cirkel liggen. Maar dat betekent dat je de
coördinaten van dat punt kunt invullen in de vergelijking van de cirkel.
Dat moet dan kloppen.
Dat geeft (1 +
λ)2 + (6 -
λ)2 = 25
⇒ 1 + 2λ +
λ2 + 36 - 12λ
+
λ2 = 25
⇒ 2λ2
-
10λ - 12 = 0 ⇒
λ2
- 5λ
+ 6 = 0
⇒ (λ
-
2)(λ
-
3) = 0 ⇒
λ
= 2 ∨ λ
= 3
Het variabele punt was (1 +
λ, 6 -
λ) en dat is dan nu geworden: (3, 4) en
(4, 3). |
| |
|
|
|
| 2. afstanden
uitrekenen. |
| |
|
|
|
| Voor de afstand d tussen
twee punten P(xP, yP) en Q(xQ,
yQ) geldt: |
| |
|
|
|
|
d =
√( (xP
- xQ)2 + (yP
- yQ)2 )
|
|
| |
|
|
|
Maak je niet al te druk; daar
staat eigenlijk gewoon Pythagoras.
Maar natuurlijk kan één van die punten (of zelfs beiden) best een
variabel punt zijn. Waarom niet? |
| |
|
|
|
| Voorbeeld: |
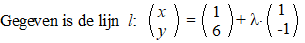 |
Welk punt van deze lijn heeft
afstand 3√2 tot het punt P(7,
6)?
Nou, een variabel punt van deze lijn is nog steeds (1 + λ, 6
- λ)
net als in het vorige voorbeeld.
De afstand van dit variabele punt tot P(7, 6) is dan gelijk aan (met de
d-formule hierboven) :
√((1 +
λ - 7)2 + (6
- λ
- 6)2 ) = √((λ
- 6)2 + (-λ)2) =
√(2λ2 -
12λ + 36) = 3√2
Kwadrateren: 2λ2 - 12λ
+ 36 = 18 ⇒ 2λ2
- 12λ + 18 = 0
⇒ λ2
- 6λ + 9 = 0 ⇒
(λ - 3)2 = 0
⇒
λ = 3
Dat geeft het punt (4, 3) |
| |
|
|
|
| 3. hoeken uitrekenen. |
| |
|
|
|
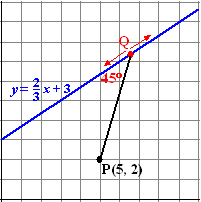
Voorbeeld.
P is het punt (5, 2)
Ergens op de lijn y = 2/3x
+ 3 ligt een punt Q zodat PQ een hoek van 45º maakt met de lijn (zie de
figuur).
Bereken de coördinaten van Q. |
 |
| |
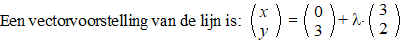 |
| een variabel punt Q
is dus (3λ, 3 + 2λ). |
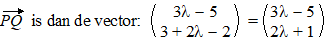 |
| De hoek tussen deze
vector en de richtingsvector van de lijn bereken je natuurlijk met die
inproductformule: |
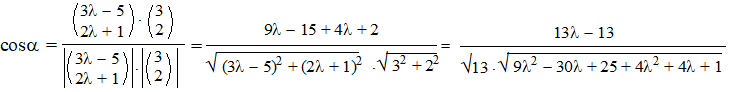 |
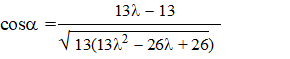 |
Dat moet gelijk zijn
aan cos 45º = 1/2√2.
Dus 1/2√2
• √(169l2
- 338l + 338) = 13λ
- 13.
Beide kanten kwadrateren: 1/2
• (169λ2 - 338λ
+ 338) = (13λ - 13)2 = 169λ2
- 338λ + 169.
Hergroeperen: 169λ2 - 338λ
= 0 ⇒ 169λ(λ
- 2) = 0 ⇒
λ
= 0 ∨
λ
= 2.
λ = 0 geeft het punt Q(0, 3) en
λ = 2 geeft het punt Q(6, 7). |
| |
|
|
|
| 4.
bewijzen. |
| |
|
|
|
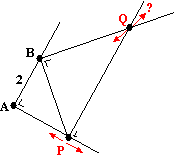
Zie de figuur
hiernaast.
A en B zijn vaste punten, met AB = 2.
Punt P beweegt over de loodlijn in A van AB.
BQ staat loodrecht op PB, en Q ligt op de loodlijn van AP in punt P.
Toon aan dat punt Q over een parabool beweegt. |
 |
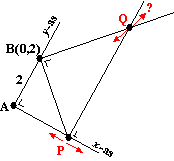
Leg eerst een
assenstelsel aan. Bijvoorbeeld zoals hiernaast met A = (0,0) en B
= (0,2). P loopt dan over de x-as.
P is het variabele punt (λ, 0) |
 |
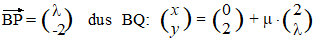 |
Q is het variabele
punt (2μ, 2 +
μλ)
Maar de x-coördinaat van Q is gelijk aan
λ (want Q ligt ook op de
loodlijn PQ) dus geldt 2μ =
λ
Dan is Q = (2μ, 2 +
μ • 2μ) = (2μ,
2 + 2μ2) |
Ga
m elimineren:
x = 2μ geeft
μ = 1/2x
dus dan is y = 2 + 2μ2
= 2 + 2(1/2x)2
= 2 + 1/2x2
Dat is inderdaad de vergelijking van een parabool. |
| |
|
|
|
|
OPGAVEN |
| |
|
|
| 1. |
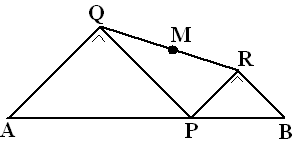
Op een lijnstuk AB met
lengte 8 wordt punt P gekozen.
Op AP en BP worden gelijkbenige rechthoekige driehoeken AQP en
PRB geconstrueerd met Q en R aan dezelfde kant van AB.
M is het midden van RQ.
Wat wordt de verzameling punten M als P lijnstuk AB
doorloopt? |
 |
| |
|
|
|
|
| 2. |
Gegeven is punt P(11, 5)
Welk punt van de lijn y = 2x + 3 heeft afstand 10
tot P? |
| |
|
|
|
|
| |
|
|
| 3. |
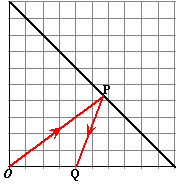
Vanaf de oorsprong O
trekken we een lijn naar een punt P dat ergens op de lijn
y = 10 - x ligt, en vervolgens gaan we in een
rechte lijn van P naar het punt Q(4, 0)
Voor welke P is de totale afgelegde afstand minimaal?
Geef de coördinaten in twee decimalen nauwkeurig. |
 |
| |
|
|
|
|
| |
|
| 4. |
P is het punt (1, 2) en Q is
het punt (8, 5), R is een punt van de y-as.
Wat is de maximale waarde voor hoek PRQ? Geef je antwoord
in graden en in twee decimalen nauwkeurig. |
| |
|
|
|
|
| |
|
|
|
|
| 5. |
Examenvraagstuk Wiskunde B,
2017-I |
| |
|
|
|
|
| |
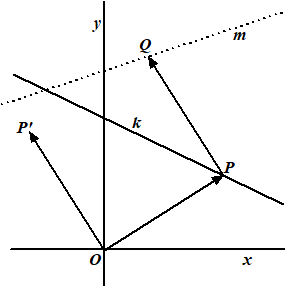
Gegeven is lijn k met vergelijking y
=
1/2x
+
3 . Op deze lijn ligt het punt P.
Vector OP wordt om de oorsprong over 90° linksom
gedraaid. Zo ontstaat vector OP'
Vector PQ heeft dezelfde richting en dezelfde lengte als
OP'. Zie de figuur. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
Wanneer het punt P over lijn k beweegt,
zal het punt Q over een lijn m bewegen. In de figuur is
m gestippeld weergegeven.
Stel een vergelijking van lijn m op. |
| |
|
|
|
|
| 6. |
Examenvraagstuk Wiskunde B,
2019-I |
| |
|
|
|
|
| |
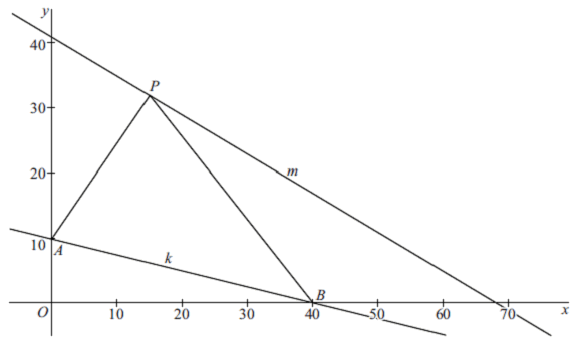
Lijn
k gaat door
de punten
A(0,10)
en
B(40,
0)
.
De baan van een
punt
P is gegeven
door de volgende bewegingsvergelijkingen:
x(t)= 18 + 5t en y(t)
= 30
- 3t
De baan van punt
P is de lijn
m. Zie de
figuur. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
Bij bijna elke positie van punt
P vormen de
punten
A,
B en
P een
driehoek
ABP. Er is
één uitzondering. |
| |
|
|
|
|
| |
a. |
Bereken de coördinaten van
P zodat
A,
B en
P niet de
hoekpunten van een driehoek vormen. |
| |
|
|
|
|
| |
b. |
Onderzoek op algebraïsche wijze
of er een positie van
P is, zó dat
driehoek
ABP een
rechte hoek heeft bij
P én driehoek
ABP een
gelijkbenige driehoek is. |
| |
|
|
|
|
| 7. |
Examenvraagstuk Wiskunde B,
2022-II |
| |
|
|
|
|
| |
Voor 0
≤ t ≤ 2π beweegt een punt P over
een cirkelvormige baan cP met middelpunt
O(0, 0) volgens de bewegingsvergelijkingen: |
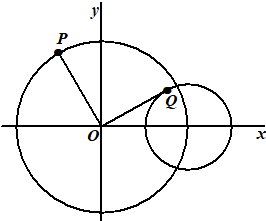 |
| |
|
|
| |
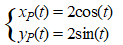 |
| |
|
|
| |
Voor 0
≤ t ≤ 2π beweegt tegelijkertijd een punt Q over
een cirkelvormige baan cQ volgens de
bewegingsvergelijkingen: |
| |
|
|
| |
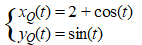 |
| |
|
|
|
|
| |
Hoek
POQ is afhankelijk van t. In de figuur zijn beide
cirkels cP en cQ
weergegeven. Ook zijn de lijnstukken OP en OQ
weergegeven voor een waarde van t waarvoor OP
en OQ loodrecht op elkaar staan. |
| |
|
|
|
|
| |
a. |
Bereken
exact de waarden van t waarvoor OP en OQ
loodrecht op elkaar staan |
| |
|
|
|
|
| |
De lijn
door P en Q snijdt de x-as in punt A.
De x-coördinaat van A is onafhankelijk van
t. |
| |
|
|
|
|
| |
b. |
Bewijs dit. |
| |
|
|
|
|
| |
Punt
M is het midden van lijnstuk PQ.
Op t = 0 beginnen P en Q vanaf de x-as
naar boven te bewegen. Punt M beweegt dan mee naar
boven. In de volgende figuren is voor drie waarden van t
de situatie weergegeven. |
| |
|
|
|
|
| |
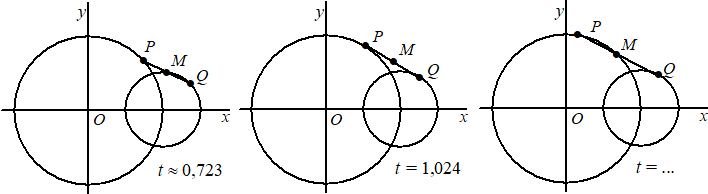 |
| |
|
|
|
|
| |
Voor
t ≈ 0,723 ligt punt M op cirkel cQ.
Zie de linkerfiguur. Na t ≈ 0,723 komt M in
het gebied buiten cQ te liggen. Zie de
middelste figuur. Op een zeker tijdstip ligt M op
cirkel cP. Zie de rechterfiguur.
Punt M ligt een percentage van de tijd waarin de
punten P en Q een volledige baan doorlopen
buiten cP en cQ. |
| |
|
|
|
|
| |
c. |
Bereken
dit percentage. Geef je eindantwoord als geheel getal. |
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|