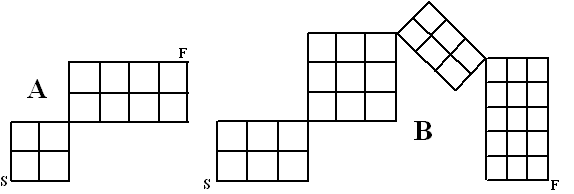© h.hofstede (h.hofstede@hogeland.nl)

       
1.

       
2.

       
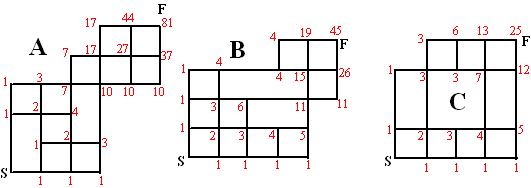
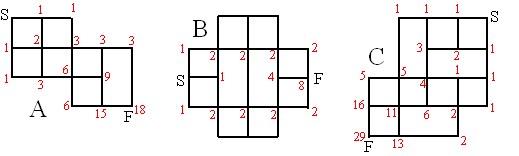
3. Kijk bij elk veld vanaf welke velden je er kunt komen. Je komt dus steeds van links, boven, of linksboven. Tel de routes van die velden op. Dat geeft:
       
 

       
  Dus dat zijn  63 en 106 en 186 manieren.
       
4.

       
  a. (4 nCr 2) • (6 nCr 4) = 90
       
  b. (5 nCr 2) • (6 nCr 3) • (5 nCr 2) • 8 nCr 3) = 112000
       
5. Voor elke route moet er 5 keer worden beslist  Rechts of Links.
A: 5L kan op 1 manier
B:  4L + 1R  kan op  5 nCr 4 = 5 manieren
C:  3L + 2R  kan op  5 nCr 3 = 10 manieren
D:  2L + 3R  kan op  5nCr 2 = 10 manieren
E:  1 L + 4R  kan op  5 nr 1 = 5 manieren
F:  5R kan op 1 manier.
       
6. Je moet zes stapjes nemen:  3 naar links en 3 naar rechts.
Dat kan op 6 nCr 3 =  20 manieren.
       
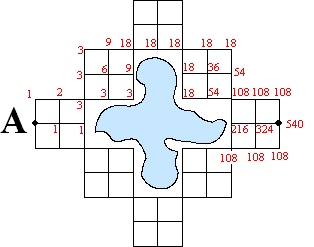
7. Zie hiernaast.

De onderkant is niet helemaal ingevuld maar is gelijk aan de bovenkant.

540 routes.
       
8. Een route ziet eruit als RRRAAABBB  (R = rechts, B = boven, A = achter)
Hoeveel zulke rijtjes letters zijn er?
(9 nCr 3) • (6 nCr 3) = 1680   (Zie de les over anagrammen.)
       
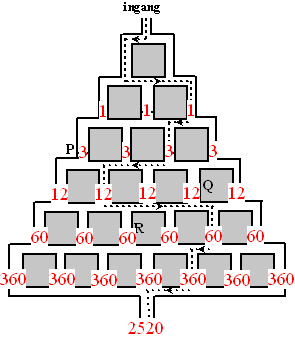
9. Zie hiernaast. Zet het aantal mogelijke routes bij de klapdeurtjes.
Dat geeft in totaal 2520 routes.

OF:
De rat kan achtereenvolgens kiezen uit  3-4-5-6 deurtjes
Dat kan op 3 • 4 • 5 • 6 = 360 manieren.
Er zijn 7 laatste deurtjes die naar de uitgang leiden, dus 7 • 360 = 2520 manieren.
       
10. a. Noem de teams A en B
Een mogelijkheid is AAAABB
Dat kan op  6 nCr 2 = 15 manieren.
       
  b. Van 0-0 naar 2-1  kan op  3 nCr 2 = 3 manieren
Van 2-1 naar 4-2  is een score van 2-1 en kan weer op 3 nCr 2 = 3 manieren
In totaal 3 • 3 = 9 manieren.
       
  c. Ga als A scoort een stap naar rechts en als B scoort een stap omhoog en elk scoreverloop geeft een route.
       

© h.hofstede (h.hofstede@hogeland.nl)