stochasten vermenigvuldigen


	© h.hofstede (h.hofstede@hogeland.nl)

Dingen met elkaar vermenigvuldigen.

Daarmee bedoel ik natuurlijk het volgende:
Je hebt een rij getallen {x₁, x₂, ..., x_n} met gemiddelde x_G en standaarddeviatie σ_x
Je hebt ook een rij getallen {y₁, y₂, ..., y_n} met gemiddelde y_G en standaarddeviatie σ_y

Als je die twee rijen getallen met elkaar vermenigvuldigt dan krijg je de rij {x₁y₁, x₂y₂, ..., x_ny_n}
Wat is het gemiddelde en wat is de standaarddeviatie van deze laatste rij getallen?

Het gemiddelde.

Het gemiddelde is vrij eenvoudig te vinden, als je je het volgende maar realiseert:

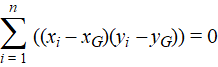Dat is zo als x en y onafhankelijk van elkaar zijn, en dat zagen we als in deze les.
Haakjes wegwerken:

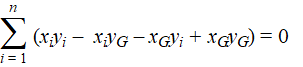splitsen in losse sommen:

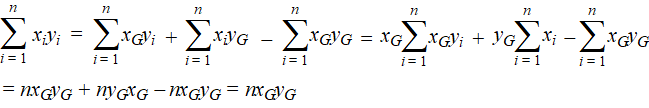Als je alles door n deelt vind je nu het gemiddelde van xy:

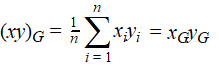Een aardig simpel resultaat:

(xy)_G = x_Gy_G

De standaarddeviatie.

Voor de standaarddeviatie gaan we de formule (x_i - x_G)(y_i- y_G) = x_iy_i - x_Gy_i - x_iy_G + x_Gy_G anders schrijven:
x_iy_i = (x_i - x_G)(y_i- y_G) + x_Gy_i + x_iy_G - x_Gy_G
x_iy_i = (x_i - x_G)(y_i- y_G) + x_Gy_i - x_Gy_G + x_iy_G - x_Gy_G + x_Gy_Gx_iy_i = (x_i - x_G)(y_i- y_G) + x_G(y_i - y_G) + y_G(x_i - x_G) + x_Gy_G

En nou maken we de aanname dat de standaarddeviatie veel kleiner is dan het gemiddelde.
Dat betekent dat die eerste term aan de rechterkant veel kleiner is dan beide anderen, want x_i - x_G en y_i - y_Gzijn de afstand tot het midden, en zijn dus veel kleiner dan x_G en y_G

Als je die eerste term verwaarloost, dan blijft over: x_iy_i = x_G(y_i - y_G) + y_G(x_i - x_G) + x_Gy_GDat betekent dat x_iy_i - x_Gy_G = x_G(y_i - y_G) + y_G(x_i - x_G)
Zet nu overal een somteken voor en ook nog ¹/_n en dan heb je de variantie σ² gevonden:

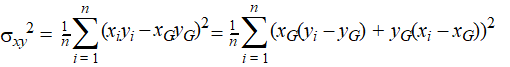Als x en y onafhankelijk zijn dan is dat middelste stuk weer nul (volgens dezelfde redenering die we ook al bij het berekenen van het gemiddelde bovenaan deze les gebruikten).
Dan blijft over:

Dit alles onder twee voorwaarden:
• x en y zijn onafhankelijk van elkaar
• de standaarddeviaties van x en y zijn veel kleiner dan hun gemiddelden.

Rekenvoorbeeldje:

Neem voor x de serie getallen (40, 42, 41) en voor y de serie getallen (92, 92, 98)
Dan is xy de serie getallen (3680, 3864, 4018)
invoeren in de GR geeft gemiddelde 3854 en standaarddeviatie is 138

x apart invoeren geeft gemiddelde 41 en standaarddeviatie 0,82
y apart invoeren geeft gemiddelde 94 en standaarddeviatie 2,83

onze formules voorspellen:
gemiddelde x_Gy_G = 31 • 94 = 3854 standaarddeviatie σ² = (41)² • 2,83²+ (94)² • 0,82² = 19404 dus σ = 139

Zoals je ziet klopt dat gemiddelde precies (moet ook want daar zat geen benadering in) en klopt die standaarddeviatie redelijk goed. Wijkt een beetje af natuurlijk vanwege beide rode voorwaarden hierboven. Met zo weinig getallen zal vooral aan de eerste voorwaarde meestal niet voldaan worden....