© h.hofstede (h.hofstede@hogeland.nl)

Sperner's Lemma
       
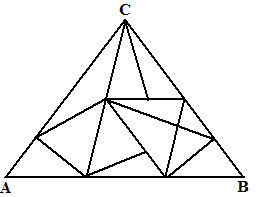
Verdeel een driehoek met hoekpunten A, B en C in allemaal willekeurige kleinere driehoeken, bijvoorbeeld zoals hiernaast.

Geef vervolgens alle hoekpunten van kleinere driehoeken ook een naam A, B of C.
Als je dat zó doet dat alle hoekpunten op zijde AB de namen A of B hebben (en die op zijde BC de namen B of C en die op zijde AC de namen A en C)  dan noemen we die naamgeving "correct".

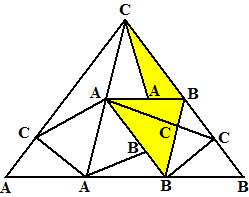
Hiernaast zie je een correcte naamgeving van driehoek ABC.
Daarin zijn een heleboel driehoeken te zien.
De driehoeken daarvan die alle drie de letters A, B en C als hoekpunten hebben noemen we "veelzijdig".

Ik heb in de figuur alle veelzijdige driehoeken geel gekleurd.

Je ziet dat het er drie zijn.
Dat is een oneven aantal....

Sperner's  Lemma zegt dat er altijd een oneven aantal veelzijdige driehoeken zijn (hij noemde ze trouwens "distinguished" in plaats van veelzijdig).

       

Elke correcte naamgeving van een onderverdeling van een driehoek  in kleinere driehoeken
geeft een oneven aantal veelzijdige driehoeken.
       
Bewijs.
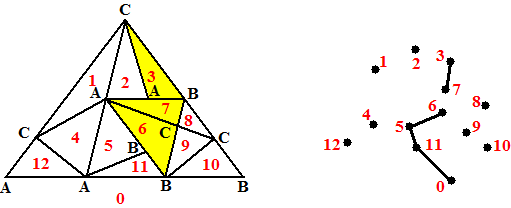
  Geef elke driehoek een nummer, en geef het buitengebied van driehoek ABC nummer 0.
Maak dan als volgt een graaf:
De knooppunten zijn de driehoeken.
Er is een verbindingslijn als twee driehoeken een zijde genaamd AB gemeenschappelijk hebben.

In ons voorbeeld zou dat het volgende opleveren:
       
 

       
  Dan heeft knooppunt 0 altijd een oneven graad.
Dat is makkelijk in te zien.

Begin met lijnstuk AB in een verder nog lege driehoek, dan is het aantal driehoeken dat via AB met gebied 0 is verbonden gelijk aan 1 (namelijk ABC zelf).
Ga nu op AB nieuwe punten A en B kiezen.
•  Elke keer als je een nieuw punt tussen een A en een B in kiest blijft het aantal lijnstukken dat via AB met gebied 0 is verbonden gelijk (dat nieuwe punt A/B vervangt gewoon de eerdere A/B)
•  Elke keer als je een nieuw punt tussen AA of tussen BB in kiest neemt het aantal lijnstukken dat via AB met gebied 0 is verbonden toe met 2.
Dus dat aantal blijft oneven.

Maar de vorige les bewezen we de stelling dat het aantal knooppunten van een graaf met oneven graad altijd even is.
Omdat knooppunt 0 oneven graad heeft, blijven er dus voor alle andere knooppunten (de driehoeken) een oneven aantal met een oneven graad over.

Maar geen enkel knooppunt kan graad 3 hebben!  Simpelweg omdat een driehoek nou eenmaal niet 3 zijden AB kan hebben.
Dus er zijn een oneven aantal knooppunten met graad 1  (in ons voorbeeld 3, 7 en 6)

De knooppunten met graad 1 zijn veelzijdig!
Ze moeten immers precies één zijde AB hebben, dus dat derde hoekpunt moet wel C zijn.
Daarmee is de stelling bewezen.

(hiernaast staat voor de liefhebber nog een alternatief bewijs, zonder de directe grafeneigenschap)
■    
       
Gevolg:  Brouwer Fixed Point Theorem
       
Uit Sperner's Lemma hierboven volgt:  
       

"Er is altijd minstens één veelzijdige driehoek"
       
Die eigenschap gaan we gebruiken om Brouwer-Fixed-Point-Theorem te bewijzen.
Dat luidt als volgt:
   

Bij elk continue functie f  die een gebied op zichzelf afbeeldt
is er een punt P  te vinden waarvoor geldt  f(P) = P
   
Simpeler gezegd:  "Er is altijd een punt dat op zichzelf terechtkomt".
Om eerlijk te zijn: er zijn nog wel een paar voorwaarden waaraan dat "gebied"  moet voldoen. Het moet bijvoorbeeld eindig zijn en convex (geen "gaten") en gesloten.  Kijk maar waarom het dan niet werkt:

•  eindig:  neem de functie  f(x) = x + 1
•  gesloten:  neem de functie  f(x) =  0,5x + 0,5  op het open interval  〈-1, 1〉
•  convex:  neem de punten op de omtrek van de eenheidscirkel en een functie die elk punt 20ş draait om de oorsprong.

Over naar het bewijs.......
   
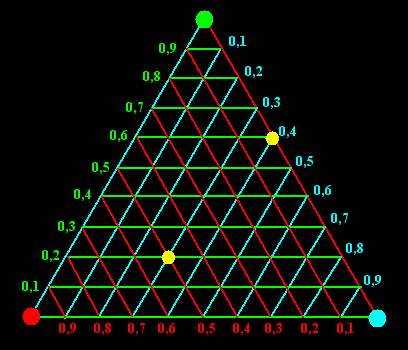
Eerst gaan we een coördinatenstelsel in de driehoek aanleggen. Dat doen we door "Driehoekscoördinaten" te nemen. Hiernaast staat hoe het werkt. Elk punt wordt gegeven door 3 coördinaten (x1, x2, x3) die samen 1 zijn. Welke je waar moet aflezen kun je aan de kleuren in de figuur hiernaast zien.
Als we de volgorde rood-blauw-groen nemen heeft het gele punt binnen de driehoek coördinaten (0.5 , 0.3 , 0.2)  en het gele punt op de rand  is het punt (0, 0.4 , 0.6). (De coördinaten stellen eigenlijk de gewichten voor die je op de hoekpunten zou moeten zetten om het zwaartepunt in het betreffende punt te krijgen, en worden ook wel "barycentrische" coördinaten genoemd)

Stel nu dat we een continue functie hebben die elk punt (x1, x2, x3) laat overgaan in een punt (x1', x2', x3').
Dan verdelen we de driehoek in allemaal hele kleine driehoekjes (zoals bij Sperner's Lemma) en gaan hem kleuren. Dat doen we volgens de volgende kleurregel:
       

Zoek de eerste coördinaat die bij het beeld kleiner is dan bij het origineel en geef het punt de kleur van die coördinaat
       
Als bijvoorbeeld punt (0.2 , 0.4 , 0.4) wordt afgebeeld op  (0.5 , 0.3 , 0.2) dan wordt het punt BLAUW omdat de tweede coördinaat de eerste is die kleiner is.
Dat lukt altijd; de coördinaten kunnen niet alle drie groter zijn omdat ze som 1 hebben. Als ze alle drie precies gelijk zijn hebben we meteen Brouwers Fixed Point bewezen.
Wat gebeurt er met punten op bijvoorbeeld de onderste rood-blauwe zijde? Die hebben coördinaten (x1 , x2, 0) en krijgen nieuwe coördinaten (x1', x2', x3'). Dan moet één van de eerste twee coördinaten van het beeld wel kleiner zijn dan die van het origineel. Allebei groter kan niet, wan x1 + x2 = 1, en als eentje groter is moet de ander wel kleiner zijn).  Kortom een punt op zijde rood-blauw wordt rood of blauw. Hetzelfde geldt voor de andere zijden, ga dat zelf maar na.
Conclusie: de kleuring van de punten is dezelfde als die bij Sperners Lemma.  Dus weten we dat er altijd een driehoek zal zijn met alle drie de kleuren (een "veelzijdige" driehoek).

Maak nu een verdeling in driehoeken en zoek de driehoek met alle kleuren.
Doe dat nogmaals met die veelzijdige driehoek: dus verdeel die weer in kleinere driehoeken.
Dan wéér kleinere driehoeken en ga zo alsmaar door (maak de driehoekenverdeling zo klein als je maar wilt). 

Elke keer zal er een driehoek zijn met alle kleuren (misschien wel meerderen). Die kan in het begin wel steeds op een andere plaats zitten, maar als de stapjes klein genoeg worden zul je uiteindelijk ergens een klein driehoekje krijgen dat "naar een punt P toegaat" (dat zal zo zijn als de driehoekjes klein genoeg zijn om de schommelingen in f  niet meer te"zien", want die schommelingen zijn eindig groot omdat f continu is).
Maar steeds zal blijven gelden  x1' ≤  x1 en x2' ≤  x2 en x3' ≤  x3. 
Omdat de som van de coördinaten 1 is, en de coördinaten (haast) niet meer veranderen, moet uiteindelijk gelden  x1' ≈ x1 en x2' ≈ x2 en x3' ≈ x3. Waarbij "≈" betekent "zo nauwkeurig als je maar wilt".
Dus is het punt P een  "fixed point" waarvoor geldt  f (P) = P.

Het is het punt op de kaart dat precies boven zichzelf terechtkomt!
       
En heel direct kun je inzien dat er zo'n fixed-point moet zijn als de kaart nadat er functie f op is toegepast gelijkvormig is met de originele. Hiernaast staat in het bovenste plaatje zo'n geval getekend.

Nu kunnen we het beeld als nieuw origineel kiezen en precies dezelfde functie weer toepassen. Dat geeft een tweede beeld.
Als we zo alsmaar doorgaan krijg je een serie beelden die naar een punt convergeren.

Dat is ons gezochte fixed-point!

 

Trouwens wist je....?
Dat je de haren op een kokosnoot niet zó kunt kammen dat er geen kruin is!

       
En waarom staat deze flauwekul hier nou zomaar?
Nou, 't is gewoon een toepassing van het fixed-point-theorem!
Beschouw het begin van de haren als x en het punt waar de haren eindigen als f(x). 
De kruin is het punt waar f(x) = x

Trouwens wist je.....?
  • Als je in een kop koffie roert is er na afloop minstens één koffiedeeltje dat zich op precies dezelfde plaats als in het begin bevindt....
  • Op het aardoppervlak is er altijd een punt waar het volledig windstil is.
  • Maak een kopie van een kaart, verfrommel die tot een prop en gooi die prop op de oorspronkelijke kaart. Dan ligt er altijd een punt van de prop precies boven zijn origineel!
       

© h.hofstede (h.hofstede@hogeland.nl)