© h.hofstede (h.hofstede@hogeland.nl)

 
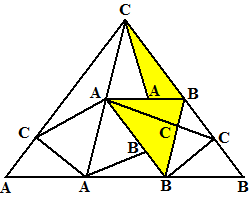
Laten we alle driehoeken in de figuur langslopen en tellen hoeveel AB-zijden we tegenkomen.
Noem dan:
  X = aantal AB-zijden van driehoeken die ABB of AAB zijn.
Y = aantal AB-zijden ten gevolge van ABC-driehoeken (veelzijdigen).
T = totaal aantal AB zijden.
     
Dan is T = X + Y want andere driehoeken leveren geen AB-zijden.

Laten we eerst T bepalen.

Er zijn twee soorten AB-zijden, namelijk zijden binnen in de driehoek, en zijden die een deel van de omtrek zijn. Van de eerste soort zullen we een even aantal vinden, omdat we elke zijde dubbel meetellen (hoort bij twee driehoeken).
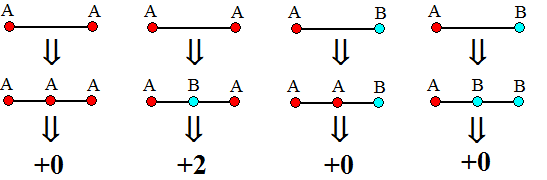
De tweede soort vinden we alleen op de oorspronkelijke AB-kant van de grote driehoek. Als we daarop vanaf het begin punten gaan toevoegen, dan zien we dat er vier mogelijkheden zijn:
       

       
A komt tussen twee A's, een B komt tussen twee A's, enz.
In de figuur hierboven zien we dat bij elk van die vier mogelijkheden het totaal aantal AB-zijden gelijk blijft of twee groter wordt. Omdat we oorspronkelijk begonnen met één AB-zijde, zal het aantal AB-zijden op de omtrek een oneven aantal zijn.

T is dus de som van een even aantal (binnenin) plus een oneven aantal (op de zijde) en zal dus oneven zijn.

Omdat elke driehoek van soort X twéé AB-zijden bijdraagt zal getal X een even getal zijn.
Omdat T = X + Y met T oneven en X even, zal Y dus een oneven aantal moeten zijn.
Dus de ABC-driehoeken leveren een oneven aantal AB-zijden.
Dus er is een oneven aantal veelzijdige driehoeken.
       
■      
       

© h.hofstede (h.hofstede@hogeland.nl)