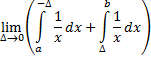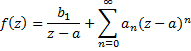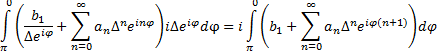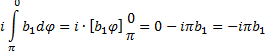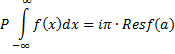singulariteiten op de integratieroute


	© h.hofstede (h.hofstede@hogeland.nl)

Singulariteiten op de integratieroute.

Neem de volgende, erg simpele, integraal:

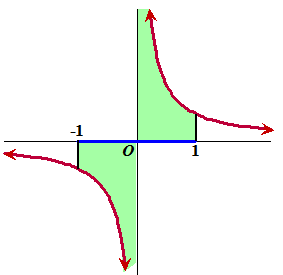
Daarbij loopt die integraal langs de reële as.
Waarschijnlijk zeg je nu iets als: "de primitieve van ¹/_x is ln|x| dus daar komt uit ln|b| - ln|a|"

En dan zou ik je helemaal gelijk moeten geven, ware het niet dat voor x = 0 die ¹/_x helemaal niet bestaat! Als a < 0 en b > 0 dan passeer je op je integratieroute een asymptoot!

Neem bijvoorbeeld de integraal in de figuur hiernaast met a = -1 en b = 1 (de blauwe route) Dan zou daar natuurlijk nul uit moeten komen. Dat zie je in één oogopslag, want die figuur is symmetrisch in de oorsprong, er zit evenveel groen oppervlak onder de x-as als boven de x-as.
Maar we vinden ln(1) - ln(-1) = 0 - ln(e^iπ) = -iπ

Dat klopt dus niet!

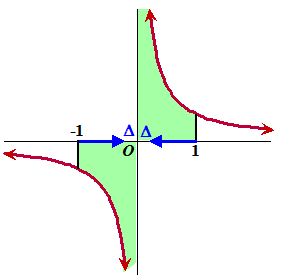
Je snapt intussen hopelijk al wel dat dat komt omdat in het complexe vlak bij z = 0 een singulier punt zit en dat ligt precies op onze integratieroute (de reële as). De oplossing om dit probleem te omzeilen is letterlijk dit probleem te omzeilen:

Knip gewoon het vervelende stukje weg!

Dan bereken je de integraal tot vlak vóór dat stukje, en vanaf vlak ná dat stukje:

Dat geeft:

Omdat a < 0 en b > 0 kun je dat ook zó schrijven:

En nu komt er voor a = -1 en b = 1 tenminste "gewoon" nul uit, zoals het hoort.
De waarde die we op deze manier vinden (dat simpele wegknippen van een stukje en dan dat stukje naar nul te laten gaan) heet de hoofdwaarde van de integraal, en die wordt meestal aangegeven door er een P voor te zetten (van Principal Value).

't Is trouwens wel een gedoe met al die limieten en zo, vind je niet? En ik vraag me ook af of dat zomaar met elke functie gaat lukken.....

Gelukkig is er een véééééééééél mooiere manier om zo'n singulier punt te omzeilen, vooral als je integralen langs de hele reële as neemt (dus van min-oneindig naar plus-oneindig) die je sluit via een grote halve cirkel, en die mooiere manier is: NOG letterlijker omzeilen!

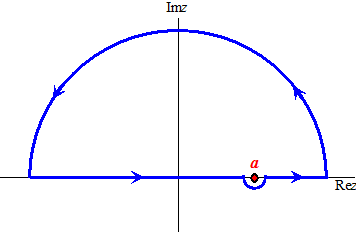
Kijk naar de integratieroute hiernaast in het complexe vlak.
Daar is de oorsprong gewoon vermeden door er "in een boogje omheen te zeilen".
De totale kringintegraal langs de hele blauwe integratieroute is nu nul, want de singulariteit is vermeden (neem even aan dat er niet nog meer andere singulariteiten binnen de route zijn).

Als we aannemen dat de integraal langs de grote halve cirkel ook nul is (f(z) gaat sneller dan ¹/_z naar nul) dan betekent dat, dat de hoofdwaarde van de integraal langs de reële as plus de integraal langs dat mini-halve-cirkeltje samen ook nul moeten zijn.

Op dat cirkeltje geldt z = a + Δe^iφ (Δ is de straal en die laten we naar nul gaan voor de hoofdwaarde). Daarbij loopt φ van π naar 0 want we gaan van links naar rechts.

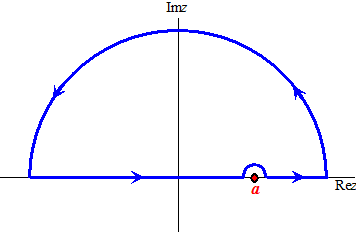Maar nou komt het: als de functie f een beetje normaal is, met een eerste orde singulariteit in z = a, dan kun je er de volgende reeksontwikkeling voor schrijven (een Laurentreeks, weet je nog?):

Voor de integraal langs dat mini-halve-cirkeltje geeft dat:

Dat hele stuk onder dat somteken gaat naar nul als Δ naar nul gaat (want die complexe e-macht is een eindig getal op de eenheidscirkel weet je nog?) Dus dan blijft over:

De integraal over de reële as is dan gelijk aan het tegengestelde hiervan, dus aan iπb₁

Grappig toch? Dat is precies de helft van het residu dat je zou krijgen als de singulariteit binnen de route zou liggen. En omdat dit een vrij algemene afleiding was, geldt dat eigenlijk altijd:

"eerste-orde singulariteiten op de routen tellen voor de helft mee"

Of, iets netter geformuleerd (P staat voor de hoofdwaarde):

We hadden natuurlijk net zo goed dat singuliere punt z = a kunnen omzeilen met een cirkeltje er onderlangs, zoals hiernaast.

En kijk hoe mooi het allemaal weer klopt: de integraal langs dat mini-halve-cirkeltje is nu iπ • Resf(a), want het draait de andere kant rond. Dus dat zou voor de hoofdwaarde -iπ • Resf(a) geven.

Maar nu zit er wél een singulier punt binnen de route, dus geeft een extra 2πi • Resf(a) zodat er gelukkig toch weer dezelfde waarde iπf(a) uitkomt voor de hoofdwaarde.