| |
 |
|
De simplex-methode. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
Misschien is het handig als je de
les over de randwandelingen eerst leest.....
Deze les gaan we dat randwandelen automatiseren.
Neem het volgende voorbeeld: |
| |
|
|
|
|
| |
|
Voor een feestavond
op school gaat de feestcommissie zelf cocktails maken. Om het
eenvoudig te houden gaan ze twee soorten cocktails maken uit de
basisdranken wodka en sinaasappelsap en champagne.
Dit zijn de twee cocktails: |
| |
|
|
|
|
| |
|
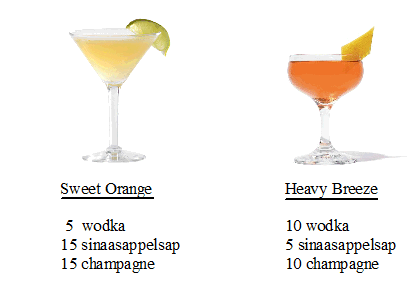 |
| |
|
|
|
|
| |
|
De hoeveelheden zijn
in cl.
Men heeft een hoeveelheid van 11 liter wodka en 12 liter
sinaasappelsap en 15 liter champagne in voorraad.
Hoeveel cocktails kan men maximaal maken? |
| |
|
|
|
|
| |
|
De oplossing is
eenvoudig:
Stel dat we S (sweet orange) en H (heavy breeze) cocktails gaan maken.
sinaasappelsap: 15S + 5H ≤ 1200
wodka: 5S + 10H ≤ 1100
champagne: 15S + 10H ≤ 1500
Doelstellingsfunctie: D = S + H maximaliseren
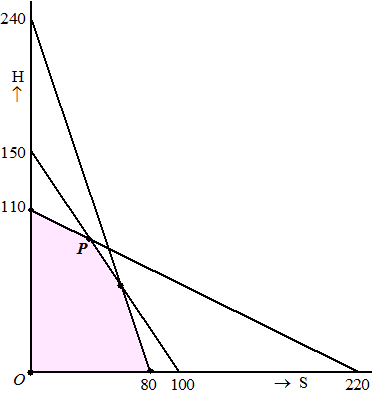
Dat geeft het toelaatbare gebied hiernaast, en een randwandeling levert
het maximale aantal van 130 cocktails in punt P (40 sweet orange
en 90 heavy breeze).
En daarmee is de randwandeling
ten einde. |
 |
| |
|
|
|
|
| |
|
 |
| |
|
|
|
|
|
Laten we dit proces gaan
automatiseren.... |
| |
|
|
|
|
Daarvoor introduceren
we eerst drie nieuwe variabelen, die aangeven hoeveel er NIET gebruikt
wordt. Stel:
• x = ongebruikte centiliters sinaasappelsap.
• y = ongebruikte centiliters wodka.
• z = ongebruikte centiliters champagne.
Deze variabelen heten spelingsvariabelen (engels:
slack variables).
Dat heeft het grote voordeel dat we bovenstaande ongelijkheden kunnen
veranderen in vergelijkingen, kijk maar: |
| |
|
|
|
|
| |
|
D
- S
- H = 0
15S + 5H + x = 1200
5S + 10H + y = 1100
15S + 10H + z = 1500
(met de aantekening dat alle variabelen, S, H, x, y, z
groter of gelijk aan nul moeten zijn) |
| |
|
|
|
|
| Het voordeel? |
| vergelijkingen kun je bij elkaar
optellen en van elkaar aftrekken |
|
| |
|
|
|
|
| We zoeken dus een
oplossing voor dit stelsel van 4 vergelijkingen. Omdat er meer
variabelen dan vergelijkingen zijn, zijn er natuurlijk oneindig veel
oplossingen, maar we zijn op zoek naar degene waarbij D maximaal is. |
| |
|
|
|
|
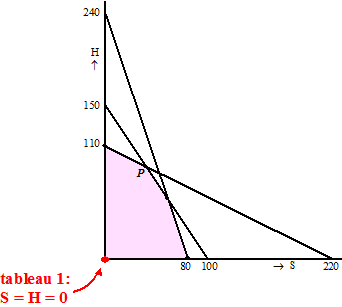
Stel nu dat we
beginnen met de situatie dat S = H = 0, en dus x = 1200,
y = 1100 en z = 1500
Al deze gegevens (vergelijkingen en beginwaarden) kunnen we als volgt in een zogenaamd
simplex-tableau
zetten (klinkt gewichtig, maar is niets anders dan een
overzichtelijke tabel): |
| |
|
|
|
|
| |
|
|
tableau 1 |
| basis |
D |
S |
H |
x |
y |
z |
rechts |
| D |
1 |
-1 |
-1 |
0 |
0 |
0 |
0 |
| x |
0 |
15 |
5 |
1 |
0 |
0 |
1200 |
| y |
0 |
5 |
10 |
0 |
1 |
0 |
1100 |
| z |
0 |
15 |
10 |
0 |
0 |
1 |
1500 |
|
| |
|
|
|
|
Ik hoop dat je ziet
dat daar gewoon die vier vergelijkingen nog een keer staan.
De variabelen in de eerste kolom heten de basisvariabelen,
en dat zijn de variabelen die in de gegeven situatie NIET nul zijn (dus
alle variabelen die niet in de eerste kolom staan zijn nul).
We begonnen in de situatie S = H = 0, en x =
1200, y = 1100, z = 1500. Dat komt overeen met hoekpunt
(0,0) in het toelaatbare gebied. Er zijn nog geen cocktails genmaakt; en dat kun je ook zien aan die rode nul van het simplex-tableau (rechts in de
D-vergelijking staat nul). |
| |
|
|
|
|
Oké, tot zover nog
niet veel speciaals gebeurd.
Maar nu gaan we die eigenschap van vergelijkingen (dat je ze kunt
combineren) op een handige manier gebruiken.
Kijk eens naar die bovenste vergelijking van tableau 1.
Daar staat D - S - H = 0
Die nul staat daar nogal sneu aan de rechterkant. Maar als we nou die S
of die H groter maken (basisvariabele gaan maken) dan wordt D
groter.
Als we S groter gaan maken, dan wandelen we als hert ware in ons
toelaatbare gebied van de oorsprong naar rechts.
Merk op dat, als je de waarden rechts in de S-kolom deelt door de
overeenkomstige getallen in de S-kolom zelf, je precies de punten op de
S-as in het toelaatbare gebied krijgt. |
 |
|
|
|
tableau 1 |
| basis |
D |
S |
H |
x |
y |
z |
rechts |
|
| D |
1 |
-1 |
-1 |
0 |
0 |
0 |
0 |
| x |
0 |
15 |
5 |
1 |
0 |
0 |
1200 |
1200/15
= 80 |
| y |
0 |
5 |
10 |
0 |
1 |
0 |
1100 |
1100/5
= 220 |
| z |
0 |
15 |
10 |
0 |
0 |
1 |
1500 |
1500/15
= 100 |
|
|
We kiezen nu de kleinste niet-negatieve van die drie (want we
mogen niet buiten het toelaatbare gebied komen), in dit geval de 80.
Het bijbehorende element uit de S-kolom is 15, en dat noemen we het
pivot-element (draai-element): |
| |
|
|
|
|
|
tableau 1 |
| basis |
D |
S |
H |
x |
y |
z |
rechts |
| D |
1 |
-1 |
-1 |
0 |
0 |
0 |
0 |
| x |
0 |
15 |
5 |
1 |
0 |
0 |
1200 |
| y |
0 |
5 |
10 |
0 |
1 |
0 |
1100 |
| z |
0 |
15 |
10 |
0 |
0 |
1 |
1500 |
|
| |
|
|
|
|
Door handig
vergelijkingen (rijen) te combineren gaan we nu proberen de S-kolom te
veranderen in 0 - 1 - 0 - 0
Deel de tweede rij door 15: |
| |
|
|
|
|
|
tableau 1 |
| basis |
D |
S |
H |
x |
y |
z |
rechts |
| D |
1 |
-1 |
-1 |
0 |
0 |
0 |
0 |
| x |
0 |
1 |
1/3 |
1/15 |
0 |
0 |
80 |
| y |
0 |
5 |
10 |
0 |
1 |
0 |
1100 |
| z |
0 |
15 |
10 |
0 |
0 |
1 |
1500 |
|
| |
|
|
|
|
| Tel deze tweede rij bij de bovenste op: |
| |
|
|
|
|
|
tableau 1 |
| basis |
D |
S |
H |
x |
y |
z |
rechts |
| D |
1 |
0 |
-2/3 |
1/15 |
0 |
0 |
80 |
| x |
0 |
1 |
1/3 |
1/15 |
0 |
0 |
80 |
| y |
0 |
5 |
10 |
0 |
1 |
0 |
1100 |
| z |
0 |
15 |
10 |
0 |
0 |
1 |
1500 |
|
| |
|
|
|
|
| Trek de tweede rij
5 keer van de derde af: |
| |
|
|
|
|
|
tableau 1 |
| basis |
D |
S |
H |
x |
y |
z |
rechts |
| D |
1 |
0 |
-2/3 |
1/15 |
0 |
0 |
80 |
| x |
0 |
1 |
1/3 |
1/15 |
0 |
0 |
80 |
| y |
0 |
0 |
25/3 |
-1/3 |
1 |
0 |
700 |
| z |
0 |
15 |
10 |
0 |
0 |
1 |
1500 |
|
| |
|
|
|
|
| Trek de tweede rij 15
keer van de onderste af: |
| |
|
|
|
|
|
tableau 1 |
| basis |
D |
S |
H |
x |
y |
z |
rechts |
| D |
1 |
0 |
-2/3 |
1/15 |
0 |
0 |
80 |
| x |
0 |
1 |
1/3 |
1/15 |
0 |
0 |
80 |
| y |
0 |
0 |
25/3 |
-1/3 |
1 |
0 |
700 |
| z |
0 |
0 |
5 |
-1 |
0 |
1 |
300 |
|
| |
|
|
|
|
Bedenk goed dat hier
nog steeds vier geldige vergelijkingen staan!!
De tweede rij (pivot-rij) geeft nu de vergelijking S +
1/3H +
1/15x
= 80
Maar omdat die S in de andere vergelijkingen niet meer voorkomt, kun je nu ook
S wel als basisvariabele schrijven.
We draaien als het ware S en x. Dat geeft dan tableau 2: |
| |
|
|
|
|
|
tableau 2 |
| basis |
D |
S |
H |
x |
y |
z |
rechts |
| D |
1 |
0 |
-2/3 |
1/15 |
0 |
0 |
80 |
| S |
0 |
1 |
1/3 |
1/15 |
0 |
0 |
80 |
| y |
0 |
0 |
25/3 |
-1/3 |
1 |
0 |
700 |
| z |
0 |
0 |
5 |
-1 |
0 |
1 |
300 |
|
| |
|
|
|
|
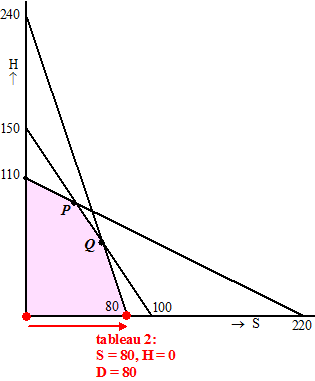
Merk alsjeblieft op
dat er door dat draaien niets aan de vergelijkingen is veranderd.
In het toelaatbare
gebied is er het volgende gebeurd: |
| |
|
|
|
|
|
 |
Welke kolom?
We kozen ervoor om
vanaf (0, 0) de variabele S te laten toenemen, dus zijn we opzij
gewandeld naar het volgende hoekpunt van het toelaatbare gebied. Zo zijn
we aangeland in punt (80,0) met D = 80 (rechtsboven in het simplex
tableau)
Als we in het begin voor de H-kolom in plaats van de S-kolom hadden
gekozen dan waren we omhoog gewandeld naar het punt (0, 110), dat
snap je vast wel.
Het is het handigst om de kolom te kiezen met het grootste negatieve
getal in de D-rij, want dan neemt D het snelst toe. In ons geval waren
beiden -1, dus maakte het niet uit.
Hoe verder?
In de bovenste rij zien we nu nog steeds een negatief getal -2/3
in de H-kolom staan. Dat betekent dat we D nog groter kunnen
maken. Deel de kolom rechts door de coëfficiënten uit de H-kolom en je
krijgt: |
| |
|
|
|
|
|
tableau 2 |
| basis |
D |
S |
H |
x |
y |
z |
rechts |
|
| D |
1 |
0 |
-2/3 |
1/15 |
0 |
0 |
80 |
| S |
0 |
1 |
1/3 |
1/15 |
0 |
0 |
80 |
80/1/3
= 240 |
| y |
0 |
0 |
25/3 |
-1/3 |
1 |
0 |
700 |
700/25/3
= 84 |
| z |
0 |
0 |
5 |
-1 |
0 |
1 |
300 |
300/5
= 60 |
|
| |
|
|
|
|
Het kleinste
niet-negatieve getal is 60, dus we kiezen het onderste element uit de
H-kolom als nieuw pivot-element.
Op dezelfde manier als hierboven gaan we nu de H-kolom veranderen in
0 - 0 - 0 - 1, zodat we H en z kunnen gaan draaien. Ik geef niet
alle tussenstappen, maar direct tableau 3, met H en z gedraaid: |
| |
|
|
|
|
|
tableau 3 |
| basis |
D |
S |
H |
x |
y |
z |
rechts |
| D |
1 |
0 |
0 |
- 1/15 |
0 |
2/15 |
120 |
| S |
0 |
1 |
0 |
2/15 |
0 |
-1/3 |
60 |
| y |
0 |
0 |
0 |
4/3 |
1 |
-5/3 |
200 |
| H |
0 |
0 |
1 |
-1/5 |
0 |
1/5 |
60 |
|
| |
|
|
|
|
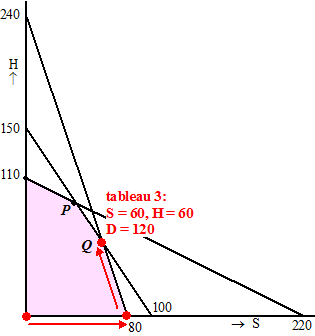
| Het nieuwe aantal
cocktails is 120. We zien aan de basisvariabelen van de eerste kolom dat
alleen de hoeveelheid y nog niet volledig is benut. Verder zien
we in de S-rij en H-rij dat de hoeveelheden S en H op het moment gelijk
zijn aan 60 en 60. |
| |
|
|
|
|
|
 |
| |
|
|
|
|
In het toelaatbare
gebied zijn we intussen gewandeld naar punt Q. Aan het feit dat we in Q
nog onder de grenslijn zitten die van 110 naar 220 loopt kun je trouwens
ook zien dat de y-hoeveelheid nog niet volledig is
benut.
Oké: de bovenste rij in tableau 3 laat zien dat
er nog een negatief getal bij x staat, dus D kan nog verder
vergroot worden. |
| |
|
|
|
|
|
tableau 3 |
| basis |
D |
S |
H |
x |
y |
z |
rechts |
|
| D |
1 |
0 |
0 |
- 1/15 |
0 |
2/15 |
120 |
| S |
0 |
1 |
0 |
2/15 |
0 |
-1/3 |
60 |
60/2/15
= 450 |
| y |
0 |
0 |
0 |
4/3 |
1 |
-5/3 |
200 |
200/4/3
= 150 |
|
H |
0 |
0 |
1 |
-1/5 |
0 |
1/5 |
60 |
60/-1/5 = -300 |
|
| |
|
|
|
|
Het pivot-element
wordt het derde element uit de x-kolom. Dat is het kleinste
niet-negatieve getal in die gele kolom.
Dat geeft het volgende tableau: |
| |
|
|
|
|
|
tableau 4 |
| basis |
D |
S |
H |
x |
y |
z |
rechts |
| D |
1 |
0 |
0 |
0 |
1/20 |
7/60 |
130 |
| S |
0 |
1 |
0 |
0 |
-1/10 |
1/6 |
40 |
| x |
0 |
0 |
0 |
1 |
3/4 |
-5/4 |
150 |
|
H |
0 |
0 |
1 |
0 |
3/20 |
-1/4 |
90 |
|
| |
|
|
|
|
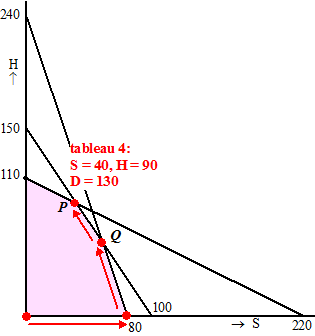
En nu zijn we klaar:
de bovenste rij bevat alleen nog maar positieve getallen, dus de waarde
van D kan niet verder vergroot worden. We zien uit dit laatste tableau
dat S = 40 en H = 90 en D = 130
Verder zien we dat van de x-hoeveelheid nog 150 cl
ongebruikt is, dus we houden 1,5 liter sinaasappelsap over.
15S + 5H = 15 • 40 + 5 • 90 = 1050 en dat is inderdaad 150 onder de
maximale 1500 cl sinaasappelsap.
Dat hoort allemaal bij punt P in het toelaatbare gebied. |
| |
|
|
|
|
|
 |
| |
|
|
|
|
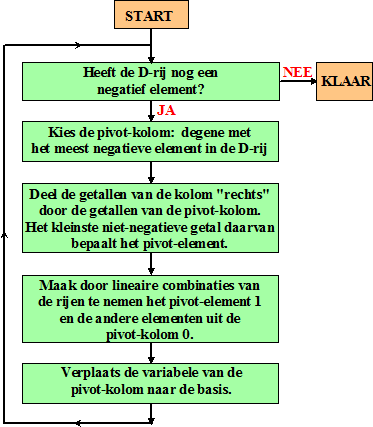
| Je kunt je
voorstellen dat dit typisch een werkje is voor een computerprogramma.
Hier volgt een stroomschema voor zo'n programma. Het vat meteen nog eens
samen wat we nou allemaal gedaan hebben. |
| |
|
|
|
|
|
 |
| |
|
|
|
|
| |
|
|
|
|
|
OPGAVEN |
| |
|
|
|
|
| 1. |
examenvraagstuk Wiskunde A, VWO, 1983. |
| |
|
|
|
|
| |
Een bedrijf maakt vier modellen
vliegtuigjes. Er worden twee uitvoeringen van een sportvliegtuig
gemaakt: de Super (S) en de Economy (E). Daarnaast worden er twee
versies gemaakt van een zweefvliegtuig: één echt zweefvliegtuig, de
Zwever (Z), en één met hulpmotor: de Motorzwever (M).
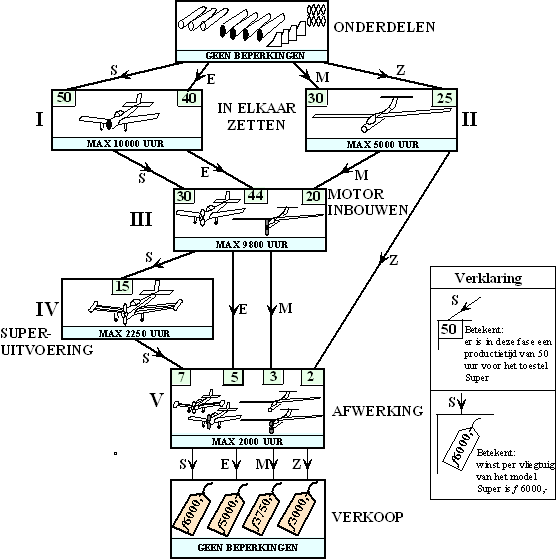
Het schema voor de productie staat in de figuur hieronder. Daaruit
blijkt onder anderen dat er naast het onderdelenmagazijn 5
productiehallen zijn die alle een maximale capaciteit hebben. Zo
heeft hal I een productiecapaciteit van 10000 uur.
De productietijden per model per hal staan ook in het schema
vermeld: bijvoorbeeld het in elkaar zetten van een 'Economy' 40 uur.
Tenslotte is ook de winst af te lezen uit het schema: bij de
'verkoop' blijkt de winst op een 'Super' f 6000,- te
bedragen. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
a. |
Stel een simplex-tableau op
voor de berekening van de maximale winst (Je hoeft de berekening
zelf niet uit te voeren). |
| |
|
|
|
|
| |
De berekening wordt door een
computer uitgevoerd. De laatste drie tableaus die de computer levert
zien er als volgt uit (1e kolom: Super, 2e
kolom: Economy, 3e kolom: Motorzwever, 4e
kolom: Zwever):
het simplex tableau ziet er
zó uit: |
| |
|
|
|
|
| |
0.00
0.00
0,00
1.00
0.00
0.00 |
1.00
0.00
0.00
0.00
0.00
0.00 |
0.00
0.00
1.00
0.00
0.00
0.00 |
0.00
25.00
0.00
0.00
2.00
3.00 |
0.03
1.65
-0.06
0.00
0.04
0.08 |
0.00
1.00
0.00
0.00
0.00
0.00 |
0.00
-1.50
0.05
0.00
-0.15
-0.19 |
-0.08
-1.50
0.05
0.07
-0.20
-0.17 |
0.00
0.00
0.00
0.00
1.00
0.00 |
62.50
3425.00
52.50
150.00
480.00
-1409.38 |
|
| |
De waarde van de
doelstellingsfunctie is 1409.38 |
| |
|
| |
het simplex tableau ziet er
zó uit: |
| |
0.00
0.00
0,00
1.00
0.00
0.00 |
1.00
0.00
0.00
0.00
0.00
0.00 |
0.00
0.00
1.00
0.00
0.00
0.00 |
0.00
1.00
0.00
0.00
0.00
0.00 |
0.03
0.07
-0.06
0.00
-0.09
-0.12 |
0.00
0.04
0.00
0.00
-0.08
-0.12 |
0.00
-0.06
0.05
0.00
-0.03
0.00 |
-0.08
-0.06
0.05
0.07
-0.08
0.00 |
0.00
0.00
0.00
0.00
1.00
0.00 |
62.50
137.00
52.50
150.00
206.00
-1820.38 |
|
| |
De waarde van de
doelstellingsfunctie is 1820.38 |
| |
|
|
|
|
| |
het simplex tableau ziet er
zó uit: |
| |
0.00
0.00
0,00
1.00
0.00
0.00 |
1.00
0.00
0.00
0.00
0.00
0.00 |
1.67
1.20
20.00
-1.33
1.60
-0.18 |
0.00
1.00
0.00
0.00
0.00
0.00 |
-0.07
0.00
-1.10
0.07
-0.18
-0.11 |
0.00
0.04
0.00
0.00
-0.08
-0.12 |
0.08
0.00
1.00
-0.07
0.05
-0.02 |
0.00
0.00
1.00
0.00
0.00
0.00 |
0.00
0.00
0.00
0.00
1.00
0.00 |
150.00
200.00
1050.00
80.00
290.00
-1830.00 |
|
| |
De waarde van de
doelstellingsfunctie is 1830.00
De optimale oplossing is nu gevonden.Aan de hand van deze
tableaus moeten de directeuren een beslissing nemen over de te
produceren aantallen toestellen.
De ene directeur (A) wil per se het productieschema uitvoeren dat
tot maximale winst leidt. De andere directeur (B) oppert de
mogelijkheid om te produceren volgens het middelste tableau: de
winst is wat minder, maar alle vier modellen worden
geproduceerd. |
| |
|
|
|
|
| |
a. |
Bepaal aan de hand van de
simplex-tableaus hoeveel stuks er van ieder model gemaakt moeten
worden, als directeur A zijn zin krijgt en hoeveel als directeur B
zijn zin krijgt. |
| |
|
|
|
|
| |
b. |
Bepaal bij ieder van de
onder b) genoemde productiemogelijkheden de gemiddelde winst
per vliegtuig. |
| |
|
|
|
|
|
| |
|
|
|
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |