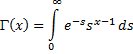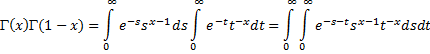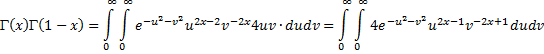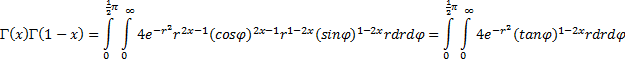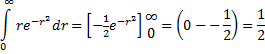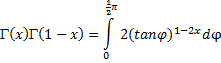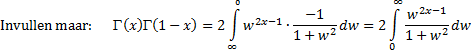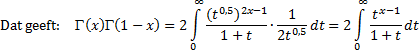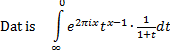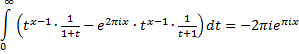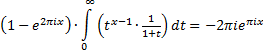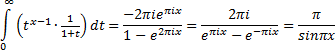|
|||||
| De reflectieformule met een contourintegraal. | |||||
| Het gaat er dus allemaal om, om deze formule te bewijzen: | |||||
|
|||||
| Nou, laten we dat dan maar gewoon rechtstreeks doen door de volgende definitie van de Γ-functie te gebruiken: | |||||
|
|
|||||
| Laten we die integralen voor Γ invullen en er een dubbelintegraal van maken: | |||||
|
|
|||||
| En nou gaan we een aantal keer
steeds op nieuwe variabelen overstappen, net zolang totdat we de
integralen kunnen uitrekenen. En natuurlijk ook omdat het gewoon
hartstikke leuk werk is. Het regent buiten, dus kan ik lekker een paar
uurtjes met wiskunde bezig. Hopen dat ik geen bezoek krijg.... eerste substitutie Noem u2 = s (dus ds = 2udu) en v2 = t (dus dt = 2vdv). |
|||||
|
|
|||||
| Daar staat eigenlijk dat we voor elk punt (u, v) van het vlakdeel (u, v ≥ 0) de waarde van die integrand moeten uitrekenen en dan al die waarden bij elkaar op moeten tellen. | |||||
|
tweede substitutie:
poolcoördinaten |
|||||
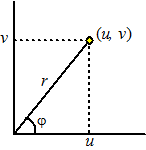
| Maar dat kunnen we
handiger doen door over te stappen op poolcoördinaten! Je kunt elk punt van dit eerste kwadrant ook aangeven met r (afstand tot de oorsprong) en φ (hoek met de x-as) Als je dan r van 0 naar ∞ laat lopen en φ van 0 naar 1/2π dan bereik je ook precies alle punten. Dan is u2 + v2 = r2 en u = rcosφ en v = rsinφ Het enige is die dudv. Dat is de oppervlakte van een rechthoekje van du bij dv Hoe wordt dat met r en φ? Dat kun je in deze les over de Jacobiaan vinden. De conclusie daar is dat dA = dudv verandert in = r • drdφ Dat geeft voor de integraal: |
|
||||
|
|
|||||
| Omdat die machten 2x
- 1 en 1 - 2x precies elkaars tegengestelde zijn vielen die r-machten
weg, en kon je die sinus en die cosinus samennemen tot een tangens. De binnenste integraal (voor de r-delen) is nu uit te rekenen: |
|||||
|
|
|||||
| Dan blijft er over: | |||||
|
|
|||||
|
derde substitutie. Als we nu nemen tanφ = 1/w dan is φ = arctan(1/w) en de grenzen lopen van w = ∞ naar w = 0, verder is: |
|||||
|
|
|||||
|
|
|||||
|
vierde
(en laatste) substitutie. Neem tenslotte w2 = t dus w = √t en dw = 1/2√t • dt |
|||||
|
|
|||||
| En nou nog even integreren,,,, | |||||
|
|
|||||
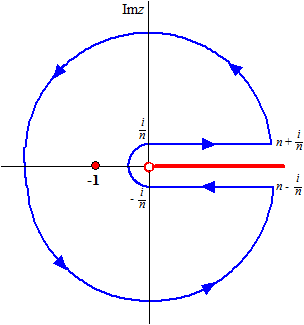
| Die integraal is nog
steeds niet zo makkelijk. We gaan hem uitvoeren met een contourintegraal
in het complexe vlak! Nou is het probleem dat die functie t x - 1 in het complexe vlak een meerwaardige functie is. Dat betekent simpelweg dat we niet vrijuit met onze integratieroute rondjes mogen maken, omdat de functie sprongen vertoond. Als we er maar voor zorgen dat onze integratieroute bijvoorbeeld de positieve x-as (reële as) niet overschrijdt dan is alle oké. Die rode lijn hiernaast is een muur! Of eigenlijk een gapend gat! Meer daarover staat in deze les. Kies de blauwe integratieroute hiernaast. Daarbij laten we n naar oneindig gaan. De route bestaat uit 4 delen; A. recht stuk van i/n naar n+i/n B. grote cirkel buitenom C. recht stuk van n-i/n naar -i/n D. klein half cirkeltje van -i/n naar i/n |
|||||
| Laten we die vier stukken apart gaan bekijken als n → ∞, dus als i/n → 0 : | |||||
|
A. |
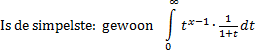 |
||||
| B. | Die gaat naar nul, want als |t| naar oneindig gaat, dan gaat die integrand naar nul! | ||||
| C. | De lastigste. Hier is de functie t x - 1 gelijk aan e2pix • t x - 1 en loopt hij van ∞ naar 0 | ||||
|
|
|||||
| D. | Die gaat naar nul, want als |t| naar nul gaat, gaat die integrand naar nul. | ||||
| Samen zijn al die
integralen gelijk aan de som van de residuen van deze contour. Nou is er slechts één singulier punt binnen de contour, namelijk x = -1, en het residu daarvan is -2πieπix want daarvoor moet je die noemer weglaten (die zorgt voor de singulariteit) en x = -1 invullen en dan krijg je het volgende: Res(-1) = 2πi • (-1)x - 1 = 2πiepi(x - 1) = -2πieπix Kortom, we houden over: |
|||||
|
|
|||||
|
|
|||||
|
|
|||||
| Conclusie: | |||||
|
|||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||