radialen


Radialen.	© h.hofstede (h.hofstede@hogeland.nl)

Een mooi vraagstuk uit de brugklas is altijd: "Welke van de volgende hoeken is het grootst?"

Gegarandeerd natuurlijk dat er een paar voor hoek C stemmen! Die ziet er ook het grootst uit immers?
Wij weten intussen dat het niet gaat om de lengte van de benen van een hoek. Dat zijn immers twee halve lijnen dus die zijn oneindig lang. Het gaat om de "tussenruimte".

De brugklasmethode was: verdeel een rechte hoek in 90 even grote stukjes (minihoekjes) en noem één zo'n stukje een "graad". Van een willekeurig hoek meet je dus gewoon hoeveel zulke stukjes van één graad er naast elkaar inpassen. Dat heet het aantal graden van een hoek.
Maar dit is eigenlijk nogal een rare, primitieve en willekeurige methode.
Waarom bijvoorbeeld 90? Waarom niet 38 of 145 of.....? Waar slaat dat op?

Heb jij die flauwekul ook altijd maar voor zoete koek aangenomen????

Er is een betere, wetenschappelijkere methode, en die heeft te maken met onze eenheidscirkel.
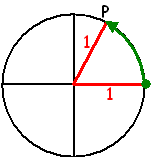
Spreek af, dat we hoeken voortaan tekenen met benen met allemaal lengte 1 (1 eenheid, dus dat kan cm zijn of m of inch of mijl.... dat doet er niet toe).
Dan past zo'n hoek precies in een eenheidscirkel.
Leg één been van de hoek langs de positieve x-as zoals bij de rode hoek hiernaast is gebeurd.
De grootte van de hoek is nu hoe ver punt P gedraaid is vanaf de positieve x-as.
De groene pijl geeft dat aan.
Hoe groter de hoek, des te langer de pijl. Daarom maken we de afspraak:

grootte van de hoek = lengte van de groene pijl.

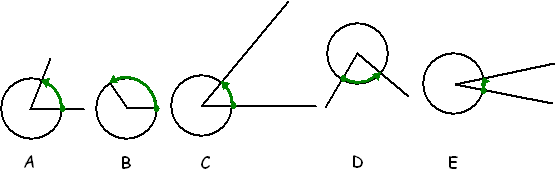
Hieronder zie je hoe dat werkt bij de hoeken A tm E bovenaan. Telkens is een eenheidscirkel getekend met als middelpunt het hoekpunt.

Geen twijfel mogelijk: hoek B heeft de langste groene pijl dus is het grootst. En hoek E de kortste dus die is het kleinst.
De nieuwe hoekeenheid heet niet graden maar "RADIALEN" en de afkorting is "rad".

Welke "Radialen" horen bij "Graden""?

Een hele cirkel heeft omtrek 2pr dus een cirkel met straal 1 heeft omtrek 2p. Maar omdat een hele cirkel gelijk is aan 360º moet gelden:

360º = 2π rad.

Om graden en radialen in elkaar om te rekenen kun je gewoon een verhoudingsschema gebruiken.
Dat gaat natuurlijk zo

Voorbeeld 1. Hoeveel radialen is een hoek van 50º?

Omdat 360º = 2π rad geeft dat het volgende verhoudingsschema:

graden	360	50
radialen	2π	??

Dat geeft al snel ?? = ^{50 • 2π}/₃₆₀ ≈ 0,87 rad.

Voorbeeld 2: Hoeveel graden is een hoek van 2,8 radialen?

Omdat 360º = 2π rad geeft dat het volgende verhoudingsschema:

graden	360	??
radialen	2π	2,8

Dat geeft al snel ?? = ^{2,8 • 360}/_2π ≈ 160,43º

Hieronder staan een aantal veel voorkomende hoeken in graden en in radialen.

graden	0	30	45	60	90	120	135	150	180	270	360
radialen	0	¹/₆π	¹/₄π	¹/₃π	¹/₂π	²/₃π	³/₄π	⁵/₆π	π	1¹/₂π	2π

We hebben overal de radialen in een aantal keer π laten staan. Je zou het ook natuurlijk gewoon kunnen uitrekenen. Dan zou bijvoorbeeld ¹/₂π rad gelijk zijn aan ongeveer 1,57 rad. Maar ja, dat laatste is afgerond en die π-aantallen zijn exact, dus dat hebben wiskundigen veel liever (eigenlijk veel veel veel veel veel veel veel veel liever).

OPGAVEN

Hoeveel graden is een hoek van 1 rad?

57,3º

Hoeveel radialen is een hoek van 1º?

^π/₁₈₀

Reken de volgende hoeken van graden om naar radialen.

40º

²/₉π

72º

²/₅π

400º

2²/₉π

138º

²³/₃₀π

250º

²⁵/₁₈π

102º

¹⁷/₃₀π

24º

²/₁₅π

-55º

-¹¹/₃₆π

-80º

-⁴/₉π

Reken de volgende hoeken van radialen om naar graden. Rond indien nodig af op gehele graden.

10 rad

573º

1¹/₈π rad

22,5º

3¹/₆π rad

570º

¹/₁₂p rad

15º

2,6 rad

149º

6,9 rad

395º

-3 rad

-172º

90 rad

5157º

22 rad

1261º

Bereken met je GR (de hoeken zijn in radialen) en rond indien nodig af op twee decimalen:

cos(²/₃π)

-0,5

d. sin(³/₇π)

0,97

g. tan(2)

-2,19

sin(-¹/₆π)

-0,5

e. tan(1²/₃π)

-1,73

h. cos(1,5)

0,07

tan(¹/₄π)

f. cos(-4¹/₅π)

0,81

i. sin(8,23)

0,93

De grote wijzer van een klok is 12 cm lang, en de kleine wijzer is 8 cm lang. Het is nu precies drie uur.

Welke afstand heeft het uiteinde van de grote wijzer afgelegd als het vijf voor half vijf is geworden?

34π

Hoe laat is het geworden als de kleine wijzer een afstand van 16 cm heeft afgelegd?
Geef je antwoord in minuten nauwkeurig.

6:49

Om 12 uur staan beide wijzers precies gelijk. Als α de hoek waarover de grote wijzer heeft gedraaid is (in radialen), en t de tijd in minuten vanaf 12 uur, dan geldt α = ^πt/₃₀

Toon aan dat die formule klopt, en leid ook zo'n formule voor de kleine wijzer af.

α = ^π^t/₃₆₀

Bereken met de formules uit vraag c) op welk tijdstip de wijzers voor het eerst na 12 uur wéér precies gelijkstaan. Geef je antwoord in seconden nauwkeurig.

13:05:27

Teken op onderstaande geo-driehoek de hoeken van 0, ¹/₆π, ¹/₄π, ¹/₃π, ¹/₂π, ²/₃π, ³/₄π, ⁵/₆π en π radialen.

Rangschik naar opklimmende grootte zonder je GR te gebruiken (de hoeken zijn uiteraard in radialen):
cos1 - cos2 - cos3 - cos4 - cos5

3-4-2-5-1