| |
 |
| |
ę h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Pythagore´sche drietallen. |
| |
|
|
|
Pythagore´sche drietallen zijn setjes van 3 gehele getallen waarvoor de stelling van Pythagoras geldt.
Een voorbeeld is 3 - 4 - 5 want 32 + 42
= 52
En dan zijn er natuurlijk meteen de flauwe andere drietallen:
6 - 8 - 10
9 - 12 - 15
12 - 16 - 20
15 - 20 - 25
enz.
Dat noemen we geen nieuwe drietallen, omdat je ze allemaal kunt
delen zodat er weer 3-4-5 uitkomt.
We zijn in deze les op zoek naar "originele" Pythagore´sche
drietallen.
Euclides had al een prachtige formule om zulke drietallen te vinden,
namelijk: |
| |
|
|
|
|
 |
| |
|
|
|
Dat dat inderdaad zo
is kun je natuurlijk makkelijk controleren, dat lukt me zelfs in ÚÚn
regel, kijk maar:
(m2 - n2)2 + (2mn)2
= (m4 - 2m2n2
+ n4 ) + 4m2n2
= m4 + 2m2n2 + n4
= (m2 + n2)2
q.e.d.
Een interessantere vraag is natuurljjk:
Hoe kˇm je d'r op??
Laten we het probleem a2 + b2
= c2 vertalen naar een meetkundig probleem. Dat
deden de Grieken eigenlijk zo vaak het maar kon. Misschien dat we dan
iets kunnen snappen of ontdekken van de gedachtengang van Euclides.
|
| |
|
|
|
x2
+ y2 = c2 is natuurlijk de
vergelijking van een cirkel met middelpunt de oorsprong en straal c.
(Daar in die driehoek stßßt natuurlijk gewoon de stelling van
Pythagoras met x2 + y2 = c2
)
Als je nou voor de straal van die cirkel een geheel getal neemt,
dan is c tenminste alvast geheel. De vraag "Welk drietal
(x, y, c) is een Pythagore´sch drietal?" is dan het zelfde als
de vraag: |
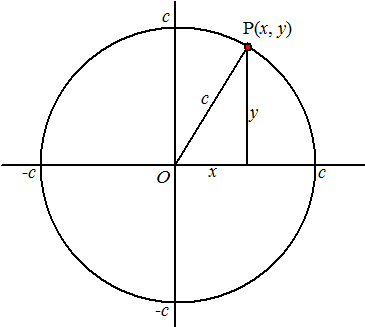 |
| |
|
|
| Welke roosterpunten (x, y) liggen op de
cirkel? |
|
| |
|
|
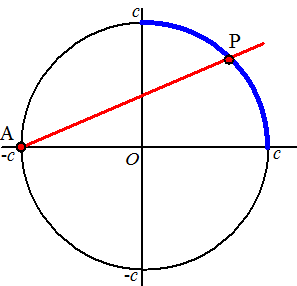
Nou is er een leuk
trucje om zulke roosterpunten te vinden, en dat staat hiernaast
uitgelegd.
Teken een rechte lijn door het punt (-c, 0) naar het blauwe
stuk van de cirkel. Die snijdt de cirkel in punt P.
Stel nu een formule op van die rechte lijn en bereken met die formule de
snijpunten met de cirkel. Dat geeft in iedere geval een kwadratische
vergelijking, en de oplossingen ervan kun je met de ABC-formule vinden.
Maar ÚÚn van die oplossingen is een geheel getal:
namelijk x = -c !
Dat betekent dat de discriminant van die ABC formule ook als geheel
kwadraat te schrijven is, dus is de tweede oplossing ˇˇk een getal
zonder wortels!!
Dus hebben we een punt P gevonden met een gehele x-co÷rdinaat
zonder wortels erin!!!
En de y heeft dan ook geen wortels, immers die vind je door x
in de rechte lijn formule in te vullen. |
 |
| |
|
|
|
Weet je wat! Laten we
eens gek doen: We gaan dit hele
verhaal gewoon UITVOEREN!
Een lijn door (-c, 0) heeft vergelijking y =
px + pc. Daarin is p een willekeurig getal. Het
stelt de helling van de rode lijn voor, dus als we straks een punt P op
het blauwe cirkelstuk willen hebben moeten we nemen 0 < p < 1
Snijpunt van y = px + pc met x2
+ y2 = c2 geeft:
x2 + (px + pc)2 = c2
x2 + p2x2 + 2p2cx
+ p2c2 - c2 = 0
x2(1 + p2) + 2p2cx
+ (p2c2 - c2)
= 0
Dat geeft een ABC-formule met discriminant D = (-2p2c)2
- 4 Ľ (1 + p2) Ľ (p2c2
- c2)
D = 4p4c2 - 4p4c2
+ 4c2 - 4p2c2
+ 4p2c2 = 4c2
√D = ▒√(4c2)
= ▒2c. Mooi: een
geheel getal. Dat moest ook!
De oplossingen van de ABC formule worden dan: x = (-2p▓c
▒ 2c)/2(1 + p▓)
= -c of c Ľ
(1 - p▓)/(1
+ p▓)
Die eerste is inderdaad zoals verwacht (gelukkig maar). Die tweede
geeft punt P.
Dan is yP = px + pc = pc Ľ
(1 - p▓)/(1 +
p▓) + 1) = pc Ľ
((1 - p▓)/(1
+ p▓) + (1 + p▓)/(1
+ p▓) = 2pc/(1
+ p▓)
Daarmee hebben we een Pythagore´sch drietal gevonden zonder wortels
erin: |
| |
|
|
|
(x, y,
c) is het drietal ( c Ľ (1 - p▓)/(1
+ p▓) ,
2pc/(1 + p▓)
, c)
Dat kun je nog vereenvoudigen door alle drie door c te delen en
met (1 + p2) te vermenigvuldigen: |
| |
|
|
|
|
(1 - p2),
(2p), (1 + p2) is
een Pythagore´sch drietal zonder wortels. |
|
| |
|
|
|
Neem nu p =
n/m, immers p was de helling van die
rode lijn, en die moest tussen 0 en 1 liggen. Die kun je dus schrijven
als n/m met n < m.
Dan vind je het drietal (1 - (n/m)2),
(2n/m), (1 + (n/m)2)
Om echte gehele getallen te krijgen vermenigvuldig je alles tenslotte
met m2
Dat geeft het drietal (m2 - n2),
(2mn), (m2 + n2)
Precies zoals Euclides hierboven al vond. Kies maar een m
en een n en je vindt een Pythagore´sch drietal.
Hier zijn er een aantal: |
| |
|
|
|
| |
m |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
n |
1 |
|
(3, 4, 5) |
(8, 6, 10)
|
(15, 8, 17) |
(24, 10, 26) |
(35, 12, 37) |
(48, 14, 50) |
| 2 |
|
|
(5, 12, 13) |
(12, 16, 20) |
(21, 20, 29) |
(32, 24, 40) |
(45, 28, 53) |
| 3 |
|
|
|
(7, 24, 25) |
(16, 30, 34) |
(27, 36, 45) |
(40, 42, 58) |
| 4 |
|
|
|
|
(9, 40, 41) |
(20, 48, 52) |
(33, 56, 65) |
| 5 |
|
|
|
|
|
(11, 60, 61) |
(24, 70, 74) |
| 6 |
|
|
|
|
|
|
(13, 84, 85) |
| 7 |
|
|
|
|
|
|
|
|
| |
|
|
|
|
Maar die zijn niet allemaal
"origineel".... |
| |
|
|
|
Dat klopt:
degenen met dezelfde kleur zijn eigenlijk gelijk aan elkaar.
Kunnen we van tevoren al zeggen of we een origineel drietal krijgen of
niet?
Kijk daarvoor naar de drie getallen m2 - n2
en 2mn en m2 + n2
Van 2mn weten we dat het een even getal is (Dűh:
er staat een 2 in!)
Maar dat betekent dat m2 - n2
NIET ˇˇk even mag zijn, want als dat zo is, dan is m2
+ n2 het ook (som van twee even getallen is even)
dus is het hele drietal door 2 te delen.
Conclusie: m2 - n2
moet oneven zijn.
Maar omdat m2 - n2 =
(m - n)(m + n) moeten die beide
getallen ˇˇk oneven zijn (een even getal ergens mee
vermenigvuldigen levert altijd weer een even getal op). Kortom: we
mogen alleen de m en n nemen die opgeteld een oneven getal
geven (Als m + n oneven is, dan is m - n
het ook want het verschil ertussen is 2n en dat is even). |
| |
|
|
|
|
|
| |
|
|
|
| Daarmee vallen een
groot aantal drietallen uit de tabel hierboven af. De helft om precies
te zijn: |
| |
|
|
|
| |
m |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
n |
1 |
|
(3, 4, 5) |
|
(15, 8, 17) |
|
(35, 12, 37) |
|
| 2 |
|
|
(5, 12, 13) |
|
(21, 20, 29) |
|
(45, 28, 53) |
| 3 |
|
|
|
(7, 24, 25) |
|
(27, 36, 45) |
|
| 4 |
|
|
|
|
(9, 40, 41) |
|
(33, 56, 65) |
| 5 |
|
|
|
|
|
(11, 60, 61) |
|
| 6 |
|
|
|
|
|
|
(13, 84, 85) |
| 7 |
|
|
|
|
|
|
|
|
| |
|
|
|
| Kijk: da's dan
weer mooi: Nou zijn er geen dubbelen meer!! |
| |
|
|
|
| |
|
|
|
| |
|
|
|
|
OPGAVEN |
| |
|
|
|
| 1. |
Drie cirkels met stralen 3, 5 en 12
raken elkaar zoals in de figuur hiernaast.
Hoe lang is de getekende boog? |
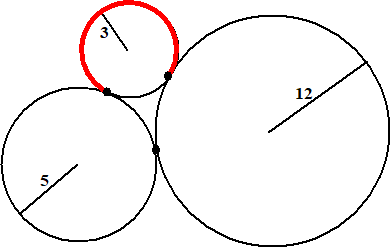 |
| |
|
|
|
| |
|
|
 |
| |
|
|
|
| |
|
|
|
|
| |
|
|
|
|
ę h.hofstede (h.hofstede@hogeland.nl)
|