| |
 |
|
Pythagore´sche drietallen. |
ę
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
|
|
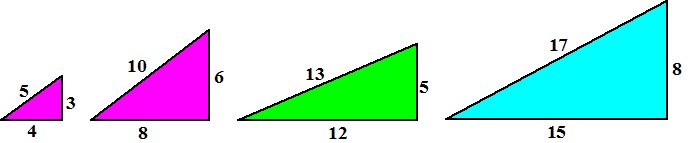
| Een Pythagore´sch drietal bestaat
uit drie gehele getallen a, b en c waarvoor
geldt a2 + b2 = c2
. De drie getallen zouden dus de drie zijden van een rechthoekige
driehoek kunnen zijn. Hier zie je er een paar: |
| |
|
|
|
|
 |
| |
|
|
|
Die eerste twee zijn nog
gelijkvormig, maar die anderen niet. Er blijken oneindig veel
verschillende Pythagore´sche drietallen te zijn. Maar hoe vind je ze?
|
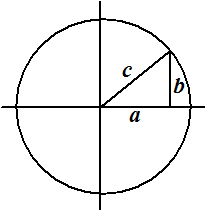
Nou is de vergelijking van een
cirkel met straal r en middelpunt O gelijk aan x2
+ y2 = r2. En dat is natuurlijk
precies de stelling van Pythagoras, maar dan met andere letters. Dat
betekent dat een rechthoekige driehoek met gehele zijden a, b
en c wiskundig gezien eigenlijk precies hetzelfde is als
een cirkel met middelpunt O en straal c, die door het
roosterpunt (a, b) gaat.
Door te schrijven (x/r)2
+ (y/r)2 = 1
brengen we het probleem terug tot het vinden van punten van de cirkel
x2 + y2 = 1 met als
co÷rdinaten breuken, Dan kun je er makkelijk een Pythagore´sch drietal
van maken. |
 |
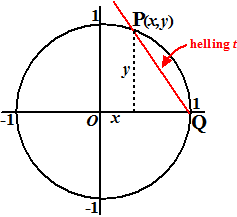
We gaan proberen voor
deze cirkel een parameterkromme te maken.
De truc daarvoor zie je hiernaast.
Laat de t die bij een willekeurig punt P van de cirkel
hoort gelijk zijn aan de helling PQ waarbij Q het punt (1,0) is. Dus een
lijn met helling t vanaf Q levert een snijpunt P met de cirkel
op. In de figuur hiernaast zie je dat, als t alle waarden
doorloopt, dat dan punt Q de cirkel doorloopt.
|
 |
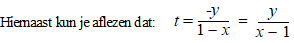 |
| Dat geeft y
= t(x - 1) |
Invullen in de
vergelijking van de cirkel: x2 + t2(x
- 1)2 = 1
⇒ x2
+ t2x2 - t22x
+ t2 - 1 = 0
⇒ x2 (1 + t2)
+ x(-2t2 ) + (t2
- 1) = 0
Nou, daar kun je de ABC-formule op loslaten: |
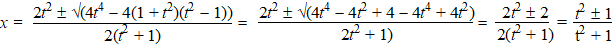 |
De oplossing met het
plusteken is saai: x = 1, en dat is natuurlijk punt Q.
De oplossing met het minteken is interessanter: |
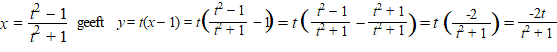 |
| Daarmee wordt de
parametervoorstelling van de cirkel: |
| |
|
|
|
|
|
| |
|
|
|
En het mooie van de
parametervoorstelling is, dat er alleen maar hele machten van t
in voorkomen.
Waarom dat zo mooi is?
Nou, als je voor t een geheel getal neemt, dan krijg je voor x
en y breuken, en daar kun je dan makkelijk een Pythagore´sch
drietal met gehele getallen van maken.
Neem bijvoorbeeld t = 2, dat geeft x = 3/5
en y = -4/5 dus
geldt (3/5)2 + (-4/5)2
= 1 dus 32 + 42 = 52
Het levert het Pythagore´sche drietal 3-4-5 op.
Hier is een lijstje met de drietallen die t = 1 t.m. 10
opleveren: |
| |
|
|
|
| t |
drietal |
vereenvoudigd |
| 1 |
0 - 2 - 2 |
0 - 1 - 1 |
| 2 |
3 - 4 - 5 |
3 - 4 - 5 |
| 3 |
6 - 8 - 10 |
3 - 4 - 5 |
| 4 |
8 - 15 - 17 |
8 - 15 - 17 |
| 5 |
10 - 24 - 26 |
5 - 12 - 13 |
| 6 |
12 - 35 - 37 |
12 - 35 - 37 |
| 7 |
14 - 48 - 50 |
7 - 24 - 25 |
| 8 |
16 - 63 - 65 |
16 - 63 - 65 |
| 9 |
18 - 80 - 82 |
9 - 40 - 41 |
| 10 |
20 - 99 -101 |
20 - 99 -101 |
|
| |
|
|
|
| En ga zo maar
door.... COOL toch?....... |
| |
|
|
|
|
ę
h.hofstede (h.hofstede@hogeland.nl) |
| |
|
|
|