|
|
 |
|
Puntenwolken. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
Er wordt nogal wat
onderzocht tegenwoordig.
En dat levert een boel rapporten en krantenkoppen op. |
| |
|
|
 |
| |
|
| Heel erg vaak (eigenlijk bijna
altijd) gaat het bij zo'n onderzoek over een verband tussen twee gemeten
grootheden. Er zijn gewoon stapels verbanden te onderzoeken!! |
| |
|
|
 |
| |
|
Als het gaat om een verband
tussen twee dingen, en als we die dingen bovendien
getallen kunnen uitdrukken, dan kunnen wij als wiskundigen daar
natuurlijk makkelijk een plaatje van maken! Zet het ene ding op de x-as
en het andere ding op de y-as en je kunt al je metingen met een
stip aangeven.
Hoogste tijd voor een voorbeeld.....
In de volgende tabel staat voor de 16 leerlingen van een 4-HAVO klas
hoeveel tijd zij gemiddeld aan hun huiswerk besteden, en ook wat hun
rapportcijfer op wiskunde is. |
| |
|
| huiswerktijd (min) |
0 |
11 |
16 |
28 |
28 |
36 |
39 |
46 |
47 |
49 |
55 |
58 |
63 |
68 |
79 |
95 |
| wiskundecijfer |
3.0 |
4.0 |
6.0 |
4.2 |
6.5 |
5.9 |
7.7 |
4.8 |
7.1 |
8.3 |
5.8 |
7.8 |
9.0 |
7.7 |
8.6 |
9.3 |
|
| |
|
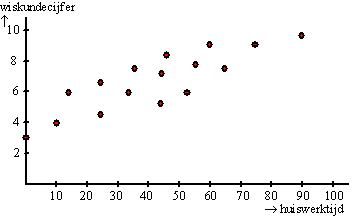
Hiernaast staat op de x-as de
huiswerktijd en op de y-as het wiskundecijfer. Dat geeft een hele
serie van punten. Een diagram als hiernaast heet een
spreidingsdiagram, en zo'n serie van
punten noemen we een puntenwolk.
De grote vraag is nu: "Is er een verband tussen het cijfer en de
huiswerktijd?". En zo ja: wat is dat verband dan, en hoe sterk is dat
verband?
Zo'n verband noemen we een correlatie.
Het antwoord op al deze vragen is: dat hangt af van de vorm van de
puntenwolk.
Laten we een paar mogelijke puntenwolk-vormen bekijken: |
 |
| |
|
|
 |
| |
|
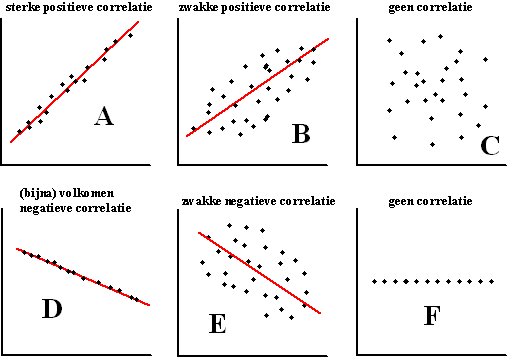
Bij al deze figuren is op het oog
zo goed mogelijk een rechte lijn getekend. Die lijn, die het beste past
bij de puntenwolk, heet de regressielijn.
Later komen we daar nog uitgebreid op terug.
Twee dingen vallen verder op:
| |
|
| 1. |
We spreken van negatieve correlatie
als de regressielijn dalend is, en van positieve correlatie
als de regressielijn stijgend is. Dat klinkt logisch, immers als de
regressielijn daalt, dan neemt y af als x toeneemt. En
als een toename van de ene grootheid een afname van de andere
betekent, dan beÔnvloeden ze elkaar "negatief". A en B hierboven
horen bij positieve correlatie, D en E bij negatieve
correlatie. |
| |
|
| 2. |
Hoe meer de puntenwolk op een rechte lijn lijkt,
des te sterker is de correlatie. Als de punten exact op een rechte
lijn liggen (zoals bijna bij D) heet de correlatie
volkomen. Als de punten "willekeurig" verspreid liggen
(zoals bij C) is er geen correlatie. Merk nog op dat
we ook bij F spreken van geen correlatie: de y-waarden
variŽren helemaal niet, en lijken dus onafhankelijk van de
x-waarden. |
| |
|
|
| |
|
 |
| |
|
Invloed van de schaalverdeling |
| |
|
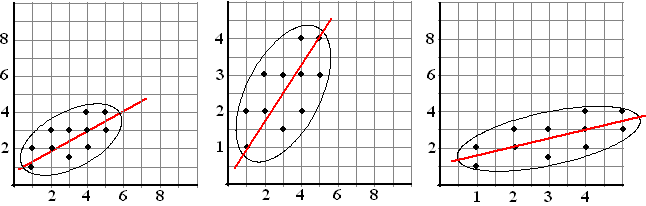
| Om dingen als sterkere of
zwakkere correlatie af te kunnen lezen uit een spreidingsdiagram is de
schaalverdeling op de x-as en de y-as wel van belang. Neem
de twee figuren hieronder. Daar staan drie keer precies dezelfde
meetwaarden uitgezet, maar met verschillende eenheden op de assen. |
| |
|
|
 |
| |
|
| De vorm van de wolken, en dus ook
de mate van correlatie, lijkt nogal verschillend. Terwijl het echt
precies dezelfde punten zijn! Om dit soort effecten te voorkomen kiezen
we meestal de schaal op de assen zů, dat bij de spreiding van x
en y (dus bij de standaarddeviatie!) even lange lijnstukken
horen. |
| |
|
| |
|
|
OPGAVEN |
| |
|
| 1. |
In de volgende tabel staat voor een echtparen de
lengte van de man en de lengte van de vrouw (in cm). |
| |
|
|
|
| |
| koppel nr. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| man |
196 |
208 |
174 |
163 |
186 |
171 |
172 |
160 |
201 |
184 |
168 |
182 |
| vrouw |
170 |
186 |
175 |
152 |
175 |
166 |
153 |
158 |
179 |
165 |
161 |
170 |
|
| |
|
|
|
| |
a. |
Teken een puntenwolk die bij deze gegevens past.
|
|
| |
|
|
|
| |
We gaan nu aan partnerruil
doen...... |
| |
|
|
|
| |
b. |
Schrijf de lengtes van de
vrouwen op losse briefjes. Vouw die op en gooi ze in een hoge
hoed of op een andere willekeurige stapel. Trek de briefjes ťťn
voor ťťn en koppel ze op die manier aan de mannen (briefje 1 bij
man 1, enz.).
Teken opnieuw een puntenwolk. |
| |
|
|
|
| |
c. |
Welke verschillen zie je in de
puntenwolken van vraag a) en vraag b)?
Wat zegt dat over de lengte van een man en de lengte van zijn
echtgenote? |
| |
|
|
|
| 2. |
Denk je dat er in de volgende
gevallen sprake is van sterke/zwakke en positieve/negatieve correlatie? |
| |
|
|
|
| |
a. |
De waarde van een auto en zijn
ouderdom. |
| |
b. |
Aantal ooievaars en aantal geboorten
in een gebied. |
| |
c. |
Aantal MacDonalds-vestigingen en
Bruto Nationaal Inkomen in een land. |
| |
d. |
Het aantal pasgeboren poesjes in een
nest en hun gemiddelde gewicht. |
| |
e. |
Leeftijd en bloeddruk. |
| |
f. |
Gezichtsvermogen en schoenmaat. |
| |
g. |
Het bouwjaar en het benzineverbruik
van een auto. |
| |
h. |
Aantal inbraken en aantal
verkeerslichten in de steden van Nederland dit afgelopen jaar. |
| |
|
|
|
| 3. |
Hieronder
staat een tabel voor de hoeveelheid vet, vezels en calorieŽn
voor 100 gram van een aantal voedingsmiddelen (bron:
calorielijst.nl). |
| |
|
|
|
| |
| voedsel |
vet |
koolhydraten |
caloriŽen |
| yoghurt |
4,9 |
17,9 |
127 |
| dieetmargarine (Aldi) |
60 |
0,2 |
541 |
| gekookte aardappelen |
0,1 |
17,0 |
78 |
| leverworst |
20,4 |
5,2 |
264 |
| honingmosterd (HEMA) |
10,3 |
15,6 |
182 |
| kaas 45+ |
31,0 |
2,0 |
400 |
| kipnuggets (AH) |
14,0 |
16,0 |
240 |
| M&M met pinda's |
27,1 |
57,3 |
514 |
| falafel |
12,5 |
27,0 |
263 |
| Fanta medium (McDonalds) |
0,0 |
48,0 |
190 |
| haaskarbonade |
6,7 |
0,0 |
150 |
|
| |
|
|
|
| |
Maak hiervan twee puntenwolken,
eentje met op de x-as de koolhydraten en op de y-as
de calorieŽn, en een tweede met op de x-as het vet en op
de y-as de calorieŽn.
Welke twee variabelen vertonen de grootste correlatie? |
| |
|
|
|
| |
|
|
 |
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|