principe van Fermat


Het principe van Fermat.	© h.hofstede (h.hofstede@hogeland.nl)

Licht dat door het ene materiaal gaat heeft een andere snelheid dan licht dat door een ander materiaal gaat. Dat heeft tot gevolg dat een lichtstraal breking vertoont als hij van het ene naar het andere materiaal gaat. De invallende lichtstraal en de uittredende lichtstraal maken een hoek met elkaar. Dat zie je hiernaast.

De normaal dat is die stippellijn hiernaast, die loodrecht op het grensvlak van beide materialen staat.

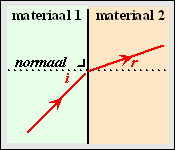Als een lichtstraal van dichter naar dunner materiaal gaat dan is er breking van de normaal af. Als hij van dunner naar dichter materiaal gaat is er breking naar de normaal toe (zoals in de tekening hiernaast: r < i )

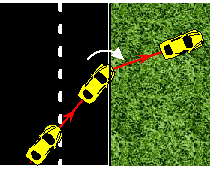
Ik hoop dat je dat logisch vindt:

Als je in een autootje op de snelweg rijdt en ineens gaat je rechtervoorwiel minder snel (omdat je daarmee in de berm raakt of zoiets) dan krijgt je autootje een afwijking naar rechts (zie hiernaast), omdat de rest van de wielen wél even snel blijft rijden.

De vraag is: "Wat is het verband tussen de hoeken i en r ?"

Een intelligente lichtstraal.

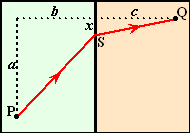
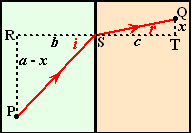
Oké, als jij nou een lichtstraal was, en je moest in de figuur hiernaast van punt P naar punt Q gaan, en je wilde dat graag zo snel mogelijk doen, hoe zou je dat dan doen?

Neem de afmetingen a, b en c als hiernaast, en stel dat jouw snelheid over route PS gelijk is aan v₁ en over SQ gelijk aan v₂.
Dan is de vraag dus: "waar moet je punt S kiezen?" Ofwel:

Hoe groot moet x zijn zodat de totale tijd minimaal is?

Kijk, en bij zo'n vraag veren wij wiskundigen weer op!!!
De totale tijd minimaal betekent dus dat de afgeleide ervan nul moet zijn. Daarom gaan we een formule voor die totale tijd opstellen, en die dan differentiëren en nulstellen. Dat is vertrouwd terrein voor ons.

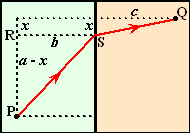
Als x de afstand in de figuur hiernaast is, dan geldt PR = a- x

Tweemaal Pythagoras:
x² + c² = SQ² dus SQ = √(x² + c²)
b² + (a - x)² = PS² dus PS = √(b² + (a - x)²)

tijd = afstand/snelheid, dus t_PQ = ^PS/_v1 en t_SQ = ^SQ/_v2
Met de twee Pythagorassen hierboven geeft dat voor de totale tijd over route PSQ:

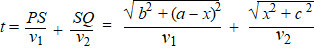Nu de afgeleide nul stellen (bedenk dat de afgeleide van √x gelijk is aan ¹/_(2√x) en vergeet de kettingregel niet).

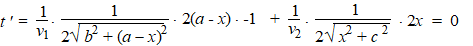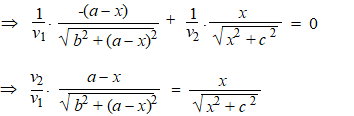Daar staan allemaal bekende afstanden uit de figuur hiernaast:

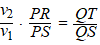De sinus in een rechthoekige driehoek is de overstaande rechthoekszijde gedeeld door de schuine zijde, dus:

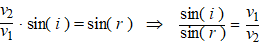En daar staat een beroemde natuurkundewet. De wet van Snellius. Als je de verhouding ^v1/_v2 gelijk stelt aan n (de brekingsindex heet dat) dan luidt de wet van Snellius:

maar wacht eens even.....

We zijn hierboven begonnen alsof wij een intelligente lichtstraal zijn die zo snel mogelijk van P naar Q moet gaan.
En verdomd!! Het blijkt dat lichtstralen dat inderdaad zo doen!!!

Dat heet het principe van Fermat:

lichtstralen volgen de route die de minste tijd kost

Ze kiezen dus gewoon precies de hierboven berekende route.
En ze doen dat ook nog eens vele malen sneller dan wij met al onze berekeningen! (met de lichtsnelheid namelijk)
Zijn lichtstralen soms intelligent????
Zijn het eigenlijk ALIENS....?????