Primitiveren (1).

© h.hofstede (h.hofstede@hogeland.nl)
Om de oppervlakte onder een grafiek van een functie f  uit te rekenen ontdekten we de volgende regel:

Maar om deze succesvol te gebruiken moet je natuurlijk wél die functie F kunnen bepalen. Die heet een primitieve van f en zo'n functie opstellen noemen we primitiveren. Eerder ontdekten we:   F' = f  

Primitiveren is dus eigenlijk "terug-differentiëren".

Deze opmerking is waarschijnlijk belangrijker dan je denkt. Het betekent namelijk het volgende:

Als je denkt een primitieve van f gevonden te hebben
dan kun je altijd je poging controleren door te differentiëren.
Dan moet immers f de uitkomst zijn.

Met machten gaat de gedachtegang ongeveer als volgt:

Hier is een lijstje van wat deze gedachtegang ons oplevert:
functie primitieve
x 1/2x2
x2 1/3x3
x3 1/4x4
x4 1/5x5
x5 1/6x6
Daar in dat rechterrijtje zie je natuurlijk de regelmaat wel!
Dat rijtje schreeuwt het uit:   "Maak een formule van mij!" "Maak een formule van mij!!"....
Die constante c staat er voor de volledigheid bij. We hebben al gezien dat je hem voor alle berekeningen best gelijk aan nul mag nemen.

Als er nog iets bij xn staat
• axn
Zo'n constante factor a schreef je bij differentiëren gewoon over, dus bij primitiveren óók!
voorbeeld:   f(x) = 3x4  geeft  F(x) = 3 • 1/5x5
• xn + a
Kijk uit!!! De primitieve van een constant getal is NIET NUL! Je zoekt immers een functie die a oplevert als hij wordt gedifferentieerd. En dat is ax.
voorbeeld:  f(x) = x2 + 3  geeft  F(x) = 1/3x3 + 3x
• xn + xm
Meerder losse termen mag je gewoon apart primitiveren (net zoals je ze vroeger apart mocht differentiëren). Hier staan dus eigenlijk twee losse opgaven.
voorbeeld:  f(x) =  x2 + 2x3   geeft  F(x) = 1/3x3 + 2 • 1/4x4       
1. Geef een primitieve functie van:
a. f(x) = 4x5 d. f(x) = x6 + 2x4
b. f(x) = 2x2 - 4x e. f(x) = 3 - 2x5 + x
c. f(x) = 1/2x4 + 3 f. f(x) = (2x + 3)2     (pas op!!)
2. Bereken algebraïsch de oppervlakten onder de volgende grafieken:
a. y = 6x - x2   tussen  x = 0 en x = 6.

36
b. y = 4x + 3 tussen x = 2 en x = 5.

51
c. y = x4 - 6x2 + 4x +10  tussen x = 0 en x = 4.

148,8
Vreemdere machten...
De regel om xn te primitiveren is een erg machtige. Je kunt er namelijk (bijna) alle machten mee primitiveren, ook als n geen geheel getal is. Dus ook:

•

 √x = x0,5  en de primitieve wordt  met de regel  1/1,5 • x1,5 =  2/3x√x
En dan natuurlijk ook dingen als  x√x = x1,5 met als primitieve  1/2,5 • x2,5 = 2/5x2√x

•

 1/x2 = x -2  en de primitieve wordt met de regel  1/-1 • x-1  = -1/x
En dan natuurlijk ook dingen als  1/x3 = x -3  enz.
Er is eigenlijk maar één macht van x die niet wil, en dat is  x-1 .
Als je onze geweldige regel namelijk op x-1 toepast krijg je  1/0 • x0 , en zoals je wel zult weten mag je niet door nul delen, dus die 1/0 is streng verboden. Hoe x-1 dan wél moet zullen we later nog zien......

Complicaties...

Denk erom dat je haakjes eerst wegwerkt en grotere breuken eerst vereenvoudigt.
Twee voorbeeldjes zullen duidelijk maken hoe het werkt:

•

 f(x) = x2 (x - √x)
Voor je kunt primitiveren moeten eerst de haakjes weg:  f(x) = x2 • x - x2 • √x = x3 - x2,5
Dat geeft primitieve:  F(x) = 1/4x4 - 1/3,5x3,5 = 1/4x4 - 2/7x3√x

•
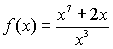
Voor je kunt primitiveren moet eerst de breuk weg: 
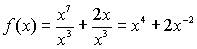Dat geeft primitieve  F(x) = 1/5x5 + 2 • 1/-1x-1 =  1/5x5 - 2/x
3. Geef een primitieve functie van:
a. f(x) = 5√x + 2x d. f(x) = 1/√x
b. f(x) = 4/x3 + 2/x2 e. f(x) = 2x√x + 5/x3 - 1
c. f(x) = 1 - x2√x f. f(x) = x4  - x4√x 

4. Geef een primitieve functie van:
a. f(x) = (x2 - 1)(√x + x) c. x4 • (x2 - 1/x3)
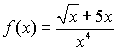
b. d.

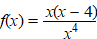5. Bereken algebraïsch de oppervlakten onder de volgende grafieken:
a. f(x) = 2 + 2√x  tussen x = 0 en x = 9.

54
b. f(x) = 4/x2   tussen x = 1 en x = 2.

2
c.

11,25
6. examenvraagstuk VWO, 1984.
     
  Met domein R+ ∪ {0} is gegeven de functie  f:  x →  x2 - 4x√x + 4x
Bereken de oppervlakte van het vlakdeel ingesloten door de grafiek van f en de x-as.
     
7. examenvraagstuk VWO, Wiskunde B, 2013.
     
  De functies f en g zijn gegeven door f (x) = (x2 - 1)(x - 11/2)
en  g(x) = -x + 11/2
In de figuur zijn de grafieken van f en g getekend.
De grafiek van f verdeelt driehoek OAB in twee delen.

Toon met een exacte berekening aan dat de oppervlakte van het linkerdeel twee keer zo groot is als de oppervlakte van het rechterdeel.
     
8. examenvraagstuk VWO, Wiskunde B, 2014.
     
  Voor x ≥ 0 is de functie f gegeven door f (x) = 3√x - x
De punten O(0, 0) en A(9, 0) liggen op de grafiek van f.
Het punt T is het hoogste punt van deze grafiek. Zie de figuur
De coördinaten van T zijn (21/4, 21/4).
   
  a. Toon dat aan
     
  V is het vlakdeel dat wordt begrensd door de grafiek van f en de x-as. In de figuur hiernaast is V grijs gemaakt.
  De lijn door A en T snijdt de y-as in het punt B. In de figuur hiernaast is driehoek OAB grijs gemaakt.
  b. Toon aan dat de oppervlakte van V en de oppervlakte van driehoek OAB gelijk zijn..
     
9. Gegeven is de functie f(x) = x3 - x
Geef twee functies die primitieven van f zijn en waarvan de grafiek de x-as raakt.
     
10. Examenvraagstuk VWO Wiskunde B, 2022-I
     
  De functie f is gegeven door  f(x) = x2 - 2x√x + x  met x ≥ 0 .

Bereken exact de oppervlakte van het vlakdeel ingesloten door de grafiek van f en de x-as.
   

1/30
     
   

© h.hofstede (h.hofstede@hogeland.nl)