| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Nog een paar primitieven. |
| |
|
|
|
Dit wordt één van de
makkelijker en ook kortere lesjes uit deze serie.
Misschien zelfs wel een onnodig lesje, want we gaan een paar primitieven
bekijken die je zelf waarschijnlijk ook wel kunt vinden.
Het draait allemaal uiteraard om de volgende regel: |
| |
|
|
|
|
F is een
primitieve van f ⇔ F' =
f |
|
| |
|
|
|
In "normaal"
Nederlands:
"Als je de primitieve van een functie f zoekt, dan zoek je een
functie waarvan f de afgeleide is"
(alhoewel, nu ik dit noteer realiseer ik me dat veel mensen dit
waarschijnlijk geen normaal Nederlands zullen vinden.)
De primitieve van xn hebben we al behandeld. Laten
we de regel op drie nieuwe functies gaan toepassen.
De primitieve van f(x)
= sinx
Oké, de vraag is dus eigenlijk: "van welke functie is sinx
de afgeleide?"
Je kunt je misschien nog wel herinneren dat sin en cosx een
"soort van" elkaars afgeleides waren. "Soort van", omdat het soms een
minteken scheelt.
Is F(x) = cosx misschien de primitieve van
f(x) = sinx?
Als dat zo is, dan zou de afgeleide van cosx gelijk moeten
zijn aan sinx, maar dat is niet zo! Die afgeleide is -sinx.
Nou, da's makkeljik te repareren: zet er gewoon een mintelen bij, en
alles komt goed! |
| |
|
|
|
|
de
primitieve van f(x) = sinx
is F(x) = -cosx |
|
| |
|
|
|
En voordat ik weer
boze emails krijg van mensen die "wel weten waar ik woon": daar
moet natuurlijk eigenlijk staan F(x) = -cosx + c
want de primitieve is op een constante na bepaald.
Nou, laten we dan meteen maar de primitieven van f(x) =
cosx doen. |
| |
|
|
|
|
de primitieve van
f(x) = cosx is F(x)
= sinx |
|
| |
|
|
|
| Je ziet dat hier het
minteken niet nodig is, want de afgeleide van sinx is
gewoon cosx (zonder minteken). En ook hier weer op een constante
c na bepaald natuurlijk.
De primitieve van f(x)
= gx |
| |
|
|
|
Tja: van welke
functie is gx de afgeleide??????
Nou, om eerllijk te zijn.....gx lijkt
nogal op zijn EIGEN afgeleide!!!!
De afgeleide van gx is namelijk
gx • lng en die lng is natuurlijk
gewoon een constante. Dus gx is op een
constante na gelijk aan zijn eigen afgeleide.
Als je de functie f(x) = (1/lng)
• gx neemt, dan valt die constante bij
het differentiëren weg en hou je vanzelf gx over. |
| |
|
|
|
|
|
| |
|
|
|
| En daarbij hebben we
dan direct het spediale geval van g = e. Dan is
lng = lne = 1 en is de functie gelijk aan zijn eigen
primitieve (en dus ook aan zijn eigen afgeleide) |
| |
|
|
|
| De primitieve van f(x)
= ex is
F(x) = ex |
|
| |
|
|
|
| Hoogste tijd om deze
nieuwe primitieven te gaan toepassen in wat opgaven. |
| |
|
|
|
|
OPGAVEN |
| |
|
|
|
| 1. |
Examenopgave VWO Wiskunde B,
2017-II |
| |
|
|
|
| |
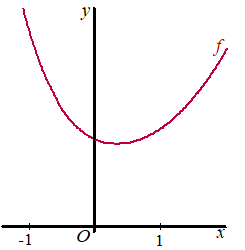
De functie f is gegeven door:
f (x) = 2x
+ 2-2x
In de figuur hiernaast is een deel van de grafiek van f
weergegeven.
De functie heeft één extreme waarde
en dat is een minimum. |
 |
| |
|
|
| |
a. |
Bereken exact de waarde van
x waarvoor f(x) minimaal is. |
| |
|
|
|
| |
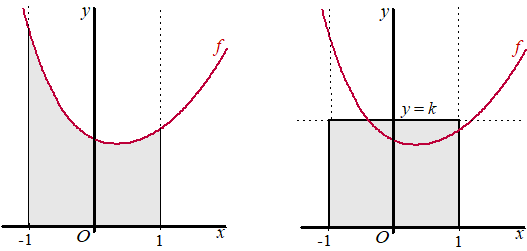
In de figuur linksonder is het gebied grijs
gemaakt dat wordt begrensd door de grafiek van f , de x-as
en de lijnen met vergelijkingen x = -1 en x = 1. In de
figuur rechtsonder is het rechthoekige gebied grijs gemaakt dat wordt
begrensd door de x-as en de lijnen met vergelijkingen x =
-1, x = 1 en y =
k .
De waarde van k is zo gekozen dat het grijze gebied uit beide
figuren dezelfde oppervlakte hebben. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
b. |
Bereken algebraïsch de waarde van k. Rond je
eindantwoord af op twee decimalen. |
| |
|
|
|
| |
|
|
|
| 2. |
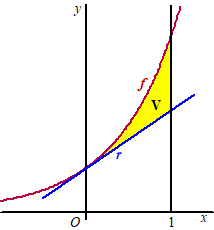
Aan de
grafiek van f(x) = gx
wordt de raaklijn r in het snijpunt met de
y-as getekend. Zie de figuur.
V is het vlakdeel, ingesloten door de grafiek van f, de
raaklijn r en de lijn x = 1.
Bereken voor welke g de oppervlakte van V gelijk is aan
1. Geef he antwoord in twee decimalen nauwkeurig.
|
 |
| |
|
|
|
| |
|
|
|
| 3. |
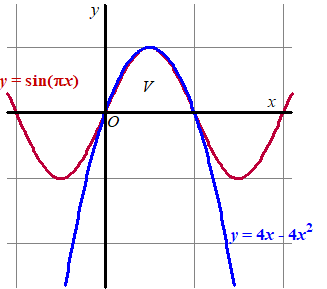
De grafiek
van y = 4x - 4x2 lijkt voor 0 ≤
x ≤ 1 nogal op de
grafiek van y = sin(πx).
Zie de figuur hiernaast.
Als je voor beide grafieken de oppervlakte V tussen
x = 0 en x = 1 en de x-as berekent,
kun je een benadering voor
π maken.
Hoe groot is die benadering?
|
 |
| |
|
|
|
| |
|
|
|
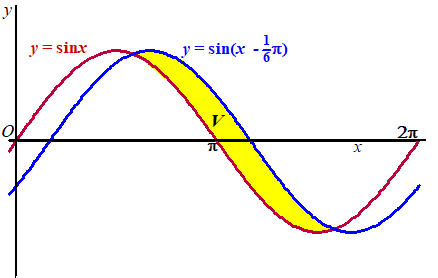
| 4. |
Als je de
grafiek van y = sinx over een afstand
1/6π
naar rechts schuift krijg je de grafiek van y =
sin(x - 1/6π)
Zie de figuur |
| |
|
|
|
| |
 |
| |
|
|
|
| |
a. |
Bereken
algebraïsch de oppervlakte van het gebied V dat wordt ingesloten
door deze beide grafieken.
Geef je antwoord in drie decimalen nauwkeurig.
Beperk je tot het deel waar 0 ≤ x ≤
2π |
| |
|
|
|
| |
In plaats
van 1/6π
kun je de grafiek van y = sinx natuurlijk over een
andere afstand a ( met 0 < a <
π) naar rechts schuiven.
Voor de oppervlakte O tussen beide grafieken
geldt dan O = 4sin(1/2a) |
| |
|
|
|
| |
b. |
Toon dat
aan. |
| |
|
|
|
| 5. |
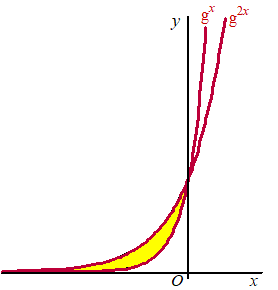
Gegeven
zijn de functies f (x) = gx
en h(x) = g2x
We bekijken het vlakdeel tussen beide grafieken voor x
< 0
Dat is aan de linkerkant niet begrensd, dus je er niet zomaar de
oppervlakte van uitrekenen.
Zie de figuur hiernaast.
Voor de oppervlakte (O) van het vlakdeel, ingesloten door
de grafieken van f en h en de lijn x = -a
geldt: |
 |
| |
|
|
| |
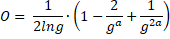
|
| |
|
|
| |
a. |
Toon dat aan. |
| |
|
|
|
| |
b. |
Voor welke
g wordt de (onbegrensde) oppervlakte tussen beide
grafieken voor x < 0 gelijk aan 1? |
| |
|
|
|
| 6. |
Examenvraagstuk VWO Wiskunde B, 2023-I
De functie f
wordt gegeven door f(x) = | sinx
+ 1/2√3
|
In de figuur is de grafiek van f als zwarte lijn
weergegeven. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
In de
figuur zijn de toppen A en B van de grafiek van
f aangegeven. A en B zijn de toppen die horen
bij de eerste twee maxima van f rechts van de y-as.
Er bestaat een sinusoïde die gegeven wordt door g(x)
= a + bsin(x), waarvan twee opeenvolgende
toppen samenvallen met de punten A en B. De
grafiek van g is in de figuur rood weergegeven. |
| |
|
|
|
| |
a. |
Bereken exact de waarde
van a en b. |
| |
|
|
|
| |
De grafiek
van f en de x-as sluiten twee soorten vlakdelen
in: kleine vlakdelen en grote vlakdelen. In de figuur is een van
de kleine vlakdelen grijs gemaakt. |
| |
|
|
|
| |
b. |
Bereken exact de
oppervlakte van een klein vlakdeel. |
| |
|
|
|
| |
|
|
 |
|
| |
|
|
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|