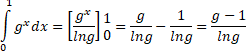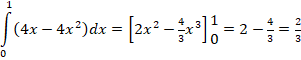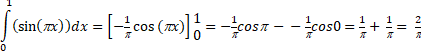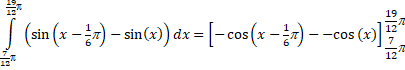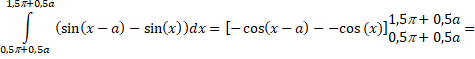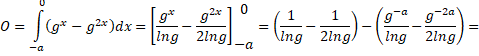© h.hofstede (h.hofstede@hogeland.nl)

 
1. a. Dan is de afgeleide nul.
f ' = 2x • ln2 + 2-2x • ln2 • -2 = 0
ln2 • (2x - 2 • 2-2x) = 0
2x - 2 • 2-2x = 0
2x  = 2 • 2-2x
2x = 2-2x + 1 
x = -2x + 1
3x = 1
x = 1/3.
       
  b. De oppervlakte in de linkerfiguur:
   
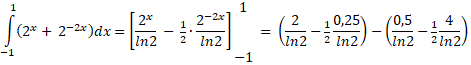    = 1/ln2 • (2 - 1/8 - 1/2 + 2) = 1/ln2 • 27/8 ≈ 4,8691

De oppervlakte rechts is  2k
2k = 4,8691  geeft  k ≈ 2,43
       
2. f '(x) = gx • lng  dus  f ' (0) = lng
De raaklijn is de lijn   y = lng • x + 1
De oppervlakte onder de raaklijn tussen x = 0 en x = 1 is dan  1 + 1/2lng

De oppervlakte onder de grafiek van f tussen x = 0 en x = 1 is gelijk aan:
 

       
  V heeft oppervlakte   (g - 1)/lng - 1 - 1/2lng
Y1 =  (X - 1)/ln(X)-1-0,5ln(X)
Y2 = 1
intersect geeft  X = g = 6,49
       
3.

 

  Als dat ongeveer gelijk is, dan is  π ≈ 3
       
4. a. snijpunten:
sinx = sin(x - 1/6π)
x = x - 1/6π + k2π  ∨  x = π - x + 1/6π + k2π
(vervalt)  ∨   2x = 7/6π + k2π
x = 7/12π + kπ
Dat geeft de snijpunten  x = 7/12π  en  x = 17/12π
       
   

    = {-cos(17/12π) + cos(19/12π)} - {-cos(5/12π) + cos(7/12π)}
= -cos(17/12π) + cos(19/12π) + cos(5/12π) - cos(7/12π)
= 1,035
     
  b. snijpunten:
sinx = sin(x - a)
x = x - a + k2π  ∨  x = π -  x + a + k2π
vervalt)  ∨   2x = π + a + k2π
x = 1/2π + 1/2a + kπ
Dat geeft de snijpunten  x = 1/2π + 1/2a  en  x = 11/2π + 1/2a
       
   

    = {-cos(1,5π - 0,5a) + cos(1,5π + 0,5a)} - {-cos(0,5π - 0,5a) + cos(0,5π + 0,5a)}

Gebruik nu:
cos(1,5π - x) = -sinx
cos(1,5π + x) = sinx
cos(0,5π + x) = -sinx
cos(0,5π - x) = sinx

Dat geeft:
O = --sin(0,5a) +  sin(0,5a) + sin(0,5a) + sin(0,5a)
O = 4sin(1/2a)
       
5. a.

    = 1/2lng • (2 - 1 - 2g-a + g-2a )
   

       
  b. Als a naar oneindig gaat, dan gaan de tweede en derde term tussen de haakjes beiden naar nul.
Die worden dus te verwaarlozen ten opzichte van de  1.
De oppervlakte wordt dus  1/2lng

1/2lng = 1  betekent lng = 1/2  dus g = √e
       
6. a. A ligt bij  x = 1/2π  dus yA = 1 + 1/2√3
B ligt bij  x = 3/2π  dus yB =  |-1 + 1/2√3| = 1 - 1/2√3
de evenwichtlijn van de grafiek van g ligt midden tussen deze twee y-waarden in, dus bij  y = 1 
dus a = 1
b is de amplitude en die is gelijk aan  b = 1/2√3
       
  b. |sinx + 1/2√3| = 0
sinx + 1/2√3 = 0
sinx = -1/2√3
x = 4/3p  (+ k2p)  ∨  x = 5/3p  (+ k2p)
De oppervlakte is dan:  (minteken omdat de grafiek van y = sinx + 1/2√3  onder de x-as ligt)
   
    = -{(-0,5 + 1/2√3 • 5/3p) - (0,5 + 1/2√3 • 4/3p)}
= 0,5 - 5/3p√3 -+0,5 + 4/6p√3
= 1 - 1/6p√3
       

© h.hofstede (h.hofstede@hogeland.nl)