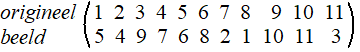© h.hofstede (h.hofstede@hogeland.nl)

Permutatiegroepen.
       
We zagen in een vorige les al dat we een bijectie van een groep met een eindig aantal elementen kunnen schrijven als een permutatie. Bijvoorbeeld:
 

       
Daar staat een afbeelding met bijv.  f (3) = 9 en  f (8) = 1

Als we een verzameling van 3 elementen {1, 2, 3} nemen dan hebben we bijvoorbeeld de permutatie f(1) = 2, f(2) = 3 en
f(3) = 1  maar ook de permutatie  g(1) = 1, g(2) = 3 en g(3) = 2
We kunnen het dan zelfs hebben over  g(f(x))  ofwel  (g o f )(x) en die noteren we als volgt:
       
       
Let erop in die laatste notatie dat de rechter permutatie eerst komt, en daarna pas de linker.
Natuurlijk kunnen we die laatste samengestelde permutatie ook wel weer als één afbeelding schrijven:
       

       
Overigens is dit met de cykelnotatie nog veel efficiënter te schrijven als   (1)(2  3)(1 2 3) = (2)(1 3)
Bij een klein aantal elementen (zoals 3 in dit voorbeeld) kun je zo'n afbeelding ook nog visueler voorstellen door de drie elementen als hoekpunten van een gelijkzijdige driehoek te nemen:
       

       
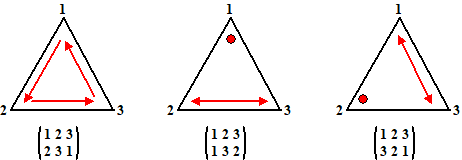
Het linkerplaatje is f(x) en is een rotatie tegen de klok in
Het middelste plaatje is g(x) en is een spiegeling in de hoogtelijn door hoekpunt 1.
Het laatste plaatje is  g(f(x)) en is een spiegeling in de hoogtelijn door hoekpunt 2.

Je ziet dat er zes mogelijke "bewerkingen" zijn, elk behorend bij een permutatie van de elementen {1, 2, 3}. En die bewerkingen na elkaar uitvoeren levert weer één van de andere bewerkingen op. Die "bewerkingen" (of permutaties) vormen een groep met zes elementen. Die groep heet de permutatiegroep met orde 6 (er zijn zes permutaties) en graad 3 (er zijn 3 objecten {1, 2, 3} waar de permutaties op worden uitgevoerd).

Hier zijn ze nog een keer alle zes:
       

       
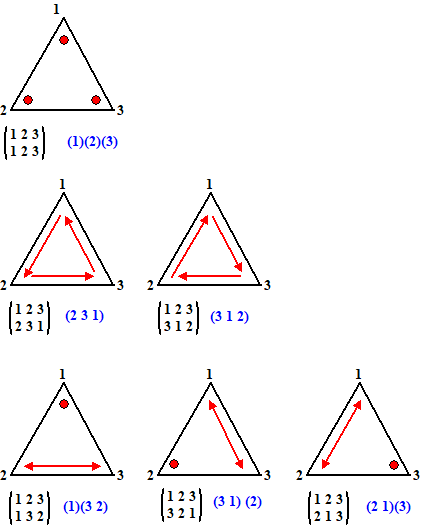
Daarbij staat in het blauw aangegeven hoe de notatie in cykels is. We onderscheiden drie gevallen. Eén geval van drie cykels (bovenaan), twee gevallen van één cykel (midden) en drie gevallen van 2 cykels (onderaan). Als we een cykel van orde k  noteren als  fk  en cykels achter elkaar aan als een product, dan hebben we dus  bovenaan  f13  , in het midden  2f3  en onderaan  3f1f2.
We definiëren nu de cykelindex van deze permutatiegroep als: 
       

       
Voor het NUT daarvan moet je even geduld hebben, dat komt nog.....
       
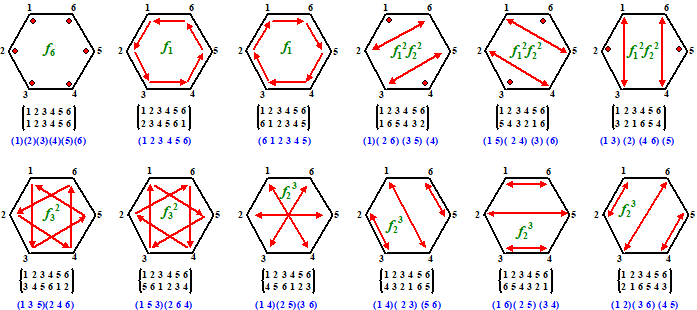
voorbeeld:  de cykelindex van de rotaties van een zeshoek.

Er zijn in totaal 12 mogelijke rotaties, immers je kunt één hoekpunt op zes plekken terecht laten komen, en je kunt elk geval van die zes gevallen ook de zeshoek nog "flippen". Dat wil zeggen optillen en andersom neerleggen.  Als we kijken waar de hoekpunten terechtkomen is de graad dus 6 (de hoekpunten), en de orde is 12.
Hieronder zie je ze alle twaalf, met de permutatienotatie (zwart)  en de cykelnotatie (blauw) eronder aangegeven. Bij de zes gevallen rechts is de zeshoek ook nog gespiegeld.
       

       
De cykelindex (groene f in de figuur) van deze groep is gelijk aan:
       
       
(merk nog even op dat de zes rotaties zonder spiegelen (links) ook apart nog een ondergroep vormen, en ook dat deze groep van 12 is op zich weer een ondergroep van alle 6! = 720 permutaties van een zeshoek)

Nogmaals:  het NUT van die cykelindex?  Nog even geduld.....
       
Een toepassing:  benzeenringen.
       
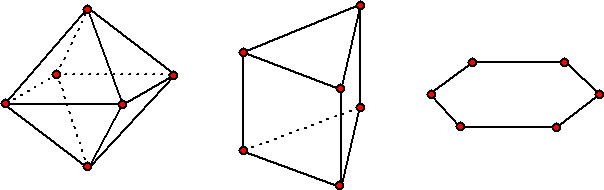
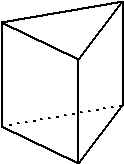
In de organische scheikunde bestaat er een structuur die heet  "benzeen", en die bestaat uit zes koolstofatomen en zes waterstofatomen (dus C6H6).  Nou kun je daar een boel nieuwe stoffen van maken door sommigen van die waterstofatomen te vervangen.
Als je twee H's vervangt krijg je een nieuwe stof met de formule  C6H4PQ.
Het blijkt, dat als je twee H's vervangt door P en Q, je zelfs DRIE nieuwe stoffen kunt krijgen, met dezelfde chemische formule, maar met verschillende eigenschappen. Dat heten isomeren van elkaar. Die verschillende eigenschappen kunnen dus niet komen doordat er verschillende atomen aanwezig zijn (want die zijn precies hetzelfde), maar moeten wel komen door het feit dat die atomen anders zijn gerangschikt. Het moest wel te maken hebben met de interne structuur van benzeen.

Op een gegeven moment waren er in de scheikundewereld drie modellen in omloop:  de C's van C6H6 zaten in een zeshoek, in een regelmatig achtvlak, of in een driehoekig prisma.
Zó dus:
       

       
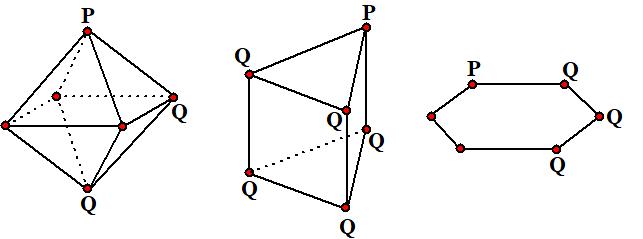
Hoe kunnen we beslissen welk van deze modellen de juiste is?
Laten we kijken naar het aantal manieren waarop we een P en een Q atoom aan C vast kunnen maken. Voor de plaats van een P zijn in de volgende figuren alle verschillende mogelijke Q-plaatsen aangegeven.
       

       
Bij het achtvlak zijn er twee plaatsen, bij het prisma 5, en bij de zeshoek 3.
Kijk goed uit bij dat prisma; het lijkt misschien alsof die bovenste twee Q's dezelfde figuur opleveren (net als die onderste twee), maar dat is niet zo! De figuren die je krijgt zijn spiegelbeelden van elkaar en niet dekkend te krijgen door te roteren! En spiegelbeelden hebben verschillende chemische eigenschappen.

Omdat in praktijk 3 isomeren van C6H4PQ werden gevonden was dat een sterke aanwijzing dat de C-moleculen van benzeen in een zeshoek geordend liggen.
Een sterke groepentheoretische aanwijzing!!!

Het algemene geval.
 
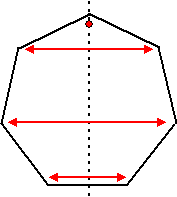
Stel dat we een permutatiegroep G hebben met graad n (dus n elementen die gepermuteerd worden). Dan noteren we de permutaties van een bepaalde soort op de cykel-manier van hierboven:

g1,3  is het aantal permutaties met één cykel van lengte 1 en drie van lengte 2. Je zult snappen dat deze groep dus graad 7 zal hebben (immers elk element komt één keer in elke cykel voor). De g's zijn de coëfficiënten van de fi in de cykel-index. g13 zou de coëfficiënt  van   f1f23  zijn. Bijvoorbeeld rotatie om de stippellijn hiernaast

Zo zou  g1,0,2,1 de coëfficiënt zijn van  het aantal permutaties van één cykel van lengte 1, nul van lengte 2, twee van lengte 3 en één van lengte 4. Dus bij een verzameling met 11 elementen.
In de cykelindex staat dan de term    g1,0,2,1 •  f1 f32f4

       
Oké nou eindelijk de toepassing van die mysterieuze cykel-index.
       
Stel dat we n knikkers hebben waarvan  r rood zijn,  b blauw  en g groen.  Op hoeveel manieren kunnen we die dan op de hoekpunten van een regelmatige n-hoek neerleggen?  (waarbij we twee ordeningen die door rotatie uit elkaar verkregen kunnen worden niet verschillend vinden).

Dan kun je dat in de volgende stappen berekenen:
• Schrijf de cykelindex van de permutatiegroep van de rotaties van de n-hoek op.
• Vervang nu elke fk daarin door  (xk + yk + zk)  waarbij x, y, en z staan voor een rode, blauwe en groene knikker

•

 Werk alle haakjes weg naar machten van x, y en z.

•

 De coëfficiënt van xrybzg  geeft nu het aantal manieren om de knikkers te ordenen.
       
voorbeeldje.
Leg de knikkers hiernaast (3 rood, 2 blauw, 1 groen)  op de hoekpunten van een zeshoek.
Op hoeveel verschillende manieren kan dat?

Eerst maar de cykelindex:

 
Die f2-en hielden we eerst nog apart maar mogen best samen (4f23).
Vul nu xk  + yk + zk in:
1/12 • { (x + y + z)6  + 2(x6 + y6 + z6) + 2(x3 + y3 + z3)2 + 4(x2 + y2 + z2)3 + 3(x + y + z)2(x2 + y2 + z2)2 }
We zoeken de coëfficiënt van x3y2z1  en daarvan vinden we alleen in de eerste term een stukje:
1/12(x3y2z • (6nCr 3)(3 nCr 2))  =  5x3y2z       (je ziet dat ik een multinomiaalcoëfficiënt heb gebruikt)

Kortom:  Er zijn vijf manieren.
       

       
       
Willekeurige permutaties.

Tot nu toe bekeken we steeds permutaties die rotaties voorstelden (om het midden of om één of andere as). We stappen nu naar de groep van ALLE permutaties. Dat wordt ook wel de Symmetriegroep Sn genoemd.
Wat is de cykelindex van zo'n Symmetriegroep  Sn ?

Daarvoor schrijven we een willekeurige permutatie eerst op een aparte manier op.  Een voorbeeld zal direct wel duidelijk zijn denk ik. Neem een verzameling van 9 elementen, waarvan we een willekeurige permutatie willen opschrijven. Dan tekenen we eerst de cykelvorm daarvan met blokjes, zó:
       

       
Hier staat een permutaties met cykels van lengte 1, 2, 2, 4 (we zetten ze van klein naar groot).
Om de permutatie compleet te maken vullen we deze blokjes vervolgens met een random volgorde van de getallen 1 tm 9.
Je ziet wel dat twee zulke verschillende volgorden best dezelfde permutatie kunnen opleveren. Bijvoorbeeld:
       

       
Eerste vraag die dan bij je opkomt:  "Op hoeveel manieren kan een gegeven permutatie met deze cykelvorm die hokjes vullen?"

•

 Als er i1 cykels van lengte 1 zijn, dan kunnen die op i1! in die enkele vakjes worden gezet.

•

 Als er i2 cykels van lengte 2 zijn, dan moeten die in de dubbele vakjes gezet worden, dat kan op i2! manieren,  maar daarna kun je ook nog de volgorde binnen elk vakje wisselen, dus in totaal  i2! • 2i2 manieren

•

 Als er i3 cykels van lengte 3 zijn, dan kunnen die op  i3! manieren in hun hokjes gezet worden, maar daarna kun je binnen zo'n hokje nog kiezen welk van de 3 volgorden je opschrijft; in totaal dus  i3! • 3i3
       
       
In ons voorbeeld hierboven zouden er dus  1 • 11 • 2! • 22 • 1 • 41 = 32 manieren om die ene permutatie P in de hokjes te zetten.  Maar omdat er in totaal  9! = 362880 permutaties mogelijk zijn, en elke van deze P's er 32 keer in voorkomt, zijn er dus  362880/32 = 11340 verschillende permutaties van de vorm g1,2,1
Dus in de cykelindex van de symmetriegroep met n = 9  zal de term  11340 • f1 • f22 • f4  staan.

Een paar kleine symmetriegroepen als voorbeeld.....
       
S3  (in totaal  3! = 6 permutaties)  
  cykelvorm 1 + 1 + 1  heeft  3! • 13 = 6 manieren per permutatie, dus in totaal  6/6 = 1 permutatie.
cykelvorm 1 + 2  heeft  1! • 11 • 1! • 21 = 2 manieren per permutatie, dus in totaal 6/2 = 3 permutaties
cykelvorm  3 heeft  1! • 31 = 3 manieren per permutatie, dus in totaal  6/3 = 2 permutaties.
De cykelindex van S3 is dus
 

  Herken je 'm nog? Het was die van rotaties van een gelijkzijdige driehoek.
       
S4  (in totaal 4! = 24 permutaties)
  cykelvorm 1 + 1 + 1 + 1  heeft  4! • 14 = 24 manieren per permutatie, dus in totaal 24/24 = 1 permutatie
cykelvorm  1 + 1 + 2  heeft  2! • 12 • 1! • 21 = 4 manieren per permutatie, dus in totaal 24/4 = 6 permutaties.
cykelvorm  1 + 3  heeft  1! • 11 • 1! • 31 = 3 manieren per permutatie, dus in totaal 24/3 = 8 permutaties.
cykelvorm  2 + 2  heeft  2! • 22 = 8 manieren per permutatie, dus in totaal 24/8 = 3 permutaties.
cykelvorm 4  heeft  1! • 41 = 4 manieren per permutatie, dus in totaal 24/4 = 6 permutaties.
De cykelindex van S4 is dus:
 
  Grappig:  het blijkt dat dit de groep is van de rotaties van de diagonalen van een kubus!
       
Een aardige toepassing van de cykelindex kun je nog vinden in deze les over aliphatische alcoholen.
       
           
  OPGAVEN
           
1. Toon met behulp van een cykelindex-berekening aan dat het aantal manieren om een P-atoom en een Q-atoom aan een (zeshoekige) benzeenring vast te maken  gelijk is aan 3.
           
2. Op hoeveel manieren kun je met drie kleuren verf de hoekpunten van een gelijkzijdige driehoek verven?
Denk erom dat er niet is gegeven hoeveel hoeken een bepaalde kleur moeten krijgen, dus je moet alle mogelijkheden bekijken!!
           
3. Geef de cykelindex van S5.
           
4. Geef de cykelindex van de rotaties van de hoekpunten van het prisma hiernaast. Met boven- en ondervlak een gelijkzijdige driehoek.

Denk erom dat het wel rotaties moeten zijn; spiegelingen die niet door rotaties verkregen kunnen worden tellen niet!

Controleer vervolgens dat er inderdaad met zulke rotaties 5 verschillende manieren zijn om een P en een Q en 4C's op de hoekpunten te plaatsen.

           
5. De rotaties die een kubus op zichzelf afbeelden vormen een groep. Deze rotaties permuteren de 8 hoekpunten, maar ook de 6 middens van de vlakken en ook de 4 lichaamsdiagonalen van de kubus.
Geef van elk van deze drie permutatiegroepen de cykelindex.
           
6. De cykelindex voor rotaties van de hoekpunten van een kubus is de volgende:
 
  (voor een uitleg daarvan:  zie het antwoord op de vorige vraag)
Bereken hiermee het aantal manieren om de hoekpunten van een kubus te kleuren met 1 rode, 2 groene en 5 blauwe hoekpunten.
       

7 manieren
       
       

© h.hofstede (h.hofstede@hogeland.nl)