partieel primitiveren


Partieel primitiveren.	© h.hofstede (h.hofstede@hogeland.nl)

Er is een slimme manier om de productregel van het differentiëren te gebruiken om functies te primitiveren.
Dit was de productregel: (f • g)' = f ' • g + f • g' .
Dat kun je ook zó schrijven: f ' • g = (f • g)' - f • g'

Dat lijkt nog steeds niet superspectaculair, maar het wordt wél interessant als je alles primitiveert:

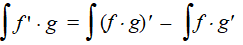Die eerste term aan de rechterkant is de primitieve van (f • g)' . Maar dat is natuurlijk f • g zélf, dus er staat:

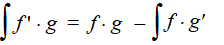Hier is een recept om van een productfunctie een primitieve te maken. Kijk maar wat er eigenlijk gebeurt:

In woorden: Als je de primitieve van een productfunctie wilt weten, dan kun je het volgende doen:
• primitiveer de eerste en schrijf de tweede over
• trek er een integraal af waarbij je die geprimitiveerde overschrijft en nu de tweede functie differentieert.

Waarschijnlijk is het regeltje het duidelijkst als je het zó opschrijft:

Dit heet partieel primitiveren.

Wat heb je hier in vredesnaam aan? Het wordt alleen maar ingewikkelder!

Nou, dat is niet altijd waar! Dat zit hem in die g' ........
Je hebt namelijk wel eens functies waarvan de afgeleide veel makkelijker is dan de functie zelf. Als je die dan voor g kiest, dan wordt de primitieve makkelijker!

Voorbeeld 1. Geef de primitieve van x • lnx
Daar staat een product van twee functies dus we proberen ons nieuwe regeltje uit.
Kijk even kritisch welke van de twee we als f nemen en welke als g.
Nou weet ik dat de afgeleide van lnx gelijk is aan ¹/_x en dat is een stuk makkelijker om mee te werken dan met lnx.
Daarom kies ik hier voor g = lnx (dan mag ik die straks lekker differentiëren) en dus is f = x
Toepassen van ons regeltje geeft dan:

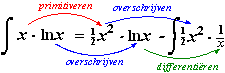En die laatste integraal is een makkie! Het is de primitieve van ¹/₂x en dat is ¹/₄x²
Daarmee wordt de totale primitieve van f(x) = xlnx gelijk aan F(x) = ¹/₂x²lnx - ¹/₄x² + c

Voorbeeld 2. Geef de primitieve van x • sinx
Deze keer is het net andersom: die sinx wordt helemaal niet simpeler als je hem differentieert, maar die x wél!
Kies daarom nu g = x en f = sinx.

Dat geeft: ∫sinx • xdx = -cosx • x - ∫ -cosx • 1dx

Dus de primitieve van f(x) = xsinx is gelijk aan F(x) = -xcosx + sinx + c

Leuk trucje...

Je kan dit partieel primitiveren zelfs gebruiken als er maar één functie staat!
Neem bijvoorbeeld de primitieve van lnx.
Als je dat leest als 1 • lnx dan kun je partieel primitiveren, met g = lnx en f = 1

Dat geeft ∫1 • lnx dx = xlnx - ∫ x • (1/x)dx = xlnx - ∫1dx = xlnx - x

Nog leuker trucje...

Stel dat je de primitieve zoekt van e^xsinx
Partieel primitiveren geeft: ∫e^x sinx dx = e^x sinx - ∫e^xcosx dx

Dat lijkt niet veel op te schieten, maar kijk wat voor leuks er gebeurt als je de laatste integraal helemaal rechts nóg een keer partieel primitiveert:
∫e^x sinx dx = e^x sinx - ∫e^xcosx dx = e^xsinx - (e^xcosx + ∫ e^xsinxdx)

Als je de oorspronkelijke opgave F noemt, dan staat die F daar aan rechterkant wéér!
Er staat eigenlijk F = e^x sinx - e^xcosx - F
Breng die F naar de andere kant en je krijgt 2F = e^xsinx - e^x cosx
Daaruit volgt simpel dat F = ¹/₂e^x(sinx - cosx)


1.	Geef de primitieven van de volgende functies:

	a.		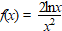d.	f(x) = ln(√x)

	b.	f(x) = x • ln²x	e.	f(x) x² • 2^x

	c.	f(x) = x • e^4x	f.	sinx • ln(cosx)

2.	Geef de primitieven van de volgende functies:

	a.	f(x) = x²cosx	c.	f(x) = x • cos(lnx)

	b.	f(x) = (2x² - 4x)e^2x	d.	f(x) = e^x• cos(3x)

3.	examenvraagstuk VWO, Wiskunde B, 1988. Met domein R⁺ is voor elke p ∈ R gegeven de functie f : x → ln²x+ 2lnx - 3 Bereken de oppervlakte van het vlakdeel ingesloten door de grafiek van f en de x-as.