|
|
 |
|
Oppervlakte. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
| Hieronder zie je een
aantal "basisoppervlakten" die je waarschijnlijk (hopelijk) al wel kent. |
| |
|
|
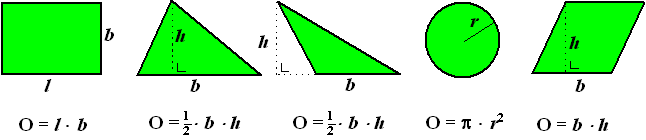 |
| |
|
| Merk nog even op dat de tweede en
derde figuur eigenlijk hetzelfde zijn! Je moet de hoogte van een
driehoek loodrecht op de basis kiezen, dus die kan soms buiten de
driehoek vallen, zoals in de derde figuur. Het wordt pas interessanter
als we verschillende figuren gaan combineren, of er delen van gaan
afsnijden.
Een paar voorbeelden zullen de verschillende tactieken om een
oppervlakte uit te rekenen wel duidelijk maken, denk ik. |
| |
|
|
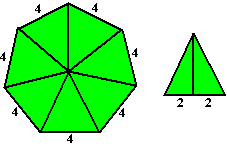
1. Een regelmatige veelhoek. |
| |
|
Als je de oppervlakte van een regelmatige
veelhoek moet uitrekenen kun je hem het best in driehoeken verdelen die
allemaal met de top in het middelpunt liggen en als basis een zijde
hebben. De regelmatige zevenhoek hiernaast wordt zo in 7 driehoeken
verdeeld.
De zeven hoeken bij het midden zijn dus elk 360/7
= 51,43º
Als je één zo'n driehoek bekijkt heeft hij dus een tophoek van 51,4º en
een basis van 4.
De halve tophoek is dan 25,7º dus voor de hoogte h geldt
tan(25,7º) = 2/h
Daaruit volgt h = 2/tan(25,7º)
≈ 4,15
en de oppervlakte van de driehoek is dan 1/2
• 4,15 • 4 = 8,31
De hele zevenhoek heeft dan oppervlakte 7 • 8,31
≈ 58,1. |
 |
| |
|
|
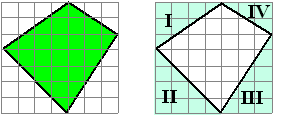
2. Inlijsten. |
| |
|
De oppervlakte van de groene vierhoek
hiernaast kun je makkelijk berekenen als je er een lijstje van vier
driehoeken omheen zet!
De totale oppervlakte van het vierkant is 7
× 7 = 49 en daar moeten vier driehoeken af.
Die hebben achtereenvolgens oppervlaktes 6, 8, 71/2
en 3
Dus de vierhoek heeft oppervlakte 49 - 6 - 8 - 71/2
- 3 = 241/2 |
 |
| |
|
|
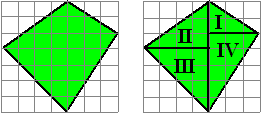
3. Onderverdelen. |
| |
|
Dezelfde vierhoek kun je ook berekenen door
hem in allemaal driehoeken te verdelen.
Hiernaast zie je dat de oppervlakte dan gelijk is aan:
3 + 6 + 8 + 71/2
= 241/2
|
 |
| |
|
| |
|
|
OPGAVEN |
| |
|
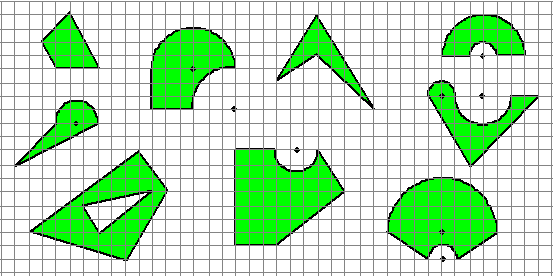
| 1. |
Bereken de oppervlakte van de volgende figuren.
De gekromde lijnen zijn allemaal delen van cirkels waarvan de
stippen het middelpunt aangeven. Alle hoekpunten zijn uiteraard
roosterpunten. |
| |
|
|
|
| |
 |
| |
|
|
|
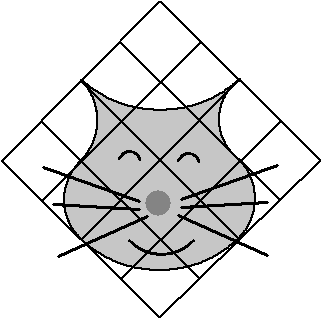
| 2. |
olympiadevraagstuk
De
omtrek van de kat hiernaast bestaat uit zes kwartcirkels.
Bereken de oppervlakte als de hokjes 1 bij 1 zijn.
Geef je antwoord exact (dus niet afronden) |
 |
| |
|
|
|
| |
|
| 3. |
Een regelmatige negenhoek heeft zijden van 4 cm.
Bereken de oppervlakte in twee decimalen nauwkeurig. |
| |
|
|
|
| |
|
|
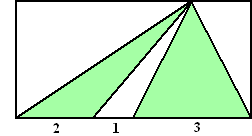
| 4. |
Hoeveel
procent van de oppervlakte van de rechthoek hiernaast is groen? |
 |
| |
|
|
| |
|
|
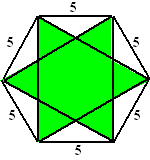
| 5. |
In een regelmatige
zeshoek met zijden van 5 wordt een ster getekend zoals in de
figuur hiernaast.
Bereken de oppervlakte van de ster in twee decimalen nauwkeurig.
Laat ook zien dat deze oppervlakte precies 2/3
deel van de zeshoek is. |
 |
| |
|
|
|
| |
|
|
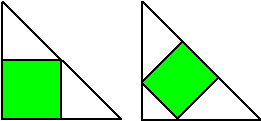
| 6. |
Hiernaast
staan twee manieren om een vierkant te tekenen in een gelijkbenige
rechthoekige driehoek.
Bereken de verhouding tussen die twee oppervlaktes |
 |
| |
|
|
|
| |
|
|
|
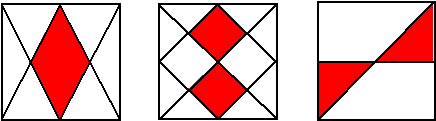
| 7. |
Hieronder
zijn in drie even grote vierkanten drie gebieden rood gemaakt.
Bereken de verhouding van de oppervlaktes van die gebieden. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
|
|
|
| 8. |
Bereken de
oppervlakte van de blauwe driehoek hiernaast |
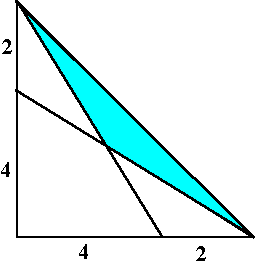 |
| |
|
|
| |
|
|
|
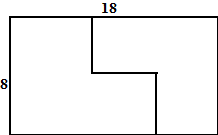
| 9. |
Een rechthoek van 18
bij 8 wordt zoals hiernaast in twee stukken gesneden. Dat wordt
zó gedaan dat je met die twee stukken een vierkant kunt leggen.
Bereken de lengte van de zijden van dat vierkant. |
 |
| |
|
|
|
| |
|
|
|
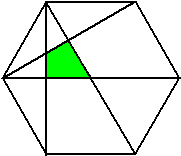
| 10. |
Hoeveel procent is de
gekleurde oppervlakte van de regelmatige zeshoek hiernaast? |
 |
| |
|
|
|
 |
|
| |
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
| |
|