oplossingsmatrix


De Oplossingsmatrix.	© h.hofstede (h.hofstede@hogeland.nl)

Even je geheugen opfrissen:

•

Een verbindingsmatrix (V) van een graaf was een matrix met enen en nullen die aangeeft of je van een knooppunt naar een ander knooppunt kunt gaan.

•

Als je V², V³, V⁴,... berekent geven die matrices het aantal manieren om in 2, 3, 4, ... stappen van een knooppunt naar een ander knooppunt te komen.

Je kunt die matrices natuurlijk ook optellen:

V + V² geeft het aantal manieren om in 1 óf 2 stappen van een knooppunt naar een ander knooppunt te gaan.
V + V² + V³ geeft het aantal manieren om in 1 óf 2 óf 3 stappen van een knooppunt naar een ander knooppunt te gaan.
....
V + V² + V³ + ... + Vⁿ geeft het aantal manieren om in hoogstens n stappen van een knooppunt naar een ander knooppunt te gaan.

Als je die V + V² + V³ + ... + Vⁿ gaat uitrekenen dan zou het kunnen dat je op een gegeven moment een matrix krijgt zonder nullen. Dat betekent dat bij die matrix vanuit elk punt van de graaf elk ander punt te bereiken is. De matrix waarbij dat voor het eerst gebeurt heet de oplossingsmatrix van de graaf.

Voorbeeld.

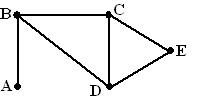
Bereken de oplossingsmatrix van de graaf hiernaast.

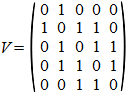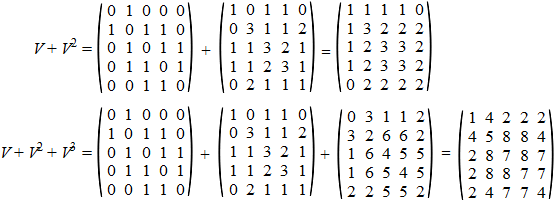En deze heeft geen nullen meer, dus dit is de oplossingsmatrix.

Bestaat zo'n oplossingsmatrix altijd?

Nou, alleen als elk punt van de graaf vanuit elk ander punt is te bereiken. Als dat niet zo is, zullen er altijd nullen in de matrices blijven staan. Een graaf met een oplossingsmatrix (als dus elk punt vanuit elk ander punt is te bereiken) heet samenhangend.

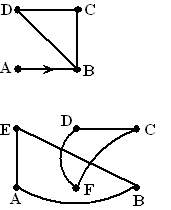
Hiernaast zie je twee mogelijkheden waarbij een graaf niet samenhangend is.
In de bovenste is punt A niet vanuit de andere punten te bereiken.
De onderste graaf bestaat eigenlijk uit twee "losse" delen (ABE en DCF)die geen verbinding hebben.

De diameter van een graaf.

De diameter van een graaf is de hoogste macht van V die nodig is om de oplossingsmatrix te verkrijgen. Het is dus het aantal benodigde stappen om elk punt vanuit elk ander punt te kunnen bereiken. Ofwel: het is de afstand tussen de twee punten van de graaf die het verst uit elkaar liggen.

OPGAVEN

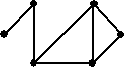
1.	Bereken de oplossingsmatrix en de diameter van de graaf hiernaast.

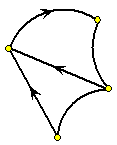
2.	Bereken de oplossingsmatrix en de diameter van de graaf hiernaast.

3.	Je kunt een kubus zien als een graaf. De hoekpunten van de kubus zijn dan knooppunten en de ribben zijn verbindingslijnen. Bereken de oplossingsmatrix en de diameter van een kubusgraaf.

4.	Hiernaast zie je de verbindingsmatrix V van een graaf. Leg uit hoe je zonder berekeningen te doen al kunt zien dat er geen oplossingsmatrix bestaat.

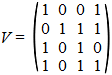5.	a.	Toon aan dat elke onsamenhangende graaf met n knooppunten ten hoogste ¹/₂ • (n - 1)(n - 2) verbindingslijnen heeft.

	b.	Het complement van een onsamenhangende graaf is samenhangend. Toon dat aan.

	c.	Als de graad van elk knooppunten van een graaf met n knoop[punten tenminste gelijk is aan ¹/₂ • (n - 1) dan is die graaf samenhangend. Toon dat aan.


© h.hofstede (h.hofstede@hogeland.nl)