© h.hofstede (h.hofstede@hogeland.nl)
   
1 Aan een groot voetbaltoernooi doen een heleboel buitenlandse ploegen mee.
Het is een knock-out toernooi, en dat betekent dat alleen de winnaars doorgaan naar de volgende ronde, wie verliest valt af en elke wedstrijd moet een winnaar en een verliezer opleveren (desnoods door strafschoppen).

Op een gegeven moment zijn er nog 8 teams over:  2 Engelse teams, 1 Nederlands team, 1 Frans team en maar liefst 4 Spaanse teams.
Er wordt geloot wie tegen wie moet spelen in de volgende ronde. Daarbij heeft elk team een even grote kans om tegen elk ander team te moeten spelen.

Hoe groot is de kans dat alle Spaanse teams tegen elkaar moeten spelen in de volgende ronde?
     

3/35
       
2. Een klein restaurant heeft een menukaart met daarop de keuze uit 8 voorgerechten, 6 hoofdgerechten en 10 nagerechten. Twee mensen bestellen onafhankelijk van elkaar een voorgerecht, een hoofdgerecht en een nagerecht.
Hoe groot is de kans dat zij precies twee dezelfde gerechten hebben besteld?
     

0,04375
       
3. Ik heb een schaaltje met 20 muntstukken. 12 daarvan zijn zuiver, en hebben een kans op kop 50% en munt ook 50%. De andere 8 zijn vals, en hebben een kans op kop 60% en munt 40%.
       
  a. Ik kies willekeurig een munt en gooi die op. Wat is de kans op KOP?
     

0,54
  b. Ik kies willekeurig twee munten en gooi die op. Wat is de kans op beiden MUNT?
     

0,2115
   
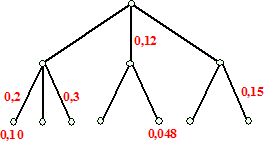
4. Hieronder zie je een kansboom, waarvan alle takken zijn getekend.
Van twee takken is de totale kans al uitgerekend. Die staat daar onderaan. Bereken de kansen op de andere takken.
       
 

       
5. Een muis heeft drie kamers om kaas in te zoeken.
Als de muis kamer 1 binnengaat zal hij de kaas na 3 minuten vinden.
Als de muis kamer 2 binnengaat zal hij 4 minuten zoeken en niets vinden. In dat geval verlaat hij de kamer.
Als de muis kamer 3 binnengaat zal hij 5 minuten zoeken en niets vinden. In dat geval verlaat hij de kamer.

Als de muis kamer 2 of 3 heeft verlaten kiest hij willekeurig een nieuwe kamer om binnen te gaan (het kan best wéér kamer 2 of 3 zijn).

Wat is de kans dat de muis in 12 minuten of minder de kaas vindt?
     

19/27
       
6. Vier personen A, B, C spelen met een zuivere dobbelsteen.
Als er 1 of 2 of 3 wordt gegooid, krijgt A een punt.
Als er 4 of 5 wordt gegooid, krijgt B een punt.
Als er 6 wordt gegooid, krijgt C een punt.
Degene die het eerst twee punten heeft is winnaar.
       
  a. Bereken de kans dat B in twee worpen wint.
     

1/9
  b. Bereken de kans dat C in precies drie worpen wint.
     

10/216
  c. Bereken de kans dat A in precies 4 worpen wint.
     

1/12
       
7. Een bezoeker aan een dancing heeft in zijn portemonnee 6 munten van 1 euro en 8 munten van 50 eurocent. Om naar binnen te mogen moet hij € 2,00 betalen.
Hij pakt aselect één voor één een munt uit zijn portemonnee en geeft deze aan de kassajuffrouw. Hij gaat door totdat hij voldoende geld uit zijn zak heeft gehaald om de disco binnen te kunnen (gepast hoeft dus niet).
       
  a. Bereken de kans dat hij meer dan 3 munten moet pakken.
     

2/13
  b. Bereken de kans dat hij gepast gaat betalen.  
     

0,6963
       
8. Het feit of het op een bepaalde dag regent of niet hangt af van hoe dat de vorige dag was.
De volgende kansen blijken te gelden:
Als het op een dag regent is de kans dat het de dag daarna wéér regent gelijk aan 0,57, dus de kans dat het die volgende dag droog is is 0,43.
Als het op een dag droog is, is de kans dat het de dag daarop wéér droog is gelijk aan 0,68, dus de kans dat het de volgende dag regent is dan 0,32.

Vandaag is het maandag, en regent het.
Hoe groot is de kans dat het precies twee van de drie komende dagen (dinsdag, woensdag, donderdag) óók regent?
     

0,2966
       
9. Een conciërge van een middelbare school heeft een sleutelbos met daaraan 10 verschillende sleutels.
En man is wat dement aan het worden en weet niet meer goed welke sleutel bij welk slot hoort.
Als hij een deur moet openmaken probeert hij gewoon één voor één de sleutels totdat hij de goede heeft. Hij is nog wél zo slim bij te houden welke sleutel hij al heeft geprobeerd, zodat hij niet twee keer dezelfde zal proberen.
       
  a. Hoe groot is de kans dat hij een deur bij de vierde sleutel open krijgt?
     

0,1
  b. De conciërge beweert dat het niet vaak zal voorkomen dat hij de deur pas bij de laatste sleutel zal open krijgen. Dat zou wel érg toevallig zijn! De kans dat het de vierde keer lukt zal zeker groter zijn!
Geef een wiskundig commentaar.
       
  Helaas; de man takelt steeds verder af, en is op een gegeven moment al zo ver dat hij niet meer bijhoudt welke sleutel hij al heeft geprobeerd. Elke keer kiest hij weer een willekeurige sleutel van zijn bos.
       
  c. Hoe groot is nu de kans dat hij een deur bij de vijfde poging open krijgt?
     

0,06561
     
10. examenvraagstuk HAVO wiskunde A, 1995.  
       
  Bij het examen voor vinoloog (wijnkenner) moeten de kandidaten wijnen herkennen door te proeven. Uit een artikel komt de volgende tekst.
       
    'De examenkandidaten hebben zich een jaar lang op deze proeverij voorbereid. Het zijn bijna allemaal vaklui: restauranteigenaars, wijnimporteurs, slijters.
De opdracht lijkt simpel: combineer de 12 op het papier genoemde wijnen met het juiste glas. Om de slagen wordt genoegen genomen met 9 juiste combinaties. Dat dit in de praktijk een hels karwei is blijkt wel uit het geringe aantal kandidaten dat succesvol is: gemiddelde zo'n 30 procent'.
       
  In deze opgave kijken we naar de kans dat iemand die helemaal geen verstand van wijnen heeft het examen haalt. Omdat hij uitsluitend gokt noemen we hem een gokker. Er staan volgens bovenstaande tekst 12 glazen met wijn op tafel. Iedere deelnemer krijgt 12 kaartjes met de namen van die wijnen. De opdracht is: leg bij elk glas het goede kaartje. De gokker legt zijn kaartjes dus in willekeurige volgorde bij de verschillende glazen.
       
  a. Op hoeveel verschillende manieren kan de gokker de kaartjes neerleggen?
       
  Om het iets gemakkelijker te maken heeft de examencommissie de 12 wijnen in 4 groepjes van 3 verdeeld. Bij elk groepje liggen 3 kaartjes met de namen van die drie wijnen. De opdracht aan de kandidaat is om bij elk groepje de kaartjes bij het juiste glas te leggen.
       
 

       
  Bij één groepje van drie wijnen en bijbehorende kaartjes kan voor de gokker de volgende kansentabel opgesteld worden:
       
 
aantal goed neergelegde kaartjes 0 1 2 3
kans op dat aantal 2/6 3/6 0 1/6
       
  b. Leg uit dat de kans op 2 goed neergelegde kaartjes 0 is, en dat de kans op 3 goed neergelegde kaartjes 1/6 is.
       
  c. Bereken de kans dat de gokker in deze situatie (4 groepjes van 3) alle 12 kaartjes goed neerlegt.
       
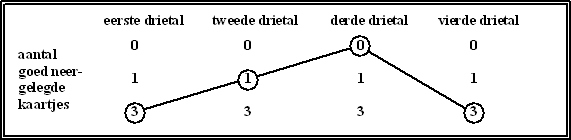
  In de volgende figuur is een mogelijk verloop van het examen in beeld gebracht. Het is de 'route' 3-1-0-3  met in totaal 7 goed geraden wijnen.
       
 

       
  Om te slagen moeten er minstens 9 wijnen goed geraden worden.
       
  d. Schrijf alle routes op met 9 of meer goed geraden wijnen.
       
  e. Bereken de kans dat een gokker slaagt.
       
11. examenvraagstuk HAVO Wiskunde A, 1997.
       
  Als een enquête over een gevoelig onderwerp gaat, zoals sex, misdaad of drugs, dan stuit de onderzoeker op problemen. Mensen zijn bij dit soort onderwerpen niet geneigd om zomaar alles over zichzelf te vertellen. Sommige mensen geven geen antwoord op dit soort vragen. Dit verschijnsel heet non-respons.
       
  a. Leg uit waarom een grote non-respons ongunstig is voor het onderzoek.
       
  Bij vragen over gevoelige onderwerpen komt het ook voor dat mensen geen eerlijk antwoord geven. Als de ondervraagden er van overtuigd zijn dat niet te achterhalen is hoe ze hebben geantwoord, zullen ze wel eerlijk willen antwoorden. Daartoe wordt gebruik gemaakt van een 'neutrale' vraag, bijvoorbeeld de vraag "Bent U in de maand april jarig?"  een deel van de ondervraagden beantwoordt de gevoelige vraag, anderen beantwoorden de 'neutrale' vraag. Alleen de ondervraagde zelf weet welke vraag hij heeft beantwoord.

De onderzoeker neemt aan dat de kans dat een willekeurige deelnemer aan de enquête in april jarig is, gelijk is aan 0,082
       
  b. Leg uit hoe de onderzoeker aan het getal 0,082 komt.
       
  Een enquête, waarbij men wil uitzoeken hoeveel procent van de bevolking wel eens zonder geldig kaartje reist, wordt nu als volgt opgezet.
Op een tafel staat een vaas met 15 rode en 35 blauwe ballen. Daarnaast liggen enquêteformulieren zoals hieronder afgebeeld.
       
 

       
  Zonder dat de onderzoeker het kan zien pakt de deelnemer aan deze enquête blindelings een bal uit de vaas. Daarna vult hij het formulier in en legt de getrokken bal terug.
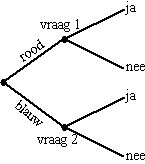
  Zo kan de onderzoeker onmogelijk weten of de ondervraagde vraag 1 of vraag 2 heft beantwoord. Toch kan de onderzoeker bepaalde conclusies uit de enquête trekken. In de figuur hiernaast is deze onderzoeksopzet schematisch weergegeven.

De enquête werd door 1257 mensen ingevuld. We nemen aan dat iedereen een eerlijk antwoord gaf.

Stel dat 9% van degenen die vraag 2 moesten beantwoorden "JA" heeft ingevuld. Van degenen die vraag 1 moesten beantwoorden heeft ook een aantal "JA" ingevuld.

       
  c. Hoeveel keer "JA" mag men in totaal bij deze enquête verwachten? Licht je antwoord toe.
       
  De onderzoeker weet uiteraard niet hoeveel procent van degenen die vraag 2 moesten beantwoorden "JA" heeft ingevuld. Anders was de enquête niet nodig geweest. Hij moet dit juist uit het totaal aantal keren "JA" afleiden.
Stel dat in totaal 75 keer "JA" werd geantwoord.
       
  d. Maak op grond van deze uitkomst een schatting van het percentage mensen dat "in de afgelopen drie maanden wel eens met opzet zonder geldig kaartje met het openbaar vervoer reisde". Licht je werkwijze toe.
       
12. Examenvraagstuk VWO Wiskunde A, 2006.

Schoenwinkel Boermans bestaat 40 jaar. Om dat te vieren overweegt eigenaar Boermans om een actie met kraskaarten te houden. Iedere klant die voor tenminste 50 euro in de winkel besteedt krijgt een kraskaart. Op elke kraskaart komen acht vakjes die open gekrast kunnen worden. In zes willekeurig gekozen vakjes staat het woord 'jammer!'. In de andere twee vakjes staat het gezicht van Boermans afgebeeld. De klant mag naar keuze twee vakjes openkrassen. Indien een klant tenminste éénmaal het gezicht van Boermans te voorschijn krast, dan levert dat de klant een cadeaubon op.

Een klant die een kraslot mag gaan krassen heeft een kans van 26/56 op een cadeaubon. 
       
  a. Laat met een berekening zien dat deze kans juist is.
       
  Het is mogelijk dat de vijfde klant die op een dag gaat krassen de eerste klant is die op die dag een cadeaubon wint.
       
  b. Bereken de kans dat dit gebeurt.
     

0,0382
  Boermans verwacht dat hij per dag gemiddeld 13 cadeaubonnen zal moeten uitdelen. Deze verwachting baseert hij op het gemiddelde aantal klanten per dag die in het verleden 50 euro of meer besteedden.
       
  c. Bereken dit gemiddelde aantal klanten per dag waarvan Boermans is uitgegaan.
     

28
       
13. De schatbewaarder van de koning heeft de opdracht gekregen om elk  van 100 kruiken te vullen met 100 goudstukken. De man is echter een bedrieger en vervangt in elke kruik één goudstuk door een muntstuk van nepgoud (zodat hij zelf met 100 goudstukken naar huis gaat). De koning vermoedt echter bedrog en gaat de zaak controleren. De koning wil kiezen uit twee controlemethoden:

•  Bij methode 1 neemt hij uit elke kruik één munt en kijkt of deze vals is.
•  Bij methode 2 neemt hij uit 25 kruiken elk 4 munten (in één greep) en kijkt of er valse bij zijn.

Bij beide methoden onderzoekt de koning dus 100 munten. Toch vraagt hij zich af of de twee methoden even goed zijn.

Bereken voor beide methodes de kans dat de schatbewaarder betrapt zal worden.
     

0,634
0,640
       
14. Vlaamse Olympiade.

In de laatste finaleweek van de quiz "De slimste mensaap ter wereld"  zijn nog zes apen in de running:  De mannetjes Choco en Chico en de wijfjes  Dipsie, Dixie, Dinky en Diggie.
Elke dag strijden drie apen tegen elkaar.
Op de eerste drie dagen valt er telkens één aap definitief af,  en de dag erna komt er een andere aap in de plaats.
Op donderdag wint één van de drie overblijvende apen de grote finale.
Op maandag starten Dipsie, Dixie en Choco.
Daarna komen Dinky (dinsdag), Chico (woensdag) en  Diggie (donderdag) er telkens bij als nieuwe kandidaat.
Als je weet dat de 6 apen allen even sterke quizzers zijn, hoe groot is dan de kans dat een mannetje de finale wint?
     

26/81
       
15. Vlaamse Olympiade.

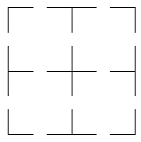
In de figuur zie je een gebouw met vier kamers.
Adrian staat binnen en gaat drie keer willekeurig door een deuropening.
Wat is de kans dat hij daarna opnieuw binnen staat?

     

5/8
16. Vlaamse Olympiade.

Kies een willekeurig getal x uit  [0, 5]  en een willekeurig getal y uit  [0,2]
Hoe groot is de kans dat x groter is dan y?
     

0,8
17. Een dobbelsteen is gemaakt door op een kubus zelfklevende stippen te plakken.
Helaas is één van deze stippen eraf gevallen.

Hoe groot is nu de kans om met deze dobbelsteen 5 te gooien?
     

11/63

© h.hofstede (h.hofstede@hogeland.nl)