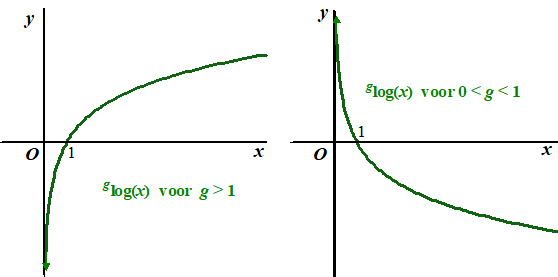© h.hofstede (h.hofstede@hogeland.nl)

 
Ongelijkheden.
       
In de les over de grafieken van glog(x) vonden we het volgende:
       
glog(x)  bestaat alleen voor x > 0 en de grafiek heeft bij x = 0 een asymptoot.
       
Dat betekent dat het Domein van de grafieken [0, →〉 is. Dat zijn namelijk de x-waarden die toegestaan zijn.
Die grafieken zagen er zó uit:
       

       
Je ziet dat ze beiden niet bestaan voor x ≤ 0.

Door allerlei transformaties  (we kennen er al 6) kun je die grafieken gaan veranderen. Je zou dan stap voor stap kunnen gaan bekijken hoe de grafiek verandert dus wat het nieuwe domein wordt en wat de nieuwe asymptoot wordt.

Maar het is handiger om alleen naar het eindresultaat te kijken en dan te bedenken dat wat daar onder de log staat groter dan nul moet zijn.
Dus:
       
glog(☺)  bestaat alleen voor ☺ > 0 en de grafiek heeft bij ☺ = 0 een asymptoot.
       
Die smiley mag nu elke formule met x-en zijn.
       
Voorbeeld 1.   Geef het domein de asymptoot van de grafiek van  y = 3 + 2log(5x + 25)

Oplossing.
Voor het domein hoef je alleen naar dat blokje (5x + 25) te kijken, die 3 doet er niet toe.
5x + 25  > 0
5x > -25
x > -5
Het domein is dus  [-5, →〉  en de verticale asymptoot is de lijn  x = -5
       
Voorbeeld 2.  Geef het domein en de asymptoot van de grafiek
van  y = 10 - 5log(x2 - 2x)

Oplossing.
Voor het domein hoef je alleen naar dat blokje (x2 - 2x) te kijken.
x2 - 2x  = 0
x(x - 2) = 0
x = 0  ∨  x = 2
x2 - 2x  is groter dan nul voor  kleiner dan 0  of  x groter dan 2
Het domein is dus   〈←, 0 〉 ∪  〈2, → 〉  en de verticale asymptoten zijn x = 0  en  x = 2.
(dat tekentje ∪ betekent  "samen met")

De grafiek ziet er trouwens ongeveer zó uit:
 
 
       
Gevolgen voor vergelijkingen
       
Soms vallen sommige oplossingen die je vindt toch af omdat ze niet in het domein zitten.
Kortom:  Je moet altijd je oplossingen controleren.

Kijk maar:
       
Voorbeeld 3.   Los op:    Los op:   2log(x2 - 5) = 2log(4x)

Oplossing:
x2 - 5= 4x
x2 - 4x - 5 = 0
(x - 5)( x + 1) = 0
x = 5  ∨  x = -1
Maar voor x = -1 bestaat  2log(x2 - 5)  helemaal niet!!!!  En 2log(4x) trouwens ook niet!!!!!
De enige oplossing is daarom x = 5.
       
Gevolgen voor ongelijkheden.
       
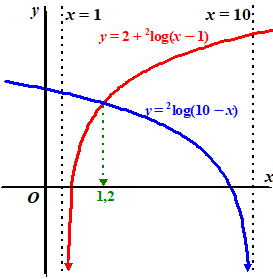
Dat domein van die log-grafieken heeft gevolgen voor het oplossen van ongelijkheden met log-formules erin. De basisaanpak voor het oplossen van ongelijkheden was meestal:

Als je moet oplossen  f  > g  dan doe je: 
•  Los eerst op  f = g
•  Kijk daarna in een plot van de grafieken voor welke waarden  f  boven g ligt.

Bij die laatste stap moet je je wel bedenken dat je alleen kunt zeggen dat een grafiek boven een andere ligt als ze wel beiden bestaan!!!!
Dat klinkt logisch natuurlijk, maar het heeft gevolgen voor het oplossen van ongelijkheden.
Kijk maar naar het volgende voorbeeld.
       
Voorbeeld 4.   Los algebraïsch op   2 + 2log(x - 1) ≥  2log(10 - x)

Oplossing:   Eerst berekenen we wanneer de beiden gelijk zijn:
 2 + 2log(x - 1) =  2log(10 - x)
2log(4) + 2log(x - 1) = 2log(10 - x)
2log(4x - 4) = 2log(10 - x)
4x - 4 = 10 - x
5x = 6
x = 1,2

In de figuur hiernaast zie je de schets van beide grafieken met het snijpunt aangegeven.

2 + 2log(x - 1) ≥  2log(10 - x)

Dus de rode grafiek moet boven de blauwe liggen.
Je ziet dat dat aan de rechterkant van 1,2 is.

Toch zou het fout zijn om nu simpelweg te zeggen  x ≥ 1,2.

Dat komt omdat die blauwe grafiek niet verder dan 10 gaat (het domein van de blauwe is  x < 10)

de correcte oplossing is daarom   [1.2,  10〉

(kijk nog even of je die beide haakjes goed begrijpt.... waarom is de ene recht en de ander geknikt?)
 
       
 
 
OPGAVEN
       
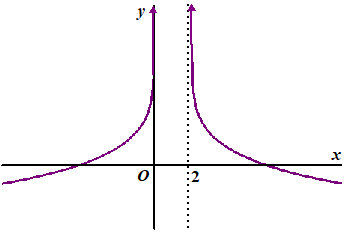
1. Geef van de volgende functies het domein en de vergelijking van de verticale asymptoot.
       
  a. f(x) = 2 + 5log(3x - 12)
       
  b. g(x) = 4 - 0,2log(x2 + 8x + 12)
       
2. Los de volgende ongelijkheden algebraïsch op:
       
  a. 5log(4x - 9)  ≤  2
       
  b. 4 + 2log(8 - x) ≤ 9
       
  c. 0,2log(4x - 12) - 6 > 0
       
3. Los de volgende ongelijkheden algebraïsch op:
       
  a. 3log(x - 8) ≥  3log(60 - 4x)
       
  b. 4log(x - 5) ≤  2 - 4logx
       
  c. 0,5log(3x + 15) ≤ 0,5log(x + 4) - 3
       
 

© h.hofstede (h.hofstede@hogeland.nl)