| 1. |
De Canon-Pixma-MP630 is een printer met 5 inktcartridges: één
grote voor zwarte inkt en 4 kleinere met de kleuren geel,
cyaan en magenta en weer zwart. Het aantal zwart-wit pagina's
tekst dat met de grote zwarte inktcartridge kan worden geprint
is normaal verdeeld met een gemiddelde van 800 en een
standaarddeviatie van 15. |
| |
|
|
|
|
| |
a. |
Met de laatste 5 cartridges die ik
kocht kon ik elke keer minder dan 790 pagina's tekst afdrukken.
Hoe groot is de kans dat zoiets gebeurt als de gegevens
hierboven kloppen? |
| |
|
|
|
|
| |
Met de kleinere kleurencartridges
kun je 600 pagina's kleurenafdrukken printen met een
standaarddeviatie van 15 pagina's. |
| |
|
|
|
|
| |
b. |
Als ik op een gegeven moment de
620ste kleurenafdruk wil maken, hoe groot is dan de kans dat
precies twee van de vier kleurencartridges het nog doen? |
| |
|
|
|
|
| |
|
|
2. |
De lengte van een partij
zonnebloemen is normaal verdeeld met een gemiddelde van 90 cm en
een standaarddeviatie van 9 cm. Als ik 30 zonnebloemen uit
deze partij krijg, hoe groot is dan de kans dat minstens 20 van
die bloemen een lengte tussen 85 en 100 cm hebben? |
| |
|
|
|
|
| |
|
|
3. |
De systolische bloeddruk (bovendruk)
bij volwassenen is normaal verdeeld met een gemiddelde van 117
en een standaarddeviatie van 18. Een arts meet op een dag
van 20 mensen de bloeddruk. Hoe groot is de kans dat: |
| |
|
|
|
|
| |
a. |
bij hoogstens 4 mensen de bloeddruk
hoger is dan 125? |
| |
|
|
| |
b. |
meer dan 8 mensen een bloeddruk
tussen 110 en 120 hebben? |
| |
|
|
| |
c. |
precies 10 mensen een bloeddruk
hebben die niet meer dan 6 van het gemiddelde afwijkt? |
| |
|
|
|
|
| |
|
|
|
|
| 4. |
Een appelmoesfabrikant
laat zijn potten met biologische appelmoes vullen door een
vulmachine. Op de potten staat dat er 340 gram appelmoes inzit.
De vulmachine is echter niet zo nauwkeurig: het vulgewicht heeft
een standaarddeviatie van maar liefst 12 gram. Om geen boze
klanten te krijgen stelt de fabrikant de machine daarom af op
een gewicht dat hoger is dan 340 gram.
|
 |
| |
a. |
Op welk gewicht moet de machine
worden afgesteld zodat hoogstens 2% van de potten te weinig
appelmoes bevatten? |
| |
|
|
|
| |
Omdat de machine gemiddeld meer dan
340 gram in een pot moet doen gaat de fabrikant op zoek naar een
nauwkeuriger machine. De appelmoespottenvulmachinehandelaar
heeft 3 modellen in zijn assortiment, waarvan de prijs en
standaarddeviatie zijn zoals in de volgende tabel. Daarin staat
ook de verwachte levensduur van de machine (in aantal te vullen
potten) |
| |
|
|
|
|
| |
| model |
Astepo |
Galdi |
Fimer |
| standaarddeviatie (gram) |
10 |
8 |
6 |
| aantal potten (duizenden) |
300 |
250 |
320 |
| prijs (duizenden euro) |
120 |
100 |
140 |
|
| |
|
|
|
|
| |
De kostprijs van de appelmoes is
voor de fabrikant gelijk aan €0,40
per 100 gram. De machine die gekocht gaat worden moet zó worden
afgesteld dat weer hoogstens 2% van de klanten te weinig
appelmoes krijgt. |
| |
|
|
|
|
| |
b. |
Welk van bovenstaande drie modellen
kan de fabrikant het best aanschaffen? |
| |
|
|
|
|
| 5. |
De Olympische limiet om mee te mogen
doen aan het verspringen voor dames is 6.60 meter. Een atlete
weet dat haar sprongen normaal verdeeld zijn met een gemiddelde
van 6.40 meter en een standaarddeviatie van 13 cm. Om
uitgezonden te worden moet de atlete binnen een periode van een
half jaar minstens vijf keer voldoen aan deze limiet. In dat
halve jaar zijn er vier wedstrijden met elk 5 sprongen.
|
| |
|
|
|
|
| |
a. |
Bereken de kans dat de atlete zich
bij deze wedstrijden zal plaatsen voor de Spelen. |
| |
|
|
| |
b. |
Hoe hoog zou de Olympische limiet
moeten zijn om ervoor te zorgen dat haar plaatsingskans in dit
halve jaar minstens 90% is? |
| |
|
|
|
|
| |
c. |
Bereken de kans dat haar verste
sprong in dit halve jaar minstens 6.62 meter zal zijn. |
| |
|
|
|
|
| |
|
| 6. |
Voor het slotbal van
een Amerikaanse Highschool worden alle 30 de meisjes willekeurig
gekoppeld aan één van de 30 jongens. De lengte van de meisjes is
normaal verdeeld met een gemiddelde van 165 cm en een
standaarddeviatie van 10 cm. De lengte van de jongens is
ook normaal verdeeld met een gemiddelde van 178 cm en een
standaarddeviatie van 8 cm.
Een koppel op de dansvloer noemen we "vreemd" als het
meisje langer is dan de jongen.
Hoe groot is de kans op minstens 5 "vreemde" koppels? |
| |
|
|
|
|
| |
|
|
|
|
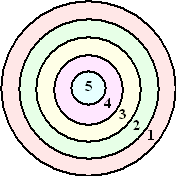
| 7. |
Een vereenvoudigd
DARTS-bord bestaat uit 5 cirkels met hetzelfde middelpunt en
stralen 3, 6, 9, 12, en 15 cm. Daardoor ontstaan vijf gebieden
die vanaf het midden respectievelijk 5, 4, 3, 2 en 1 punt
opleveren. Francien meet een groot aantal keren hoe ver haar
pijltje van het midden af komt, en die afstand blijkt normaal
verdeeld met een gemiddelde van 6 cm en een standaarddeviatie
van 3 cm. |
 |
| |
|
|
|
| |
a. |
Hoe groot is de kans dat zij bij één
keer gooien minimaal 3 punten scoort? |
| |
|
|
|
| |
b. |
Geef een kansverdeling van het
aantal punten bij één keer gooien en bereken daarvan de
verwachtingswaarde en de standaarddeviatie. |
| |
|
|
|
|
| 8. |
Een inkoper moet voor
zijn sportwinkel voor het hele zomerseizoen zwembroeken inkopen.
Hij verwacht er 1000 te verkopen, maar zeker weet hij dat niet.
Eigenlijk denkt hij dat het aantal verkochte zwembroeken de komende zomer
normaal verdeeld zal zijn met een gemiddelde van 1000 en een
standaarddeviatie van 60.
De inkoopsprijs is 20 euro, de verkoopsprijs 35 euro.
Aan het eind van het seizoen doet hij het overschot in de uitverkoop, en
zal die dan voor 15 euro verkopen.
Hij vraagt zich af hoeveel polo's hij moet inkopen om een zo
groot mogelijk winst te maken......... |
| |
|
|
|
|
| |
a. |
Stel dat hij overweegt een extra
zwembroek te kopen, en dat de kans p is dat hij die
inderdaad verkoopt.
Toon aan dat de verwachtingswaarde van de winst dan positief is
als p > 0,25. |
| |
|
|
|
|
| |
Als de verkoopkans van de nde
zwembroek gelijk is aan 0,25, dan is dat het grensgeval
van hoeveel zwembroeken de inkoper moet inkopen. |
| |
|
|
|
|
| |
b. |
Bereken voor de hoeveelste zwembroek
dat zo is, en los daarmee het probleem van de inkoper op. |
| |
|
|
|
|
| |
|
|
|
|
| 9. |
Een kogelstoter heeft in een zware
trainingsweek een groot aantal worpen gedaan.
De geworpen afstanden staan in de volgende tabel: |
| |
|
|
|
|
| |
| afstand (in m) |
aantal |
15,25 - < 16,75
16,75 - < 17,75
17,75 - < 18,25
18,25 - < 18,75
18,75 - < 19,75
19,75 - < 20,75 |
13
48
39
37
50
13 |
|
| |
|
|
|
|
| |
a. |
Laat m.b.v.
normaal-waarschijnlijkheidspapier zien dat deze verdeling bij
benadering een normale verdeling is. Bepaal het gemiddelde en de
standaarddeviatie. |
| |
|
|
|
|
| |
Neem voor de rest van deze opgave
aan dat μ = 18,25 en
σ = 1 |
| |
|
|
|
|
| |
b. |
Deze kogelstoter gaat meedoen in een
wedstrijd waarbij de resultaten van drie pogingen worden
opgeteld.
Bereken de kans dat hij in totaal meer dan 58 meter zal stoten. |
| |
|
|
|
|
| |
c. |
Deze kogelstoter gaat 30 worpen
doen.
Bereken de kans dat de beste worp meer is dan 19,1 meter? |
| |
|
|
|
|
| 10. |
examenvraagstuk VWO wiskunde A,
1984 Een machine spoelt garen op een klosje.
De lengte van de draad op een klosje is in praktijk normaal verdeeld
met een gemiddelde van 100 m en een standaardafwijking van 47 cm.
Aan het eind van de dag wordt een klosje aselect getrokken uit de
geproduceerde hoeveelheid en de lengte van de draad op dat klosje
wordt nauwkeurig gemeten.
Bij een afwijking van meer dan 60 cm van de voorgeschreven 100m,
wordt de machine opnieuw afgesteld. |
| |
|
|
|
|
| |
a. |
Laat zien dat
de kans dat de machine, ondanks een correcte instelling, toch
opnieuw wordt afgesteld, bij benadering 20% is. |
| |
|
|
|
|
| |
b. |
Neem aan dat de
machine gedurende een periode van drie weken (15 werkdagen) steeds
correct is ingesteld. Hoe groot is de kans dat in die periode
desondanks meer dan drie keer opnieuw wordt afgesteld? |
| |
|
|
|
|
| |
c. |
Er wordt een nieuwe
machine aangeschaft, die volgens de leverancier aanmerkelijk
nauwkeuriger werkt.
Men handhaaft de oude procedure waarbij dagelijks de draad van
een aselect gekozen klosje wordt nagemeten en een afwijking van
meer dan 60 cm tot gevolg heeft dat de machine opnieuw wordt
afgesteld.
Neem aan dat de lengte van de draad op een klosje ook voor de nieuwe
machine normaal verdeeld is. De kans dat die machine ten onrechte
opnieuw wordt afgesteld is bij benadering 10%.
Hoe groot is de standaardafwijking van de lengte van de draad op een
klosje? |
| |
|
|
|
|
|
11. |
examenvraagstuk HAVO wiskunde B,
2002. Een zwangerschap duurt
gemiddeld 40 weken.
Neem bij de volgende vragen aan dat de zwangerschapsduur normaal
verdeeld is. 85% van de zwangere vrouwen bevalt tussen de 266e
en de 294e dag. Uit deze gegevens is af te leiden dat de
standaardafwijking op gehelen afgerond 10 dagen is. |
| |
|
|
|
|
| |
a. |
Bereken de standaardafwijking
in één decimaal nauwkeurig. |
| |
|
|
|
|
| |
Neem in het vervolg van deze
opgave voor de standaardafwijking 10 dagen.
Baby's die geboren worden na een zwangerschap van 37 weken of minder
heten te vroeg geboren.
Volgens het Centraal Bureau
voor de Statistiek worden op een doorsnee dag in ons land 520
kinderen geboren. |
| |
|
|
|
|
| |
b. |
Bereken in gehele procenten de
kans dat er op een doorsnee dag tussen de 5 en 15 baby's te vroeg
geboren worden. |
| |
|
|
|
|
| |
|
|
|
|
|
12. |
examenvraagstuk HAVO wiskunde B,
2003.
Een boomkweker koopt een grote partij jonge
sparrenboompjes. Uit onderzoek is bekend dat de lengte van jonge
sparrenboompjes bij benadering normaal verdeeld is met een gemiddelde
van 25 cm en dat 5% van de boompjes korter is dan 20 cm. De partij jonge
sparrenboompjes is te beschouwen als een aselecte steekproef. |
| |
|
|
|
|
| |
a. |
Bereken de standaardafwijking
van de lengteverdeling van jonge sparrenboompjes. Geef je antwoord in
twee decimalen nauwkeurig. |
| |
|
|
|
|
| |
De kweker neemt steeds aselect
40 boompjes en plant deze in één rij. |
| |
|
|
|
|
| |
b. |
Bereken de kans dat in zo'n
rij precies één boompje korter is dan 20 cm. Rond je antwoord af op
twee decimalen. |
| |
|
|
|
|
| |
Na een aantal jaren wordt een
groot aantal van deze sparrenboompjes voor de kerstverkoop gerooid. Je
kunt er nu van uitgaan dat de lengte van deze partij bomen bij
benadering normaal verdeeld is met een gemiddelde van 145 cm en een
standaardafwijking van 15 cm. |
| |
|
|
|
|
| |
c. |
Bereken de kans dat een
aselect gekozen boom uit deze partij een lengte heeft die ligt tussen de
140 en de 170 cm. Rond je antwoord af op twee decimalen. |
| |
|
|
|
|
| |
De bomen worden ingedeeld in
twee prijsklassen, namelijk: kleine bomen van € 10,- per stuk en
grote bomen van € 15,- per stuk. De kweker wil dat de te verwachten
opbrengst per 100 bomen € 1300,- is. |
| |
|
|
|
|
| |
d. |
Bereken bij welke lengte de
grens tussen de beide prijsklassen dan moet liggen. Rond je antwoord af
op hele centimeters. |
| |
|
|
|
|
| |
|
|
|
|
|
13. |
examenvraagstuk HAVO wiskunde B,
2008. In een
café wordt bier getapt in glazen met een inhoud van 25 cl. Het is de
bedoeling dat er 20 cl bier (het vloeibare gedeelte) en 5
cl schuim in een glas komt. De hoeveelheid bier in
een dergelijk bierglas in dit café is bij benadering normaal
verdeeld. Alle leden van het barpersoneel tappen
gemiddeld 20 cl bier in een glas met een standaardafwijking
van 0,6 cl.
In dit
café is de kwaliteitsnorm: de hoeveelheid bier in een bierglas moet
liggen tussen 19 en 21 cl. |
| |
|
|
|
|
| |
a. |
Bereken hoeveel
procent van de glazen die het barpersoneel tapt, voldoet aan de
kwaliteitsnorm. |
| |
|
|
|
|
| |
b. |
Bereken de
kans dat van de tien glazen bier die het barpersoneel tapt er hoogstens
drie zijn met minder dan 19,5 cl bier. |
| |
|
|
|
|
| |
Regelmatig wordt er in het café 1 meter bier besteld.
Dat zijn 13 glazen bier op
een
rijtje. We bekijken nu de totale hoeveelheid bier van de 13 glazen die het
barpersoneel getapt heeft.
Ook de totale hoeveelheid bier is bij benadering normaal verdeeld, met een
gemiddelde van 260 cl. De kans dat de totale
hoeveelheid bier kleiner is dan
258
cl is 18%. |
| |
|
|
|
|
| |
c. |
Bereken de
standaardafwijking van de totale hoeveelheid bier. |
| |
|
|
|
|
| |
|
|
|
|
|
14. |
examenvraagstuk VWO wiskunde
A,
2007. Van een
groot aantal mensen in 25 verschillende beroepsgroepen is het IQ gemeten.
Voor elke beroepsgroep is vervolgens het gemiddelde IQ en
de standaardafwijking bepaald.
We nemen
aan dat binnen elke beroepsgroep het IQ van een
persoon uit die beroepsgroep normaal verdeeld is.
Het blijkt dat naarmate het
gemiddelde IQ van een beroepsgroep groter is, de
standaardafwijking kleiner is. Het volgende verband
geldt: σ = 45,5
– 0,272 • μ.
Hierin is σ
de standaardafwijking en μ
het gemiddelde IQ van
een beroepsgroep.
Uitgaande
van de normale verdeling kunnen we met deze formule voor elke waarde
van het gemiddelde m
berekenen hoe groot de kans is dat een persoon uit
een beroepsgroep met dat gemiddelde een IQ heeft dat
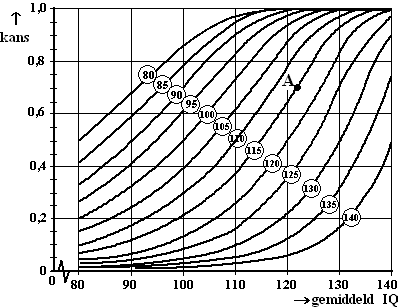
groter is dan 80, 85, 90, …, 135, 140. Het
resultaat van deze berekeningen is grafisch weergegeven
in
de volgende figuur:. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
Bij punt A
lezen we af dat de kans ongeveer 0,7 is dat een persoon uit een beroepsgroep
met gemiddeld IQ van 122 een IQ heeft
dat groter is dan 115. Ofwel in formulevorm:
P(IQ > 115) ≈ 0,7, waarbij μ
= 122. Uitgaande van het verband σ
= 45,5 – 0,272 • μ
kunnen we deze kans nauwkeuriger
berekenen. |
| |
|
|
|
|
| |
a. |
Bereken
deze kans. Geef je antwoord in 3 decimalen nauwkeurig. |
| |
|
|
|
|
| |
Uit een
grote beroepsgroep met een gemiddeld IQ van 110
worden willekeurig vier personen geselecteerd. We
willen de kans weten dat alle vier personen een IQ hebben
dat groter is dan 120. Deze kans kun je berekenen als je de kans weet
dat één willekeurig persoon uit deze beroepsgroep een IQ groter
dan 120 heeft. Deze laatste kans kun je
aflezen uit de figuur hierboven. |
| |
|
|
|
|
| |
b. |
Bereken op
bovenstaande wijze de kans dat alle vier personen een IQ hebben
groter dan 120. |
| |
|
|
|
|
| |
Een
vuistregel van de normale verdeling zegt dat 68% van de gegevens ligt
tussen de waarde μ
– σ
en de waarde μ
+ σ.
Deze vuistregel zou ook in de figuur hierboven terug
te vinden moeten zijn. |
| |
|
|
|
|
| |
c. |
Laat zien
dat deze vuistregel is terug te vinden in de grafieken van de figuur
hierboven Doe dit voor personen uit een
beroepsgroep met een gemiddeld IQ van 120.
Licht je werkwijze toe. |
| |
|
|
|
|
|
15. |
Examenvraagstuk VWO,
Wiskunde B, 2004. Een huisarts heeft op elke werkdag twee uren
gereserveerd voor een spreekuur. De ervaring heeft haar geleerd dat zij
tijdens het spreekuur gemiddeld tien minuten voor een patiënt nodig
heeft.
De huisarts deelt de patiënten die van haar spreekuur gebruik maken in
drie groepen in: |
| |
|
- gemakkelijke patiënten die hoogstens 5 minuten tijd
kosten.
- gewone patiënten die tussen de 5 en 15 minuten tijd
kosten
- tijdrovende patiënten die minstens 15 minuten tijd
kosten.
|
| |
We maken bij deze situatie het volgende
wiskundige model: |
| |
|
- elke werkdag komen er 12 patiënten op het spreekuur.
- De tijd die de huisarts tijdens het spreekuur voor een patiënt
nodig heeft is normaal verdeeld met een gemiddelde van 10 minuten en
een standaardafwijking van 4 minuten.
|
| |
|
|
|
|
| |
a. |
Bereken de verwachtingswaarde
van het aantal tijdrovende patiënten tijdens een spreekuur in twee
decimalen nauwkeurig. |
| |
|
|
|
|
| |
b. |
Bereken in twee decimalen
nauwkeurig de kans dat de huisarts tijdens een spreekuur 2 gemakkelijke
en 10 gewone patiënten krijgt. |
| |
|
|
|
|
| |
c. |
Bereken in twee decimalen
nauwkeurig de kans dat tijdens een spreekuur minstens zes patiënten meer
dan 10 minuten kosten. |
| |
|
|
|
|
| |
|
|
|
|
|
16. |
Een hovenier bij de
gemeentewerken plant op een gegeven moment 2000 nieuwe plantjes
in de stad. Hij weet dat de levensduur daarvan normaal verdeeld
is met een gemiddelde van 80 dagen en een standaarddeviatie van
20 dagen.
Na 50 dagen gaat hij alle plantjes controleren en vervangt
degenen die dood zijn door nieuwe plantjes (ook weer met
dezelfde gemiddelde levensduur en dezelfde standaarddeviatie
daarvan) |
| |
|
|
|
|
| |
a. |
Hoeveel plantjes moet hij vervangen? |
| |
|
|
|
|
| |
Nog eens 40 dagen later
vervangt hij wéér alle dode plantjes. |
| |
|
|
|
|
| |
b. |
Hoeveel plantjes moet hij deze keer
vervangen? |
| |
|
|
|
|
| |
|
|
|
|
|
17. |
Eieren worden wel in drie gewichtsklassen ingedeeld, namelijk
Small (S), Medium (M) en Large(L)
Medium eieren wegen 53-63 gram, Small eieren wegen minder en
Large meer.
Een boer heeft kippen waarvan hij weet dat die eieren leggen
waarvan het gewicht normaal verdeeld is met een gemiddelde van
60 gram en een standaarddeviatie van 8 gram.
Hij heeft een grote schaal met daarin 48 eieren van zijn
kippen. |
 |
| |
|
|
|
| |
a. |
Neem aan dat de verdeling S-M-L precies is zoals je volgens de
normale verdeling zou verwachten.
Als hij dan een doosje met 10 eieren uit zijn schaal vult, hoe
groot is dan de kans dat dat 6 Small, 3 Medium en 1 Large ei
zijn? |
| |
|
|
| |
b. |
S
en M eieren leveren hem €0,06 op en L-eieren leveren hem €0,08
op.
Hoe groot is de kans dat de 48 eieren uit de schaal minstens
€3,50 opleveren? |
| |
|
|
|
|
| |
|
|
|
|
|
18. |
Voor consumptie van Zeeuwse
mosselen onderscheidt men vijf gewichtsklassen, aflopend van
groot naar klein zijn dat: Goudmerk, Jumbo, Imperial, Super en
Extra |
 |
| |
|
|
|
| |
|
soort |
aantal stuks per kg |
prijs per mossel |
Extra
Super
Imperial
Jumbo
Goudmerk |
70 -
80
60 - 70
50 - 60
40 - 50
30 - 40 |
€
0,07
€ 0,08
€ 0,10
€ 0,12
€ 0,15 |
|
| |
|
|
|
|
| |
a. |
Laat
zien dat deze tabel in alle gevallen ongeveer dezelfde prijs per
kg mosselen oplevert |
| |
|
|
|
|
| |
Een mosselkweker weet dat het
gemiddelde gewicht van zijn mosselen normaal verdeeld is met een
standaarddeviatie van 10 gram.
Hij verwacht een voorraad van 20000 mosselen te kunnen verkopen
voor €800. |
| |
|
|
|
|
| |
b. |
Van
welk gemiddelde gewicht gaat hij uit? |
| |
|
|
|
|
|
19. |
Examenvraagstuk HAVO wiskunde A,
2016-I |
| |
|
|
|
|
| |
Tegenwoordig zijn bureaustoelen in
hoogte verstelbaar. Daardoor kunnen de meeste mensen de stoel
instellen op de zithoogte die voor hen ideaal is. De ideale
zithoogte van volwassen Nederlanders is normaal verdeeld met een
gemiddelde van 46,0 cm en een standaardafwijking van 3,8 cm.
Ontwerpers gebruiken deze gegevens om de ideale bureaustoel te
ontwerpen. Een ontwerper wil een bureaustoel maken
waarvan de hoogte instelbaar is door middel van een gasveer van 8,0
cm. Zie de figuur. De zithoogte kan dus 8,0 cm variëren. De
ontwerper moet nog wel kiezen tussen welke
minimumhoogte en maximumhoogte de zithoogte kan variëren, als er
maar 8,0 cm verschil tussen zit. In de tabel zie je twee mogelijke
situaties.
Er zijn veel meer mogelijkheden. |
 |
| |
|
|
|
|
| |
minimum-
hoogte |
maximum-
hoogte |
percentage van de
mensen dat
stoel op ideale hoogte kan
instellen |
| 44,0 cm |
52,0 cm |
64 (%) |
| 47,0 cm |
56,0 cm |
39(%) |
|
| |
|
|
|
|
| |
a. |
Toon
aan dat het onmogelijk is om met de gasveer van 8,0 cm de
stoel zó te maken dat meer dan 71% van de mensen de stoel op zijn
ideale zithoogte kan instellen. |
| |
|
|
|
|
| |
Er bestaan ook gasveren die langer zijn dan 8,0 cm.
Als de ontwerper een langere gasveer gebruikt, kunnen meer mensen de
bureaustoel op hun ideale zithoogte instellen.
De ontwerper zorgt ervoor dat de minimumhoogte en de
maximumhoogte even ver van 46,0 cm af liggen. Hij wil weten hoe lang
de gasveer dan moet zijn om ervoor te zorgen dat 90% van de mensen
de bureaustoel op zijn ideale zithoogte kan instellen. |
| |
|
|
|
|
| |
b. |
Bereken hoe lang de gasveer moet zijn. Geef het
antwoord in cm, afgerond op 1 decimaal. |
| |
|
|
|
|
| |
Een lange gasveer is erg duur. De ontwerper kiest er
daarom voor om een gasveer van 8,0 cm te blijven gebruiken. Hij
besluit om drie varianten te maken: |
| |
- |
een lage variant,
waarbij de zithoogte van 34,0 cm tot 42,0 cm kan worden ingesteld; |
| |
- |
een middelhoge variant,
waarbij de zithoogte van 42,0 cm tot 50,0 cm kan worden ingesteld; |
| |
- |
een hoge variant,
waarbij de zithoogte van 50,0 cm tot 58,0 cm kan worden ingesteld. |
| |
|
|
|
|
| |
c. |
De ontwerper beweert dat er zo voor meer dan 99% van
de mensen een stoel met hun ideale zithoogte is. Onderzoek of hij
gelijk heeft. |
| |
|
|
|
|
|
20. |
Het gewicht van een aantal mensen
is normaal verdeeld met een gemiddelde van 70 kg.
De kans dat er van de 20 mensen minstens 8 zwaarder zijn dan 80
kg is 12%
Welke gewichten hebben de lichtste 10% van deze mensen? |
| |
|
|
|
|
|
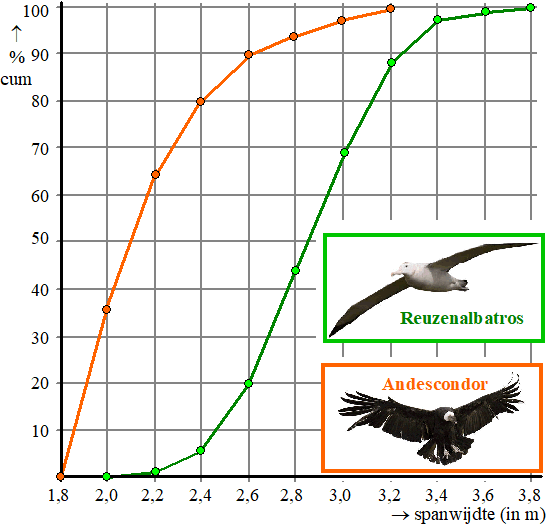
21. |
Biologen hebben de vleugelspanwijdte van een aantal volwassen
exemplaren van de Reuzenalbatros en de Andescondor en de
Zeearend gemeten. Zij maakten met hun metingen voor de eerste
twee soorten vogels de twee cumulatieve frequentiepolygonen in
de figuur hieronder. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
De verdeling van de
Reuzenalbatros is ongeveer een normale verdeling, die van de
Andescondor niet. |
| |
|
|
|
|
| |
a. |
Hoe noemen we de verdeling van de Andescondor? Leg duidelijk uit
of de mediaan van deze verdeling groter of kleiner zal zijn dan
het gemiddelde. |
| |
|
|
|
|
| |
b. |
Bepaal met de figuur (dus zonder GR) zo goed mogelijk de
standaardafwijking van de verdeling van de Reuzenalbatros. |
| |
|
|
|
|
| |
c. |
Bereken met je GR het gemiddelde en de standaardafwijking van de
vleugelspanwijdte Andescondor. |
| |
|
|
|
|
| |
Het totale onderzoek van de drie vogelsoorten omvatte 1176
vogels.
De verhouding tussen aantallen Andescondors en Reuzenalbatrossen
was 7 : 9
Voor elke 3 Reuzenalbatrossen waren er 4 Zeearenden. |
| |
|
|
|
|
| |
d. |
hoeveel vogels van elke soort er in het onderzoek waren. |
| |
|
|
|
|
| |
|
|
|
 |