© h.hofstede (h.hofstede@hogeland.nl)

De stelling van Napoleon.
     
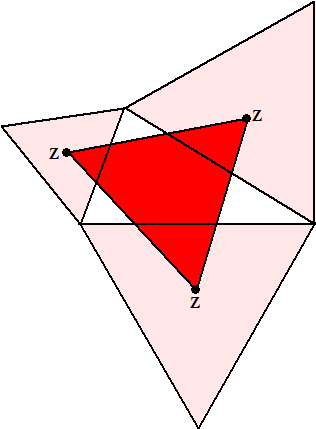
Jazeker!
Dit gaat over DÉ Napoleon!!

Die heeft  zowaar een stelling aan de vlakke meetkunde bijgedragen. en die stelling heet dan ook de "Stelling van Napoleon".

Nou kun je die bewijzen met een boel lastige sinus- en cosinusformules, maar ook heel eenvoudig met een paar simpele complexe getallen!  (mooi toch?  simpele complexe getallen?)

Eerst de stelling maar even:
       

Teken op de zijden van een driehoek drie gelijkzijdige driehoeken (allemaal aan de buitenkant of allemaal aan de binnenkant).

Dan vormen de zwaartepunten van die drie driehoeken wéér een gelijkzijdige driehoek!!

Zie de figuur hiernaast.
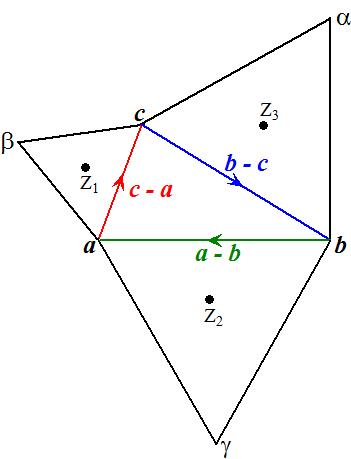
Die felrode driehoek daar in het midden  is dus weer gelijkzijdig.

 

       
Laten we de drie hoekpunten van de oorspronkelijke driehoek als drie getallen in het complexe vlak beschouwen.
Noem ze a , b en c

De zijden kun je als vectoren beschouwen, en die zijn dan 
a - b,  b - c  en  c - a

De nieuwe hoekpunten van de gelijkzijdige driehoek noemen we α, β en γ zoals in de figuur hiernaast.

Je komt bij β door de rode vector (c - a)  te draaien over 60º  (tegen de klok in) en die nieuwe vector bij a op te tellen.
Nou is draaien over 60º hetzelfde als vermenigvuldigen met het getal  z = 1/2 + 1/2i√3.  (in het vervolg noem ik dat gewoon z)
Dat betekent dat  β = a + z(c - a)
Op dezelfde manier geldt dan 
α = c + z(b - c)  en  γ = b + z(a - b)

Het zwaartepunt van een driehoek vind je door gewoon het gemiddelde van de drie hoekpunten te nemen. Laten we die zwaartepunten Z1, Z2 en Z3 noemen.

Dan geldt dus:
  Z1 = 1/3 • (a + c + a + z(c - a))
Z2 = 1/3 • (a + b + b + z(a - b))
Z3 = 1/3 • (b + c + c + z(b - c))
       
Als die drie Z's op een gelijkzijdige driehoek liggen, dan zou je bijvoorbeeld Z1 moeten krijgen door de vector (Z3 - Z2) over 60º te draaien en die dan bij Z2 op te tellen. Dus zou moeten gelden  Z1 = Z2 + z(Z3 - Z2)

Laten we gewoon kijken of dat klopt:
Z2 + z(Z3 - Z2)
=  1/3 • (a + b + b + z(a - b)) +  z( 1/3 • (b + c + c + z(b - c)) -  1/3 • (a + b + b + z(a - b)))
=  1/3 • (a + b + b + za - zb + zb + zc + zc + z2b - z2c - za - zb - zb - z2a + z2b)
=  1/3 • (a + 2b + 2zc + 2z2b  - z2c - z2a  - 2zb)

Nou eerst maar even z2 berekenen:   z2 =  (1/2 + 1/2i√3)2  = 1/4 + 1/2i√3 - 3/4  = -1/2 + 1/2i√3 = z - 1
Invullen:
Z2 + z(Z3 - Z2)
=  1/3 • (a + 2b + 2zc + 2(z - 1)b  - (z - 1)c - (z - 1)a  - 2zb)
=  1/3 • (a + 2b + 2zc +  2zb - 2b - zc + c -  za + a  - 2zb)
= 1/3 • (2a + zc + c - za)
= 1/3 • (a + c + a + z(c - a))
= Z1

Daarmee is de stelling van Napoleon bewezen!
       

© h.hofstede (h.hofstede@hogeland.nl)