| |
 |
|
Modulo-rekenen. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
|
|
Modulo-rekenen heet ook wel "klokrekenen".
En dat is niet zomaar natuurlijk.
Stel dat het op een moment 20 uur is (acht uur 's avonds), en je
telt daar 7 uur bij op. Dan zou het volgens "gewone" rekenmethodes dus
20 + 7 = 27 uur moeten zijn.
Maar niemand noemt dat 27 uur, iedereen zegt 3 uur. Dat komt natuurlijk
omdat het de volgende dag is geworden en die 24 uur van de vorige dag
interesseren ons niet zoveel meer.
Als het bijvoorbeeld 6 uur is, en je kijkt 132 uur later, dan is het
echt niet 138 uur, nee, je trekt daar de hele dagen die voorbij zijn
gegaan vanaf, dus het is dan 18 uur want er gaan 5 keer 24 uren van af.
Wat doe je dan eigenlijk?
Je kijkt hoe vaak 24 van 138 afgetrokken kan worden (de voorbijgegane
dagen). Dat is 5 keer, dus het is dan 138 - 5 24 = 18 uur.
Wiskundigen noemen dat modulo-rekenen, en noteren dat als: 138 (mod
24) = 18. Die 24 heet de "modulus".
Om voortaan duidelijk te maken dat we aan het modulorekenen zijn,
gebruiken we in plaats van de = nu een ☰ |
| |
|
|
|
Als je bijvoorbeeld
modulo-8 wilt rekenen, zul je in gedachten de klok hiernaast
gebruiken. Daaruit volgt bijvoorbeeld, dat (ga dat na!):
26 (mod 8) ☰ 2
-13 (mod 8) ☰ 3
257 (mod 8) ☰ 1
enz. |
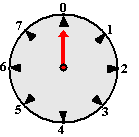 |
Er is ιιn verschil met een klok: |
|
Bij modulo-rekenen gaat het alleen om gehele
getallen |
|
| |
Eigenlijk is een
modulo-getal dus een hele verzameling getallen. Zo is 3 (mod 5) ☰ {...-7, -2, 3, 8, 13, 18, ....}
Het wordt ook wel een restklasse genoemd, immers 3 (mod
5) bestaat uit alle getallen die bij deling door 5 een rest van 3
opleveren.
Bij modulo-5 rekenen bestaan er dus eigenlijk maar 5 restklassen,
namelijk 0, 1, 2, 3 en 4.
Je zou natuurlijk net zo goed kunnen kiezen voor de getallen 5, 6,
7, 8 en 9 maar laten we afspreken dat we die modulo-getallen zo
eenvoudig mogelijk kiezen. |
| |
|
Modulo op de GR berekenen. |
| |
Kijk wat er gebeurt als je 23 (mod
5) uitrekent:
Je kijkt hoe vaak 5 in de 23 past, en dat is 4 keer. (23 : 5 = 4,6)
Dan haal je die 4 keer er af: 23 - 4 5 = 3.
Conclusie: 23 (mod 5) ☰ 3.
Bij grote getallen gaat het precies zo. Neem 1276345 (mod 1629)
Kijk hoe vaak 1629 in 1276345 past: 1276345 : 1629 = 783,514...
Haal er 783 keer 1629 van af: 1276345 - 783 1629 = 838.
Conclusie: 1276345 (mod 1629) ☰ 838.
Het mini-programmaatje op de GR hiernaast berekent ook A mod B op deze
manier. |
ClrHome
Prompt A
Prompt B
Disp (A - B * int(A/B)) |
|
| |
|
Rekenregels voor modulo-rekenen.
Om rekenregels af te leiden of
te bewijzen is het meestal handig om zo'n modulo-getal (zo'n restklasse)
toch weer te schrijven als een "gewoon" getal. Dat kan zσ: 3
(mod 5) = 3 + k 5 waarbij k een willekeurig
geheel getal is. Het voordeel van zo'n notatie is dat we met 3 + k
5 weer kunnen rekenen als met de "gewone" getallen die we al kennen.
slordige afspraak: in het vervolg noem ik zulke
getallen k, die elk geheel getal kunnen zijn allemaal k,
ook al zijn ze verschillend. Dus k + 3 = k
(immers als k een willekeurig geheel getal is, dan is k +
3 dat ook), en ook is k1 + k2
= k.
Genoeg afspraken, hoogste tijd voor de eerste stelling: |
| |
|
a (mod m) + b (mod
m) ☰ (a + b) (mod
m) |
|
| |
|
|
|
Haha! Een
ιιn-regelbewijs:
a(mod m) + b(mod m) = a + k1m
+ b + k2m = a + b + (k1
+ k2)m = a + b + k m
☰ (a + b) (mod m) |
| |
|
|
|
| Zo geldt bijvoorbeeld
68 (mod 12) + 125 (mod 12) ☰ 193 (mod 12) ☰ 1, en inderdaad is 8 + 5 =
13 Ί 1 (mod 12) |
| |
|
|
|
Meteen dan maar
kijken of het voor vermenigvuldigen ook geldt, vind je niet?
a (mod m) b(mod m) = (a + k1m)
(b + k2m) = ab + ak2m
+ bk1m + k1k2m2
= ab + m (ak2 + bk1+
k1k2m)
Dat laatste stuk is een geheel aantal keer m, dus dat kunnen we
best weer k m noemen.
Dan staat er ab + k m = ab (mod m). En dat
geeft de tweede stelling: |
| |
|
|
|
|
a
(mod m) b (mod
m) ☰ ab (mod m) |
|
| |
|
|
|
Dan kun je zo ook
kwadrateren: (a (mod m))2 ☰ (a
(modm)) (a (modm)) ☰ aa (modm) ☰
a2 (mod m)
En op dezelfde manier krijg je a3, a4,
a5 enz. Dus ook voor machtsverheffen
geldt: |
| |
|
|
|
|
|
| |
|
|
|
|
Snel machtsverheffen. |
| |
|
|
|
Deze regels voor
modulo-rekenen betekenen dat je erg snel kunt machtsverheffen, ook met
grote getallen. Door steeds tussendoor modulo m te
vereenvoudigen kun je grote getallen snel verkleinen, kijk maar:
Stel dat je wilt uitrekenen 332052 (mod 28)
Dat getal past niet op je GR, dus gewoon uitrekenen zal niet
lukken.
Maar 3320 (mod 28) = 16, dus dit is gelijk aan 1652 (mod
28). Dat past nog steeds niet op je GR
168 past er wιl op, dat is 4294967296, en (mod 28) is
dat gelijk aan 4.
(168)6 (mod 28) is dan gelijk aan 46
(mod 28) en dat is 8 en dat is dus al 1648
164 (mod 28) ☰ 16, dus 1652 (mod 28)
☰ 16 8 (mod 28) ☰ 128 (mod 28) ☰ 16
Conclusie: 332052 (mod 28) ☰ 16. |
| |
|
|
|
| |
|
|
|
|
| 1. |
Bereken: |
| |
|
|
|
|
| |
a. |
234 (mod 11) |
|
|
| |
b. |
123456789 (mod 14) |
|
|
| |
c. |
-56729034 (mod 2368) |
|
|
| |
|
|
|
|
| 2. |
Bereken: |
| |
|
|
|
|
| |
a. |
12675 (mod 56) |
|
|
| |
b. |
678569 (mod 1234) |
|
|
| |
c. |
14582345 (mod 1228) |
|
|
| |
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
Een toepassing:
Controlecijfers. |
| |
|
|
|
Nederlandse
bankrekeningnummers zijn niet zσmaar nummers....
De rekeningnummers bestaan allemaal uit 9 cijfers, maar het laatste van
die negen cijfers is een controlecijfer dat kijkt of het
opgegeven nummer wel een bankrekeningnummer kan zijn. Dat werkt zσ:
Stel het rekeningnummer is c1c2c3c4c5c6c7c8c9
Bereken dan 9 c1 + 8 c2 +
7 c3 + ... + 1 c9
Nu is c9 zσ gekozen dat, als je dit getal (mod
11) neemt, er nul uitkomt.
Neem bijvoorbeeld het bankrekeningnummer waarvan de eerste 8 cijfers zijn
45824365
Dan is 9 4 + 8 5 + 7 8 + ... + 2 5 = 204 en
204 mod 11 ☰ 6
Dus zal het laatste cijfer een 5 zijn, want er moet nog 5 bij om er 11
uit te krijgen.
De Belgen maken het nog bonter....
Daar bestaat een bankrekening uit 12 cijfers, maar nu zijn de laatste
twee cijfers zσ gekozen, dat het getal van de eerste 10 cijfers modulo
97 gelijk
is aan het getal van de laatste twee cijfers.
Dit principe van een controlegetal kom je bijvoorbeeld ook tegen bij het
ontwerpen van streepjescodes.
Elke keer als de kassajuffrouw voor jou een artikel scant wordt daar aan
modulorekenen gedaan! Kom je toch vaker tegen dan je had gedacht, nietwaar.....? |
| |
|
|
|
| |
|
|
|
|
| 3. |
a. |
Controleer of 455692634 een geldig
Nederlands rekeningnummer is. |
| |
|
|
|
|
| |
b. |
Een Nederlands bankrekeningnummer is
3446X8574. Bereken X. |
| |
|
|
|
|
| |
c. |
Een Belgisch rekening nummer begint met
2388453047 Bereken de laatste twee cijfers. |
| |
|
|
|
|
| |
|
|
|
|
| Nog een
toepassing: de datum van Paaszondag. |
| |
|
|
|
|
Paaszondag is de eerste zondag na de eerste
volle maan na 21 maart.
Waarom na 21 maart?
21 maart wordt gebruikt als de "Equinox" = de datum waarop dag
en nacht even lang zijn (de werkelijke equinox kan 1 of 2
dagen verschillen)
Nou herhalen de data van volle maan zich heel nauwkeurig om de
19 jaar. Daarom kun je de datum van paaszondag als volgt
berekenen:
Bereken (jaartal mod 19) + 1
Zoek die waarde in onderstaande tabel op.
Paaszondag is de eerste zondag na de datum uit de tabel. |
| |
|
|
|
|
| 0 |
27 maart |
| 1 |
14 april |
| 2 |
3 april |
| 3 |
23 maart |
| 4 |
11 april |
| 5 |
31 maart |
| 6 |
18 april |
| 7 |
8 april |
| 8 |
28 maart |
| 9 |
16 april |
| 10 |
5 april |
| 11 |
25 maart |
| 12 |
13 april |
| 13 |
2 april |
| 14 |
22 maart |
| 15 |
10 april |
| 16 |
30 maart |
| 17 |
17 april |
| 18 |
7 april |
| 19 |
27 maart |
|
| |
|
|
|
|
Het kan ook zonder zo'n lelijke tabel en zonder
nog weer te moeten kijken wanneer de eerstvolgende zondag is.
Gauss ontwikkelde het volgende algoritme: ( ↓ betekent: naar
beneden afronden op geheel getal). |
| |
|
|
|
|
| |
 |
| a = jaartal mod 19 |
| b = jaartal mod 4 |
| c = jaartal mod 7 |
| k = jaartal/100
↓ |
| p = (13 + 8k)/25
↓ |
| q = k/4
↓ |
| M ☰ (15 - p + k - q)
mod 30 |
| N ☰ (4 + k - q) mod 7 |
| d ☰ (19a + M) mod 30 |
| e ☰ (2b + 4c + 6d +
N) mod 7 |
Paaszondag is
(22 + d + e maart) OF
(d + e - 9 april) |
| als d = 29 en e = 9 vervang
dan 26 april door 19 april. |
| als d = 28 en e = 6 en (11M + 11
mod 30) < 19, vervang dan 25 april door 18
april. |
|
| |
|
|
|
|
Voorbeeld voor het jaar 2019:
a = 5
b = 3
c = 3
k = 20
p = 6
q = 5
M = 24
N = 5
d = 29
e = 1
29 + 1 - 9 april = 21 april. |
| |
|
|
|
|
| |
| |
|
|
|
|
| |
|
|
|
 |
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|