| 1. |
Het aantal mobieltjes in Nederland neemt
sterk toe. Een conciërge van een middelbare school heeft een
poosje bijgehouden hoeveel mobieltjes er waren onder de leerlingen.
Voor de eerste vijf maanden vond hij de volgende tabel: |
|
|
|
|
|
|
| maand t |
1 |
2 |
3 |
4 |
5 |
| aantal A |
20 |
24 |
30 |
37 |
45 |
|
|
|
|
|
|
|
De man heeft wiskunde in zijn pakket
gehad en ontwikkelt de formule A(t) = 16 • 1,22t |
|
|
|
a. |
In welke maand wijkt het voorspelde
aantal procentueel het meest af van het werkelijke aantal?
|
| |
|
|
|
|
b. |
Bereken met deze formule wanneer er voor
het eerst 700 mobieltjes zullen zijn. |
|
|
|
Maar dat is nou net het probleem: de
school heeft maar 600 leerlingen, dus het model van de conciërge
kan nooit kloppen. Haastig en met een rood hoofd stelt de man een
nieuwe formule op:
|
|
| c. |
Is deze formule voor de eerste 5 maanden
slechter of beter dan de eerste formule? |
| |
|
|
| d. |
Bereken met deze formule wanneer er voor
het eerst 400 mobieltjes zullen zijn. |
|
| |
|
|
| e. |
Onderzoek wanneer beide modellen een
verschil van ongeveer 120 mobieltjes geven. |
|
| |
|
|
| f. |
Zullen er
volgens deze tweede formule op deze school ooit 400 mobieltjes
komen? en 450? en 500? |
|
|
|
|
|
|
|
| 2. |
Heineken houdt een korte maar intensieve
reclamecampagne om de verkoop in België te stimuleren. Zoals
verwacht neemt de verkoop van Heineken bier direct na aanvang van
de reclamecampagne toe. Echter, zodra men stopt met de campagne in
België neemt die verkoop langzaam weer af. Belgische reclame- en
bierexperts hebben aan de hand van ervaringen met eerdere
reclamecampagnes het volgende model opgesteld:
|
|
Daarin is L het aantal liter bier
per maand en t de tijd in maanden met t = 0 het
tijdstip van de start van de campagne. |
|
|
|
|
|
|
a. |
Na hoeveel maanden zal men 900000
liter per maand verkopen? |
|
| |
|
|
|
|
b. |
Na hoeveel maanden stopt men met de
campagne? Hoe groot is de verkoop op dat moment? |
|
| |
|
|
|
|
c. |
Op welk moment verkoopt men evenveel als
in het begin? |
|
| |
|
|
|
|
d. |
Hoe groot zal de verkoop op de lange
duur worden? |
|
|
|
|
|
|
| 3. |
Vroeger als student vond ik het
regelmatig erg leuk om rauwe eieren vanaf een verdieping van de
studentenflat naar beneden te gooien. Als je die in het gras gooit
dan kunnen ze nog vanaf erg grote hoogte heel blijven.
Een groot aantal metingen leverde mij de volgende tabel. |
|
|
|
|
|
|
| verdieping V |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| percentage P |
100 |
66 |
52 |
41 |
32 |
24 |
16 |
10 |
3 |
0 |
|
|
|
|
|
|
|
V is het verdiepingnummer
van waaraf de eieren gegooid worden, P is het percentage eieren
dat de val overleeft. |
|
|
|
|
|
|
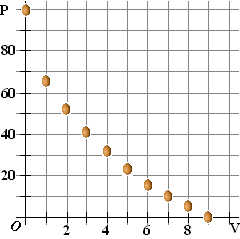
Een grafiek van
de door mij gevonden meetwaarden zie je hiernaast. Ik
probeer het volgende wiskundige model:
|
|
|
|
|
|
a. |
Onderzoek bij welke
meetwaarde deze formule model
het meest afwijkt (absoluut) van de gemeten waarde |
|
|
|
|
|
|
Elke verdieping is 3,60
meter hoog, en daarom kan ik de bovenstaande formule veranderen in |
|
|
|
|
|
|
|
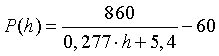
|
|
|
|
|
|
|
b. |
Leg uit waar dat getal 0,277
vandaan komt. |
| |
|
|
|
c. |
Vanaf welke hoogte zou
volgens dit model 80% van de eieren overleven? |
|
|
|
|
|
|
Mijn collega komt met een
ander model. Zij beweert dat geldt: P(h)
= 100 - 18√h |
|
|
|
|
|
|
d. |
Vind je haar model beter of
slechter dan het mijne? Leg uit waarom. |
| |
|
|
|
e. |
Vanaf welke hoogte zou
volgens dit model 80% van de eieren overleven? |
| |
|
|
|
f. |
Zijn er hoogtes waarop onze
modellen precies hetzelfde percentage voorspellen? Zo ja, Welke
zijn dat? |
|
|
|
|
| |
|
|
Een andere collega gaat zich
er ook met bemoeien. Hij vindt dat de ei-grafiek hierboven de vorm
van een parabool heeft, en stelt het volgende model
voor: P(h) = a •
h2
+ b •
h + c |
|
|
|
|
|
|
g. |
Omdat het model in ieder
geval bij h = 0 moet opleveren P = 100 kun je c al
berekenen. Doe dat. |
| |
|
|
|
h. |
Omdat dit model ook nul
oplevert bij de negende verdieping (h = 32,4) zou je kunnen
eisen dat de top van die parabool bij (32.4, 0) ligt.
Zoek uit voor welke a en b dit model daarmee
klopt. |
| |
|
|
|
|
|
|
|
|
|
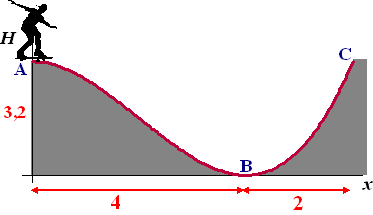
| 4. |
Hiernaast is
het zijaanzicht van een skatebaan getekend. Deze baan begint in punt
A en eindigt in punt C, zes meter horizontaal vanaf A
De formule die de vorm van de baan beschrijft is:
H(x) = 0,1x3 – 0,6x2 +
3,2
Bereken voor welke waarden van x de baan lager dan 2 meter
is. |
 |
| |
|
|
|
| |
|
| 5. |
De verkoop van Italiaans ijs
in Nederland gedurende één jaar wordt aardig beschreven door de
volgende formule:
Y(w) = 5,5w3 - 450w2
+ 8600w + 70000
Daarin is Y de hoeveelheid verkocht ijs (in liter)
en w het weeknummer, met week 0 van 21 tm 27 maart.
|
|
|
|
|
|
| |
a. |
In hoeveel weken werd er
meer dan 90000 liter ijs verkocht? |
|
|
|
|
|
| |
b. |
Bereken hoeveel liter
verschil er tussen de maximale en de minimale ijsverkoop is. |
| |
|
|
|
|
| |
|
|
|
|
| 6. |
examenvraagstuk VWO
Wiskunde A, 1983. |
| |
|
|
|
|
| |
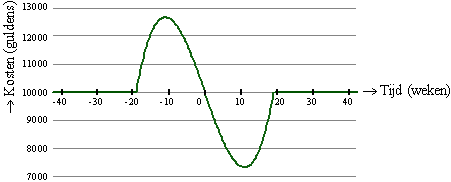
De voorraadkosten van een verffabriek
vertonen in de jaren 1981/1982 het volgende verloop: |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
Het normale niveau van de voorraadkosten
bedraagt f 10000,-
Het punt 0 op de horizontale as correspondeert met 1 april 1982.
De kostenverandering hing samen met een voor het voorjaar 1982
voorziene, tijdelijke productieverhoging. |
| |
|
|
|
|
| |
a. |
In welke maand (en welk
jaar) begonnen de voorraadkosten af te wijken van het normale
niveau? |
| |
|
|
|
|
| |
Een medewerker heeft voor
het gedeelte van de grafiek dat een afwijking van het normale niveau
laat zien, een formule opgesteld: V = t3 -
363t + 10000 (V = voorraadkosten in
guldens, t = tijd in weken)
Ga bij de beantwoording van de vragen b en c uit van deze
formule. |
| |
|
|
|
|
| |
b. |
Op welk tijdstip t
begint (respectievelijk eindigt) de afwijking van het normale
niveau? |
| |
|
|
|
|
| |
c. |
Bereken hoeveel procent de
maximale afwijking van het normale niveau bedroeg. |
| |
|
|
|
|
| |
|
|
|
|
| 7. |
examenvraagstuk Wiskunde
A, VWO, 1984 Door een technische storing in de
air-conditioning van een groot gebouw neemt het zuurstofgehalte
tijdelijk af.
De technische staf heeft het verloop van het zuurstofgehalte
beschreven met het volgende model: |
| |
|
|
|
|
| |
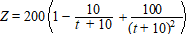 |
| |
|
|
|
|
| |
Hierin is t de tijd in minuten,
gerekend vanaf het moment dat de storing begon, en is Z het aantal
cm3 zuurstof per liter lucht op tijdstip t. Op het
moment t = 0 is het zuurstofniveau normaal. |
| |
|
|
|
|
| |
a. |
Na verloop van tijd nadert
het zuurstofgehalte weer tot het normale niveau. Toon aan dat het
gekozen model hiermee in overeenstemming is. |
| |
|
|
|
|
| |
b. |
Bereken in het model het
tijdstip waarop het zuurstofgehalte minimaal is. |
| |
|
|
|
|
| |
c. |
Iemand beweert dat het
zuurstofgehalte 1 uur na het begin van de storing op 90% van het
normale niveau is. Onderzoek of die uitspraak klopt met het model. |
| |
|
|
|
|
| |
d. |
De medische
staf vindt een zuurstofgehalte van 80% van het normale niveau nog
net toelaatbaar.
Bereken in één decimaal nauwkeurig het aantal minuten dat, volgens
het model, het zuurstofgehalte ontoelaatbaar laag is. |
| |
|
|
|
|
| |
e. |
Een
ander model ziet er zó uit: |
| |
|
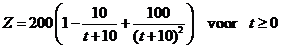 |
| |
|
|
|
|
| |
|
Bereken voor
welke t beide modellen het grootste verschil voor Z
opleveren. |
| |
|
| |
|
| 8. |
Examenvraagstuk HAVO wiskunde A, 2007. Een hardloopster is gespecialiseerd op
de 100 meter. Bij dit atletiekonderdeel moet je zo
snel mogelijk je topsnelheid halen en die dan proberen vast te houden
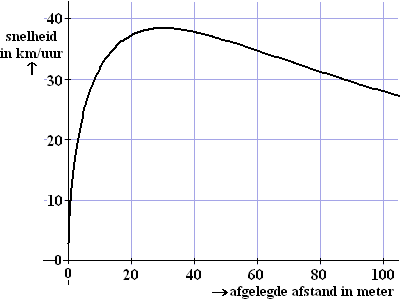
tot de finish. Haar trainer heeft haar sprint laten
onderzoeken met behulp van supersnelle camera’s.
In onderstaande figuur is het verband tussen de snelheid en
de afgelegde afstand in een grafiek
weergegeven. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
Op verzoek van de trainer heeft een
wiskundige een formule gemaakt die goed past bij deze
grafiek.
Die formule is: |
| |
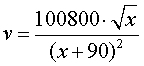 |
| |
|
|
|
|
| |
In deze formule is v de
snelheid in kilometer per uur en x de
afgelegde afstand in meter.
In de eerste figuur zie je dat de
maximale snelheid ongeveer 38 km per uur is en de snelheid
bij de finish ongeveer 28 km per uur. |
| |
|
|
|
|
| |
a. |
Bereken met welke snelheid de
hardloopster volgens de formule de finish passeert.
Geef je antwoord in één decimaal. |
| |
|
|
|
|
| |
b. |
Bereken de hoogste snelheid die de
hardloopster bereikt volgens de formule. Geef
je antwoord in één decimaal. |
| |
|
|
|
|
| |
In de grafiek zie je dat de snelheid
tijdens een gedeelte van de sprint hoger dan 35
km per uur is. |
| |
|
|
|
|
| |
c. |
Bereken met behulp van de formule
hoeveel meter de hardloopster aflegt met een
snelheid die hoger is dan 35 km per uur. |
| |
|
|
|
|
| |
|
|
|
|
| 9. |
Examenvraagstuk HAVO Wiskunde B, 2007.
(gewijzigd) |
| |
|
|
|
|
| |
Een mobiele telefoon werkt op
een batterij. Zo'n telefoon kan vrij lang aanstaan als je niet belt. De
maximale tijd dat de mobiele telefoon aan kan staan zonder gebruikt te
worden heet de stand-by tijd. Als je wel belt, verbruikt de telefoon meer
energie. De batterij is dan sneller leeg.
Bij een telefoon op stand-by stand met een moderne batterij wordt
het spanningsverloop benaderd door de formule:
|
| |
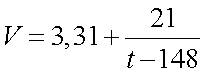 |
| |
|
|
|
|
| |
Hierin is V de spanning van de batterij in Volt en t de
tijd in uur.
Op tijdstip t = 0 is de batterij vol.
De telefoon staat vanaf het ogenblik waarop de batterij net helemaal is
opgeladen stand-by totdat de spanning tot 0 is gedaald. In minuten
nauwkeurig is deze stand-by-tijd gelijk aan 141 uur en 39
minuten. |
| |
|
|
|
|
| |
a. |
Bereken deze
tijd in seconden nauwkeurig. |
| |
|
|
|
|
| |
De spanning die de batterij
levert kun je aan de rechterkant van het scherm aflezen. Daar zijn
vier blokjes die aan of uit kunnen staan. Als de batterij vol is, staan
alle blokjes (nummers 1 t/m 4) aan.
Bij een volle batterij bedraagt de spanning ongeveer 3,2 Volt.
Het aantal blokjes dat 'aan' staat wordt bepaald door het percentage van
de maximale spanning. Als het percentage minder dan 75% bedraagt kan er
niet meer getelefoneerd worden en zijn alle blokjes uit. Zie onderstaande
tabel. |
| |
|
|
|
|
| |
| blokjes die zichtbaar zijn |
percentage van de
maximale spanning |
| 1,2,3,4 |
100 - 97 |
| 2,3,4 |
97 - 94 |
| 3,4 |
94 - 88 |
| 4 |
88 - 75 |
| geen |
75 - 0 |
|
| |
|
|
|
|
| |
Iemand laadt de batterij
helemaal op. Vervolgens legt hij de telefoon in de stand-by stand weg. De
telefoon wordt niet gebruikt. Na verloop van tijd gaat blokje nummer 1
uit. Een tijd nadat blokje nummer 1 is uitgegaan, gaat blokje nummer 2
uit. Juist op dat moment pakt hij de telefoon, ziet blokje nummer 2
uitgaan en denkt dat de telefoon op de helft van zijn stand-by tijd is. Er
zijn dan immers nog twee blokjes (nummer 3 en 4) van de vier zichtbaar |
| |
|
|
|
|
| |
b. |
Onderzoek met behulp van de gegeven formule
of de telefoon op het moment dat blokje nummer 2 uitgaat, op de helft van
zijn stand-by tijd is. |
| |
|
|
|
|
| 10. |
Examenvraagstuk VWO Wiskunde A,
2006
In de volgende tabel staan de
wereldrecords hardlopen bij de mannen tot en met september 2003 op een
aantal afstanden. |
| |
|
|
|
|
| |
| Afstand (in meters) |
Tijd |
Gemiddelde snelheid (in km/uur) |
100
200
400
800
1000
1500
2000
3000
5000
10 000 |
9.78
19.32
43.18
1 : 41.11
2 : 11.96
3 : 26.00
4 : 44.79
7 : 20.67
12 : 39.36
26 : 22.75 |
36,8
37,3
33,3
28,5
27,3
26,2
25,3
24,5
23,7
22,7 |
|
| |
|
|
|
|
| |
In de tabel zie je bijvoorbeeld
dat het wereldrecord op de 1000 meter 2 : 11,96 was. dat betekent 2
minuten en 11,96 seconden. Afgerond op één
decimaal was daarbij de gemiddelde snelheid 27,3 km/uur.
Het verband tussen de afstanden en de gemiddelde snelheid uit de
tabel kunnen we benaderen met de volgende formule:
|
| |
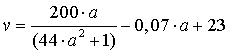 |
| |
|
|
|
|
| |
In deze formule is v de gemiddelde snelheid in km/uur en a
de afstand in kilometer.
De gemiddelde snelheden volgens deze formule komen niet precies overeen
met de uitkomsten uit de bovenstaande tabel. |
| |
|
|
|
|
| |
a. |
Bereken voor de 3000 meter (dus a =
3) hoeveel de gemiddelde snelheid volgens de formule afwijkt van de
uitkomst uit de tabel. |
| |
|
|
|
|
| |
Met deze formule kun
je bij elke afstand boven de 100 meter de gemiddelde snelheid berekenen
die hoort bij het denkbeeldig gelopen wereldrecord. Voor bijvoorbeeld een
afstand van 2283 zou het wereldrecord met een gemiddelde snelheid van
24,82 km/uur zijn gelopen. |
| |
|
|
|
|
| |
b. |
Bereken op welke afstand het denkbeeldige
wereldrecord een gemiddelde snelheid van precies 30 km/uur op zou leveren. |
| |
|
|
|
|
| |
In de tabel is de gemiddelde
snelheid het hoogst bij de 200 meter. De formule van v is niet
maximaal bij de 200 meter maar bij een afstand tussen de 100 en 200 meter. |
| |
|
|
|
|
| |
c. |
Bereken in meters nauwkeurig bij welke
afstand de gemiddelde snelheid zo groot mogelijk is volgens de formule van
v |
| |
|
|
|
|
| |
|
|
|
|
 |
|
 |