| |
|
 |
| 1. |
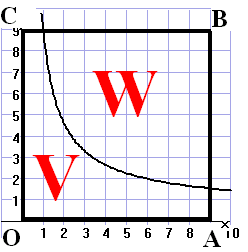
De punten O, A(9,0) en C(0,9)
zijn hoekpunten van een vierkant OABC. |
| |
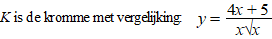 |
| |
De kromme K verdeelt het vierkant in de
delen V en W. |
| |
|
|
| |
a. |
Bereken in drie decimalen nauwkeurig de
oppervlakte van beide delen. |
| |
|
|
| |
b. |
Het omwentelingslichaam L1
ontstaat door vlakdeel V om de x-as te wentelen. Bereken de
inhoud van L1 in twee decimalen nauwkeurig |
| |
|
|
|
| |
c. |
Het omwentelingslichaam L2
ontstaat door vlakdeel W om de lijn y = 9 te wentelen. Pas een
handige translatie toe en bereken de inhoud van L2. |
| |
|
|
|
| |
d. |
De lijn y = x
verdeelt vlakdeel V in twee delen. Bereken de inhoud van het
omwentelingslichaam dat ontstaat als het rechterdeel
wordt gewenteld om de x-as. Geef je antwoord in 2 decimalen
nauwkeurig. |
| |
|
|
|
| 2. |
Het vlakdeel,
ingesloten door de grafieken van y = x2 - 2x
en y = x wordt gewenteld om de lijn y =
4.
Bereken algebra´sch de inhoud van het omwentelingslichaam dat dan
ontstaat. |
| |
|
|
|
| |
|
|
|
| 3. |
examenvraagstuk
VWO Wiskunde B, 1993. Gegeven is de functie f:
x → x + 3 - 4√x
met domein [0, →〉
Ten opzichte van een assenstelsel Oxy is K de grafiek van f.
V is het vlakdeel
begrensd door K en de lijn y = 3.
Bereken in gehelen
nauwkeurig de inhoud van het lichaam dat ontstaat door V te wentelen om
de lijn y = 3. |
| |
|
|
|
| 4. |
examenvraagstuk
VWO Wiskunde B, 1997. |
| |
|
|
|
| |
Met domein [-3, →〉
is gegeven de functie
f: x → x√(x
+ 3)
en
met domein [-3, →〉
\ {0} de functie |
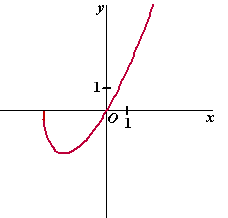 |
| |
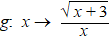 |
| |
De grafiek van f is in de
figuur hiernaast getekend. |
| |
|
|
| |
a. |
Bereken het bereik van f. |
| |
|
|
| |
b. |
Bereken de co÷rdinaten van de
gemeenschappelijke punten van de grafieken van f en g. |
| |
|
|
|
| |
Het gesloten vlakdeel begrensd
door de grafieken van f en g wordt gewenteld om de x-as. |
| |
|
|
|
| |
c. |
Bereken de inhoud van het
omwentelingslichaam dat zo ontstaat. |
| |
|
|
|
| 5. |
De functie f is gegeven door f (x)
= √(1 − x) .
In de figuur hiernaast zijn op het interval [0, 1] de grafiek van f
en de lijn y = x getekend.
Het gebied V wordt
begrensd door de grafiek van f, de y-as, de lijn y
= x en de lijn x = 1/2.
Zie de figuur hiernaastBereken exact de inhoud van het
omwentelingslichaam dat ontstaat wanneer V om de x-as wordt
gewenteld. |
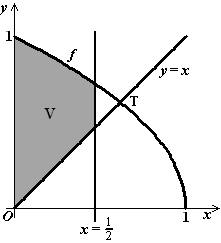 |
| |
|
|
|
| |
|
|
|
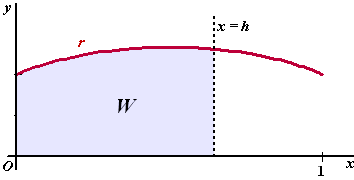
| 6. |
Op het domein [0, 1] is de functie
r
gegeven door
r(x)
= 1/10
Ľ √(5 + 15x - 15x2).
W is
het vlakdeel dat wordt ingesloten door de
x-as,
de y-as,
de grafiek van r
en de lijn
x
=
h
, met
0
<
h ≤1.
Zie de figuur.
Voor het volume V
van het
omwentelingslichaam dat ontstaat door vlakdeel
W
om de
x-as
te wentelen, geldt: |
 |
| |
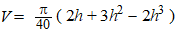 |
| |
|
|
|
| |
a. |
Toon aan dat deze formule voor
V juist is. |
|
| |
|
|
|
| |
Als de grafiek van
r om de
x-as
gewenteld wordt, ontstaat een figuur die lijkt op een regenton. Voor
x,
h
en
r
nemen we de meter als eenheid,
zodat de ton 1 meter hoog is.
V
is dus het volume van het water in
de ton als het water h
meter hoog staat. |
 |
| |
|
|
| |
b. |
Bereken de waterhoogte in de ton als deze voor drie
vierde deel is gevuld. Rond je antwoord af op een geheel aantal cm. |
| |
|
|
|
| 7. |
examenvraagstuk
VWO Wiskunde B, 2013. |
| |
|
|
|
| |
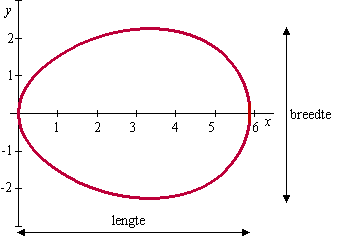
De functie f is gegeven door f(x)
= 1/6√(87x-
3x2 - 2x3)
In onderstaande figuur is de grafiek van f getekend en
ook het spiegelbeeld hiervan in de x-as. De twee grafieken
vormen samen een figuur die lijkt op een doorsnede van een ei.
Op de
x-as en de
y-as
is de eenheid 1 cm. In de figuur is aangegeven wat bedoeld wordt met
de lengte en de breedte van het ei. De lengte van het ei is ongeveer
5,9 cm. |
 |
| |
|
|
| |
a. |
Bereken op algebra´sche wijze de lengte van het ei
in cm. Rond je antwoord af op twee decimalen. |
| |
|
|
| |
b. |
Bereken met behulp van primitiveren de inhoud van
het ei. Geef je antwoord in een geheel aantal cm3. |
| |
|
|
|
| |
|
|
|
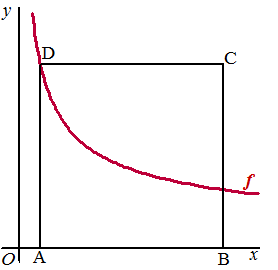
| 8. |
De functie f is gegeven door f(x)
= 16/√x
Van vierkant ABCD liggen de hoekpunten A
en B op de x-as en het hoekpunt D op de
grafiek van f.
Zie de figuur hiernaast.
De x - co÷rdinaat van A is gelijk aan 1
V is het deel van dit vierkant dat zich boven de grafiek
bevindt.
Vlakdeel V wordt gewenteld om de x-as. Bereken exact de inhoud van het
bijbehorende omwentelingslichaam. |
 |
| |
|
|
|
| |
|
|
|
| 9. |
Examenvraagstuk
VWO Wiskunde B, 2017-I |
| |
|
|
|
| |
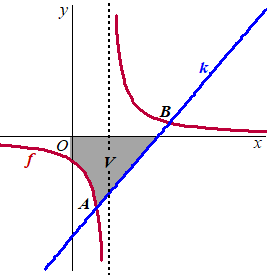
De functie f
wordt gegeven door: f(x) = 5/(4x
- 6)
De lijn k met vergelijking y
=
x
-
31/2
snijdt de grafiek van f in twee punten, A
en B. Zie de figuur.
De co÷rdinaten van punt A zijn (1, -21/2) |
 |
| |
|
|
| |
a. |
Bereken exact de co÷rdinaten van punt B. |
| |
|
|
| |
Het vlakdeel V wordt ingesloten door de
grafiek van f , de x-as, de y-as en de lijn
k. In de figuur hiernaast is dit vlakdeel grijs gemaakt.
V wordt gewenteld om de x-as. Zo ontstaat een
omwentelingslichaam. |
| |
|
|
|
| |
b. |
Bereken exact de inhoud van dit omwentelingslichaam. |
| |
|
|
|
| 10. |
Examenvraagstuk
VWO Wiskunde B, 2019-I De functie
f
is gegeven
door
f
(x)
=
√x.
De grafiek van
f
is getekend
in de figuur linksonder, samen met de lijnen
met vergelijkingen
x
=
a en
x
=
b
, waarbij
0
<
a
<
b
. Midden
tussen de punten
(a,
0) en
(b,
0) ligt het punt
(m,
0) .
De grafiek van
f,
de
x-as
en de twee verticale lijnen sluiten een
gebied in.
Dit gebied, in de figuur linksonder met
groen aangegeven, wordt gewenteld om de
x-as.
Het omwentelingslichaam is een zogenaamde
afgeknotte parabolo´de.
Deze is afgebeeld in de figuur rechtsonder. |
| |
|
|
|
| |
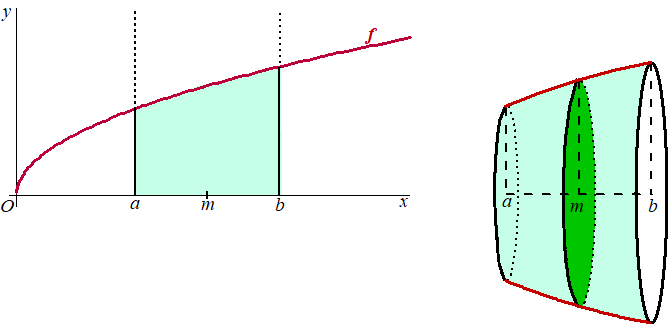 |
| |
|
|
|
| |
Bij de omwenteling
beschrijft elk punt van de grafiek een
cirkel.
De oppervlakte van de cirkel die beschreven
wordt door het punt
(m,
m)
noemen we
A. De
cirkelschijf met deze oppervlakte is met
donkergroen aangegeven in de rechterfiguur. |
| |
|
|
|
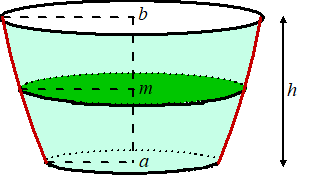
| |
In de figuur hiernaast staat
de afgeknotte parabolo´de een kwartslag
gedraaid. In die figuur is ook de hoogte
h van de
afgeknotte parabolo´de aangegeven.
Voor de inhoud
V van de
afgeknotte parabolo´de geldt de formule:
V
=
h
Ľ
A
Bewijs dit. |
 |
| |
|
|
|
| |
|
|
|
| |
|
|
 |
|
ę h.hofstede (h.hofstede@hogeland.nl)
|