|
|||||
| 1. | a. | Y1 = (4X + 5)/(X√(X))
en Y2 = 9 en dan intersect geeft x = 1 Vlakdeel V kun je door de lijn x = 1 te tekenen verdelen in een rechthoek van 1 bij 9 plus een deel onder de grafiek van f Dat deel loopt van x = 1 tot x = 9 Y1 = (4X + 5)/(X√(X)) en dan calc - ∫f(x)dx van (X = 1) tot (X = 9) geeft oppervlakte 22,667 De totale oppervlakte is dan 31,667 Het andere deel heeft dan oppervlakte 81 - 31,667 = 49,333 |
|||
| b. | Y1 = (4X + 5)/(X√(X))
Y2 = π • Y1^2 calc - ∫f(x)dx van Y2 van (X = 1) tot (X = 9) geeft inhoud 260,93 Het stuk tussen x = 0 en x = 1 omwentelen geeft een cilinder met inhoud π• 92 • 1 = 254,47 De totale inhoud wordt dan 515,40 |
||||
| c. | Schuif de grafiek 9
omlaag en wentel dan om de x-as. Y1 = (4X + 5)/(X√(X)) Y2 = π • Y1^2 calc - ∫f(x)dx van Y2 van (X = 1) tot (X = 9) geeft inhoud 1014,91 |
||||
| d. | Y1 = (4X + 5)/(X√X))
Y2 = X intersect levert snijpunt (3.1489, 3.1489) Het vlakdeel bestaat uit een driehoek en een deel onder de grafiek van f de driehoek omwentelen levert een kegel met inhoud 1/3 • π • 3,14892 • 3,1489 = 32,70 het deel onder de grafiek van f omwentelen: Y1 = (4X + 5)/(X√X)) Y2 = π • Y1^2 calc - ∫f(x)dx van Y2 van (X = 3,1489) tot (X = 9) geeft inhoud 82,21 Samen geeft dat een inhoud van 114,91 |
||||
| 2. | x2 - 2x = x x2 - 3x = 0 x(x - 3) = 0 x = 0 ∨ x = 3 Schuif alles 4 omlaag, dan kun je wentelen om de x-as De formules worden dan y = x2 - 2x - 4 en y = x - 4 |
||||
|
|
|||||
|
|
|||||
| De inhoud daartussen is dan 51,6π - 21π = 30,6π | |||||
| 3. | x + 3 - 4√x
= 3 x - 4√x = 0 √x(√x - 4) = 0 √x = 0 ∨ √x = 4 x = 0 ∨ x = 16 Schuif alles 3 omlaag dan kun je wentelen om de x-as De formule wordt dan y = x - 4√x |
||||
|
|
|||||
| 4. | a. | Zoek het minimum van f f ' = 1 • √(x + 3) + x • 1/2√(x + 3) = 0 vermenigvuldig met 2√(x + 3), dan krijg je 2x + 6 + x = 0 3x = -6 ⇒ x = -2 ⇒ y = -2 • √1 = -2 Het bereik van f is dus [-2, →〉 |
|||
| b. | x√(x
+ 3) = √(x + 3)/x x2 √(x + 3) - √(x + 3) = 0 (en x ≠ 0) √(x + 3) • (x2 - 1) = 0 √(x + 3) = 0 ∨ x2 - 1 = 0 x = -3 ∨ x = 1 ∨ x = -1 Dat geeft de punten (-3, 0) en (-1, -√2) en (1, 2) |
||||
| c. | Het vlakdeel zit tussen x = -3 en x = -1 (zie de figuur) |
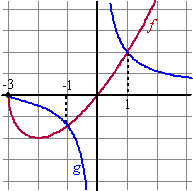 |
|||
|
|
|||||
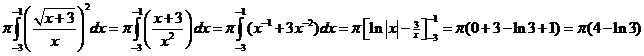 |
|||||
| Het verschil is dan π • (2 + ln3) | |||||
| 5. | Wentel eerst het hele gebied onder de grafiek van f tussen x = 0 en x = 1/2 om de x-as: | ||||
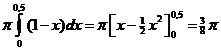 |
|||||
| Trek nu de kegel die
ontstaat door het driehoekje onder de grafiek van f om de x-as
te wentelen er weer af. Die kegel heeft inhoud 1/3 • π • 0,52 • 0,5 = 1/24π Dan houd je over 3/8π - 1/24π = 1/3π |
|||||
| 6. | a. |
|
|||
| deel alles door 2,5 en je hebt de gevraagde formule. | |||||
| b. | h = 1
geeft V = 3p/40
en dan is de ton helemaal vol. neem daar 3/4 deel van: V = 9/160π Y1 = π/40 • (2X + 3X2- 2X3 ) Y2 = 9/160π intersect levert dan h = 0,72 dus dat is 72 cm |
||||
| 7. | a. | f(x)
= 0 87x - 3x2 - 2x3 = 0 x(87 - 3x - 2x2) = 0 x = 0 ∨ x = (3 ±√(9 + 4•87•2))/-4 = (3 ±√(705))/-4 x = 0 ∨ x = 5,89 ∨ x = -7,39 De nulpunten zijn x = 0 en x = 5,89 dus de lengte is 5,89 cm. |
|||
| b. |
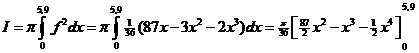 |
||||
| =
π/36• { (87/2•5,92
- 5,93 - 1/2•5,94)
- (0) } = 61,34 cm3 dus dat is ongeveer 61 cm3 |
|||||
| 8. | Eerst
het deel onder de grafiek wentelen om de x-as: I = π • ∫(256/x)dx = π • [256 • lnx] Het vierkant heeft zijden 16, dus grenzen 17 en 1 invullen: I = π(256ln17 - 256ln1) = 256πln17 DC wentelen om de x-as geeft een cilinder met inhoud π • 162 • 16 = 4096π Het gevraagde omwentelingslichaam heeft inhoud 4096π - 256πln17 |
||||
| 9. | a. | x
- 31/2
= 5/(4x - 6) (4x - 6)(x - 31/2) = 5 4x2 - 14x - 6x + 21 = 5 4x2 - 20x + 16 = 0 x2 - 5x + 4 = 0 (x - 1)(x - 4) = 0 x = 1 ∨ x = 4 B is het punt (4, 1/2) |
|||
| b. | Splits
het vlakdeel in twee delen: van O tot A en van A tot
de x-as A = (1, -21/2) linkerdeel: |
||||
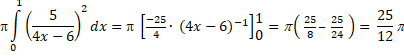 |
|||||
| rechterdeel: een kegel met straal grondvlak 21/2 en hoogte 21/2. Inhoud 1/3 • π(21/2)2 • 21/2 = 125/24π Samen geeft dat inhoud 175/24π |
|||||
| 10. |
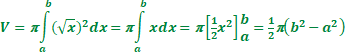 |
||||
| m
= 1/2(a + b) dus A =
π(√m)2
=
πm =
1/2π(a
+ b) h = b - a dus hA = (b - a) • 1/2π (a + b) hA = 1/2π (ba + b2 - a2 - ab) hA = 1/2π(b2 - a2) en dat is inderdaad gelijk aan bovenstaande integraal. |
|||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||