| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
| |
|
|
|
| 1. |
Examenvraagstuk
HAVO Wiskunde A, 2009 Voordat je met verven begint, wil je
natuurlijk weten hoeveel (blikken) verf je nodig hebt. Afhankelijk van het soort kwast dat wordt gebruikt, verlies je
tussen de 5 en 10 procent van de verf. Het verband tussen deze zaken
staat in de volgende formule, waarin ook
rekening is gehouden met verlies van verf door gebruik van de kwast: |
| |
|
|
|
| |
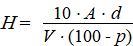 |
| |
|
|
|
| |
Hierin is:
− H de hoeveelheid verf (in liter);
− A de oppervlakte (in m2);
− d de dikte van de verflaag (in micrometer);
− V het percentage vaste stof;
− p het verliespercentage bij kwasten; dit varieert van 5 tot 10.
De verf die je wilt gebruiken, wordt verkocht in blikken van 2,5 liter.
Op de blikken staat dat het percentage vaste stof 35 is. Je wilt met een
kwast een verflaag van 70 micrometer dikte aanbrengen. |
| |
|
|
|
| |
a. |
Bereken hoeveel vierkante meter je met zo’n blik verf
maximaal kunt schilderen. |
| |
|
|
|
| |
Iemand heeft 15 liter verf gekocht met
een percentage vaste stof van 67. Hij gaat een verflaag van 60
micrometer dikte aanbrengen. Met deze gegevens ingevuld, luidt de
formule dan: |
| |
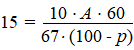 |
| |
|
|
|
| |
In deze formule is te
zien dat de oppervlakte A die hij met deze hoeveelheid kan verven nu
alleen nog afhangt van het verliespercentage p. Het verband tussen A en p
is lineair. Bovenstaande formule is dus te herschrijven tot een formule
van de vorm A = a • p + b. |
| |
|
|
|
| |
b. |
Bereken a en b. |
| |
|
|
|
| |
|
|
|
| 2. |
De hoeveelheid van een
geneesmiddel dat een kind per dag krijgt toegediend is kleiner dan die
voor volwassenen.
Uiteraard hangt die hoeveelheid ook nog af van het lichaamgewicht van
het kind.
Een apotheker gebruikt het model: K = 0,04 • V • G •
(L + 1)
Daarin is K de hoeveelheid voor een kind (in mg), V de
doseringsfactor voor een volwassene (aantal mg per kg lichaamsgewicht),
G het gewicht van het kind (in kg), en L de leeftijd in jaren. |
| |
|
|
|
| |
a. |
Een kind van 5 jaar
is 12 kg zwaar en krijgt volgens deze formule van een bepaald
geneesmiddel 100 mg toegediend.
Hoeveel zou een volwassene van 68 kg van dit middel moeten krijgen? Rond
af op honderden milligrammen |
| |
|
|
|
| |
b. |
Op welke leeftijd is iemand
volgens deze formule volwassen? |
| |
|
|
|
| 3. |
De tevredenheid T
(uitgedrukt in een getal tussen 0 en 100) die iemand in zijn beroep
ervaart blijkt afhankelijk te zijn van twee dingen. Op de eerste plaats
van het mandsalaris S (in euro)
Op de tweede plaats van de werkdruk W, dat is het percentage van de
werktijd dat iemand geconcentreerd moet zijn.
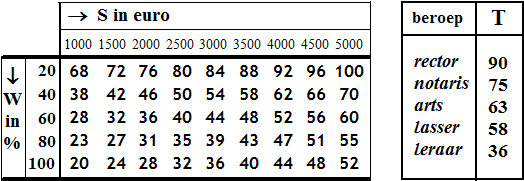
De tabel linksonder laat zien hoe T van W en S afhangt. Zo zie je
bijvoorbeeld dat iemand die 60% van de tijd geconcentreerd moet zijn en
een maandsalaris van 3500 euro heeft, een tevredenheid van 48 zal
hebben.
De tabel rechtsonder geeft de tevredenheid van zes geïnterviewde
personen. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
De volgende formule
blijkt te gelden: T = 0,008 • S + 1200/W |
| |
|
|
|
| |
a. |
De leraar heeft een
werkdruk van 94%. Hoe groot is zijn maandsalaris? |
| |
|
|
|
| |
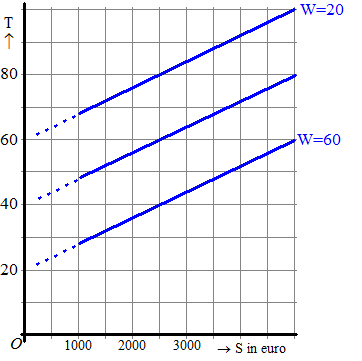
Hiernaast zie je voor
een aantal waarden van W de grafiek van T(S) getekend. |
 |
| |
|
|
| |
b. |
Bij de middelste grafiek hoort
niet W = 40.
Welke waarde van W hoort wél bij de middelste grafiek? |
| |
|
|
| |
Om burn-out te
voorkomen moet de tevredenheid eigenlijk boven de 40 liggen. Een
bedrijf stelt daarom als regel dat het salaris van iemand 50 keer zo
hoog als zijn werkdruk is. |
| |
|
|
| |
c. |
Stel een formule op voor T(W) en
laat daarmee zien dat deze maatregel inderdaad alle burn-out voorkomt! |
| |
|
|
|
| 4. |
Een school stelt een
studie-uur in de kantine in, waarin erg veel leerlingen tegelijk aan het
werk zijn. Het blijkt echter maar matig te lopen omdat alle leerlingen
nogal dicht op elkaar zitten en elkaar storen. Men stelt het volgende
model op: E = 3L - 60/(2 + 2S)
Daarin is:
E = effectieve werktijd: het aantal minuten van het uur dat
werkelijk aan schoolwerk wordt besteed
L = leeftijd in jaren
S = afstand tot de dichtstbijzijnde andere leerling in meters. |
| |
|
|
|
| |
a. |
Twee leerlingen van
15 jaar zitten 1 meter uit elkaar. Hoeveel procent zal hun effectieve
werktijd verbeteren als ze een meter verder uit elkaar gaan zitten? |
| |
|
|
|
| |
b. |
Een leerlinge van 15
jaar besteedt slechts 23 minuten van het uur effectief. Bereken hoe
dicht de dichtstbijzijnde leerling zit. |
| |
|
|
|
| |
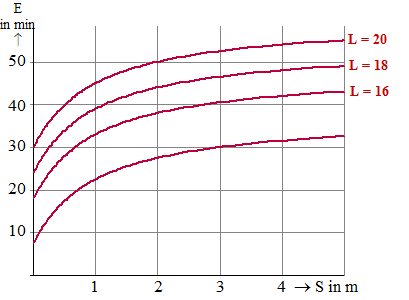
Hiernaast zie je een
grafiekenbundel die deze formule weergeeft. |
 |
| |
|
|
| |
c. |
Welke waarde van L hoort bij de
onderste grafiek? |
| |
|
|
| |
d. |
Hoe ver zouden de 16-jarigen uit
elkaar moeten zitten om even effectief te werken als de 20-jarigen met
afstand 50 cm? Beantwoord je vraag met de grafiek. |
| |
|
|
| |
Na een paar maanden
grijpt de schoolleiding eindelijk in. Men besluit de onderlinge afstand
van alle leerlingen verplicht gelijk te maken aan 1,5 meter. |
| |
|
|
|
| |
e. |
Geef een vergelijking
van het lineaire verband dat dan geldt tussen E en L. |
| |
|
|
|
| 5. |
Examenopgave HAVO
Wiskunde A, 2023-I
De uitgaven aan
huisartsenzorg voor één persoon per jaar kan je volgens een eenvoudig
model berekenen met de volgende formule:
U = 60 + 10
· A
Hierin is U het bedrag in euro dat voor één persoon per jaar aan
huisartsenzorg wordt uitgegeven en A het aantal huisartsconsulten
van die persoon per jaar.
Voor ouderen is het aantal huisartsconsulten per persoon per jaar hoger
dan voor jongeren. Voor personen van 5 jaar tot en met 64 jaar geldt
voor het aantal huisartsconsulten per persoon per jaar A de
volgende formule:
A = 1,75 + 0,05
· l
Door deze formules te combineren kan voor personen van 5 jaar tot en met 64 jaar een
formule worden afgeleid waarin de uitgaven aan huisartsenzorg per
persoon per jaar (U) worden uitgedrukt in de leeftijd (l)
van de persoon.
Deze formule kan worden geschreven in de vorm U = ...
· l + ... waarbij op de
puntjes getallen staan.
Geef de afleiding
van de formule in deze vorm. |
| |
|
|
|
| |
|
|
 |
|
© h.hofstede (h.hofstede@hogeland.nl)
|