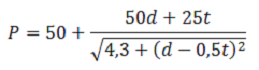Functies van meer variabelen.

© h.hofstede (h.hofstede@hogeland.nl)

   
Tot nu toe was een functie steeds een "machientje" waar je een getal (meestal x) instopte en waar dan een nieuw getal (y) uitrolde. We schreven  y = ......  of  f(x) = .......   waarbij op die stippeltjes dan de één of andere formule met x-en stond. 
   
Deze les stappen we over naar functies van meer variabelen; dat betekent:  machientjes waar méér dan één letter in moet.
Hiernaast zie je schematisch het verschil tussen een functie van één variabele en een functie van twee variabelen.

Het enige verschil is eigenlijk dat er bij functies van twee variabelen een formule hoort met twee letters achter het = teken.

Nou ja enige....

Dat heeft nogal gevolgen!

Grafieken.
Het eerste nogal vervelende gevolg is, dat we niet gewoon een grafiek van een functie van twee variabelen kunnen tekenen.
Bij één variabele hadden we voor de x de x-as en voor f(x) de y-as. Maar nu kan dat niet meer! Voor de invoer hebben we al twee assen nodig, dus voor de f(x, y) zouden we een derde as nodig hebben. Dat zou een ruimtelijke grafiek opleveren, en die zijn nogal lastig te tekenen, en ook lastig af te lezen.
En dan hebben we het nog niet eens over functies van 3, 4, ... variabelen. Dat zou een 4D, 5D,... grafiek vereisen!!!

Vergelijkingen
Een tweede ook vervelend gevolg is, dat vergelijkingen f(x, y) = ....   meestal niet meer één oplossing hebben, of twee of drie of zo. Nee, meestal zijn er nu oneindig veel oplossingen!  Allemaal paren (x, y) die aan de vergelijking voldoen.

Moeilijkheden, moeilijkheden, moeilijkheden!
Laten we ons daarom eerst maar eens beperken tot functies van twee variabelen.
   
Functies van twee variabelen.
   
Als voorbeeld neem ik een erg actuele functie:  die van de BMI.
BMI staat voor "Body-Mass-Index" en het is een getal dat aangeeft of je te dik of juist te mager bent. Een mooie BMI-meter staat op deze site van de hartstichting. Hiernaast zie je wat de BMI waarden betekenen voor je gezondheid.
De formule is:  BMI = G/L²  waarin G het gewicht in kilo van iemand is, en L zijn of haar lengte in meters.
Dat is dus een functie  van twee variabelen: BMI(G,L).
BMI  
< 18,5 te licht
18,5 - 25 gezond gewicht
25 - 30 licht overgewicht
> 30 te zwaar
   

   
Een grafiekenbundel maken.  
   
Om een beetje een idee van deze functie te krijgen gaan we een variabele vastzetten. Dat betekent: we kiezen er gewoon een getal voor en houden dat constant.
Neem bijv.  L = 1,8  dan wordt de formule  BMI = G/1,82 ≈ 0,31G
Neem bijv.  L = 1,9  dan wordt de formule  BMI = G/1,92 ≈ 0,28G
Neem bijv.  L = 2,0  dan wordt de formule  BMI = G/2,02 = 0,25G
enz.

Zo krijg een een hele serie formules, elk horend bij één bepaalde L (die is vastgezet). Deze formules hebben nog maar één variabele, dus die kun je makkelijk tekenen. Zet bij elke grafiek welke L erbij hoort, en je krijgt een grafiekenbundel als hiernaast.
Het gebied met een gezonde BMI is als een groene strook aangegeven.
Zo kun je bijvoorbeeld in één keer aflezen dat iemand van 1,80 meter een gewicht tussen de 60 en 80 kg moet hebben om een gezond gewicht te hebben.

   
Maar het kan natuurlijk net zo goed andersom:  je kunt ook G vastzetten.
Neem bijv.  G = 60 dan wordt de formule  BMI = 60/L²
Neem bijv.  G = 70 dan wordt de formule  BMI = 70/L²
Neem bijv.  G = 80 dan wordt de formule  BMI = 80/L²
enz.

Ook daarvan kun je een grafiekenbundel maken. Dat geeft een plaatje als hiernaast.

   
De ruimtelijke grafiek van BMI(G,L) is een combinatie van beide voorgaande plaatjes. Dat ziet er ongeveer zó uit:
   

   
Die blauwe lijnen zijn de rechte lijnen uit de eerste grafiekenbundel, en die rode lijnen zijn de krommen uit de tweede grafiekenbundel. Samen levert dat het rood-blauwe  "BMI-vlak" hierboven. (De oorsprong, waar de drie assen elkaar snijden is hier niet (0,0,0))
Maar goed eigenlijk heb je aan zo'n ruimtelijke grafiek niet zoveel.

Er is echter een derde plaatje waar je wél wat aan hebt, en dat is een zogenaamd hoogtekaartje.
Daarin is de BMI als constante gekozen.

BMI = 18,5 geeft  18,5 = G/L² ofwel  G = 18,5L2
BMI = 25 geeft  25 = G/L² ofwel  G = 25L2
BMI = 30 geeft  30 = G/L² ofwel  G = 30L2
En dat geeft het kaartje hiernaast.

De lijnen van constante BMI heten ook wel hoogtelijnen. Het zijn immers de lijnen in de ruimtelijke grafiek van punten die op dezelfde (BMI) hoogte liggen.
Het voordeel van dit kaartje is, dat je bij een bepaalde lengte en gewicht direct kunt zien of je gewicht gezond is (in het groene gebied valt) of niet.

   
Functies van meer variabelen.

Nou, weinig nieuws onder de zon. Het werkt eigenlijk precies zoals hierboven. Je zet alle variabelen op één na vast, en dan kun je daarvan weer een grafiekenbundel maken. Of je zet ze op twee na vast en je maakt een hoogtekaartje.

   
   
  OPGAVEN
   
1. Na een uitgebreid onderzoek onder middelbare scholieren blijkt er een verband te bestaan tussen het cijfer (C) dat een leerling op een toets haalt, het IQ (I)  van de leerling en de tijd (t) die de leerling aan de voorbereiding besteedde. Men ontwikkelt de volgende formule:
       
 

       
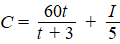  Daarbij staat C = 100 voor een 10,0 en is t de tijd in uren gemeten.
       
  a. Marion beweerde na de toets trots:  "Ik had er 6 uur op geleerd en heb toch maar mooi een 6,4 gehaald"
Hoe hoog is dan het IQ van Marion?
     

120
  b. Hoe lang moet iemand met een IQ van 80 leren om een 5,5 te halen?  Wat kan hij of zij maximaal halen?
     

5,57 uur ,een 7,6
  c. Teken een grafiekenbundel voor t = 2, 3 en 5. 
Kleur daarin het gebied waarvoor geldt:   C < I  en  I < 120 en 2 < t < 5
       
  d. Uiteraard kan iemand nooit meer dan een 10,0 halen. Voor welke waarden van  I  kan deze formule daarom niet geldig zijn?
     

I > 200
       
2. examenvraagstuk HAVO.

Het drinken van alcoholische consumpties beïnvloedt de rijvaardigheid negatief. Het is in Nederland dan ook verboden om met een alcoholgehalte van meer dan 0,05 een auto te besturen. Dit alcoholgehalte heet het bloedalcoholgehalte, afgekort BAG. Het BAG is afhankelijk van verschillende factoren:
       
  -
-
-
-		 de hoeveelheid alcohol die je drinkt;
je gewicht;
of je een man of een vrouw bent;
de tijd die verstreken is na de laatste alcoholconsumptie.
       
  Er zijn formules opgesteld waarmee je vrij nauwkeurig kunt berekenen wat je BAG is. Voor mannen en vrouwen zijn de formules dus verschillend:
BAGman = 0,01241• h • p • m −1 − 0,017 • t
BAGvrouw = 0,01535 • h • p • m −1 − 0,016 • t
       
 

Hierin is:
h de hoeveelheid alcoholische drank in cl (centiliter)
m het lichaamsgewicht in kg
t de tijd in uren na de laatste alcoholconsumptie

Als er geen alcohol in het bloed zit, is het BAG nul. Een man van 79 kg drinkt op een avond 3 flesjes bier van elk 30 cl, met een alcoholpercentage van 5% (dus p = 5).
       
  a. Toon aan dat er ongeveer 4 uur en 10 minuten na de laatste alcoholconsumptie geen alcohol meer in zijn bloed zit.
       
  Een man en een vrouw hebben tijdens een etentje samen een fles rode wijn van 75 cl leeggedronken. Die wijn bevatte 12,5% alcohol. De man van 85 kg heeft uiteindelijk 45 cl van de wijn op en de vrouw van 68 kg 30 cl. Ze dronken tegelijk hun laatste slok wijn op.
Na deze laatste slok willen ze zo snel mogelijk naar huis. Ze willen hierbij niet het verbod overtreden om een auto te besturen met een BAG van meer dan 0,05.
       
  b. Wie mag als eerste de auto besturen? Licht je antwoord toe.
     

de man
  In de rest van de opgave gaan we uit van mannen die direct na de laatste alcoholconsumptie (willen) autorijden. De formule wordt dan:

BAGman = 0,01241 • h • p •m−1

Een jonge man wil weten hoeveel hij kan drinken om meteen daarna nog steeds te mogen autorijden zonder het verbod te overtreden. De man weegt 83 kg en drinkt flesjes bier met een alcoholpercentage van 5. In een flesje zit 30 cl bier.
       
  c. Hoeveel flesjes bier mag de man dan volgens de wettelijke norm maximaal drinken? Licht je antwoord toe.
     

2,2 flesjes
       
3. examenvraagstuk HAVO Wiskunde A, 2009  (uitgebreid)

Verf is een bijzondere stof. Wanneer je het aanbrengt, is het vloeibaar, na het drogen is het hard. Verf bestaat namelijk uit vaste stof die opgelost is in een vloeistof die tijdens het drogen verdampt.

We noemen het aantal vierkante meters dat met een liter verf geschilderd kan worden het rendement. Het rendement kun je berekenen met de formule:
       
   

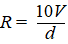  Hierin is:
− R het rendement (in m2/liter);
− V het percentage vaste stof van de verf;
− d de dikte van de verflaag (in micrometer (1 micrometer is 0,001 millimeter)).

Op een blik verf staat vermeld dat het percentage vaste stof 67 is en dat het rendement 12 m2/liter is.
       
  a. Bereken de dikte van de verflaag in micrometer waar de fabrikant blijkbaar van uitgegaan is.
       
  Verf van topmerken is per liter duurder dan verf van huismerken van doe-het-zelfzaken. Maar verf van huismerken bevat meestal een kleiner percentage vaste stof dan verf van topmerken. Om te weten welke verf het goedkoopste is, moet je dus niet kijken naar de prijs per liter, maar naar de prijs per vierkante meter aangebrachte verf.

Een huismerkverf kost 21 euro per liter en heeft een percentage vaste stof van 30. Verf van een topmerk kost 25 euro per liter en heeft een percentage vaste stof van 40. We vergelijken van beide merken een verflaag van 50 micrometer dikte.
       
  b. Onderzoek welke verf het goedkoopste is.
       
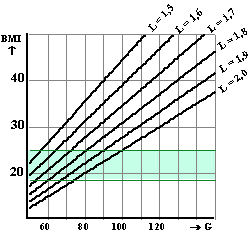
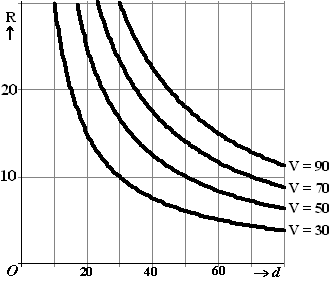
  Hieronder staat een grafiekenbundel voor de dikte en het rendement bij een aantal waarden van  het percentage vaste stof.
       
   

     
  c. Teken ook zo goed mogelijk de lijn voor V = 10 in deze grafiek.
       
  d. Arceer het gebied waarvoor het vaste stof percentage groter dan 30 is, en de dikte groter dan 20 micrometer en het rendement minder dan 20 m2/liter.
       
4. Een eigenaar van een spellenwinkel  houdt goed bij hoeveel  hij verkoopt in een week.
Dat aantal spellen (N)  blijkt af te hangen van twee dingen, namelijk van de prijs (P, in euro) die hij per spel vraagt en ten tweede van het bedrag dat hij aan reclame besteedt  (R, in euro per week).
Hij vindt het volgende verband:   N = 150 - 10P + 0,4R
       
  a. Teken een grafiekenbundel voor N = 40, 60, 80, 100.
Beperk je daarbij tot het gebied  8 < P < 14  en   0 < R < 100.
       
  b. De eigenaar besluit  €50,- uit te geven aan reclame.
Hoe moet hij dan de verkoopprijs P kiezen om 60 spellen per week te verkopen?
     

P = 11
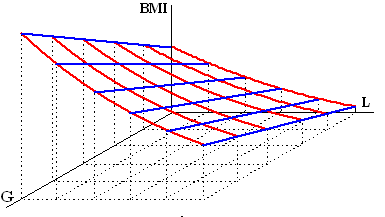
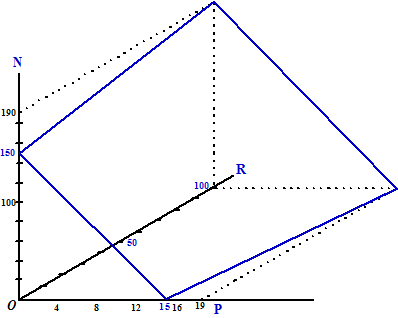
  c. Hieronder zie je een ruimtelijke grafiek van N(P, R)
Leg duidelijk uit waar je de getallen 0,4 en -10 uit de formule kunt terugvinden in deze grafiek.
       
 

       
  d. Arceer het gedeelte van deze grafiek waar geldt dat de eigenaar meer dan €50 aan reclame uitgeeft.
       
5. Examenvraagstuk HAVO-A 1989-I.

In de tijd rond Koninginnedag worden er in veel gemeenten in Nederland kermissen georganiseerd. Een kermisexploitant die een plaats wil hebben op de kermis moet staangeld aan de gemeente betalen. Dat staangeld wordt berekend naar het elektriciteitsverbruik en de oppervlakte van die plaats.
In onderstaande tabel staan van 6 kermisattracties de oppervlakte en het elektriciteitsverbruik vermeld.
       
 
  Attractie Oppervlakte
(in m2)		 Elektriciteitsverbruik
per dag (in kWh).

1
2
3
4
5
6

 Reuzenrad
Surfer
Spookhuis
Draaimolen
Breakdance
Vliegend Tapijt		 320 
300
350
230
450
300		 400
350
300
300
500
450
       
  Een gemeente rekent €5,00 huur per m2 grond per dag en €0,25 per kilowattuur (kWh)
       
  a. Bereken voor de attracties uit de tabel het staangeld in euro's per dag.
       
  Stel:  
O = de oppervlakte die de attractie in beslag neemt (in m2 )
E = het elektriciteitsverbruik van een attractie per dag (in kWh)
S = het staangeld voor een attractie per dag (in euro) 
       
  b. Stel een formule op voor S uitgedrukt in O en E.
       
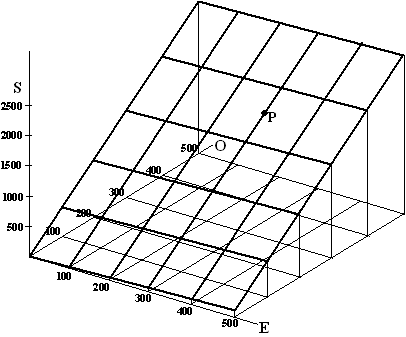
  Bij de formule uit de vorige vraag hoort de volgende grafiek:
       
 

       
  c. Welke attractie hoort bij punt P?  
       
  Bij de vaststelling van het staangeld worden door de gemeente ook nog kosten voor reinigingswerkzaamheden in rekening gebracht. Die kosten bedragen €50,- per attractie per dag.
       
  d. Geef een nieuwe formule die S uitdrukt in O en E. Leg duidelijk uit hoe de grafiek hierboven moet worden aangepast.
       
6. Examenvraagstuk HAVO-A, 1995-II

De woningen in een flatgebouw worden centraal verwarmd. Jaarlijks moeten de bewoners de verwarmingskosten gezamenlijk betalen. In verband hiermee wordt met metertjes op de radiatoren per woning geregistreerd hoeveel warmte-eenheden zijn verbruikt. Bij de jaarlijkse afrekening let men ook op het vloeroppervlak van elke woning; de woningen zijn niet allemaal even groot.

In een zeker jaar zijn de kosten:
   Totale energiekosten TE (kosten van het gas)  €37760,-
   Overige kosten OV (onderhoud en afschrijving)  €3810,-
In alle woningen samen zijn 2360 warmte-eenheden verbruikt. Het vloeroppervlak van alle woningen samen is 5936 m2. De kosten worden op een speciale manier aan de bewoners doorberekend:
• 70% van de totale energiekosten wordt verdeeld over de verbruikte warmte-eenheden
• de rest van de totale energiekosten en de overige kosten worden verdeeld op basis van het vloeroppervlak van de woningen.
       
  a. Toon aan dat de kosten per verbruikte warmte-eenheid €11,20 en de kosten per m2 vloeroppervlak €2,55 bedragen.
       
  Een bewoner met een flat waarin W warmte-eenheden verbruikt worden en waarvan de vloeroppervlakte V m2 is, zal zijn verwarmingskosten K met behulp van de volgende formule kunnen berekenen:
K = 11,20W + 2,55V    (formule 1)

Er komt een voorstel van de flatbewoners om dat jaar niet 70% van de totale energiekosten TE over de verbruikte warmte-eenheden te verdelen, maar 90%. De overige 10% van de totale energiekosten zullen dan, samen met de overige kosten OV, naar vloeroppervlak verdeeld worden. Formule 1 zal dan aangepast worden.
       
  b. Maak een bijbehorende nieuwe formule. Licht je antwoord toe.
       
  De formule van vraag 2 noemen we formule 2. Formule 2 betekent niet voor iedere bewoner een verandering in de verwarmingskosten K. Als de formules 1 en 2 dezelfde uitkomst geven, bestaat tussen W en V het volgende verband:  V = 2,52W.
     

  c. Toon dit aan.
     
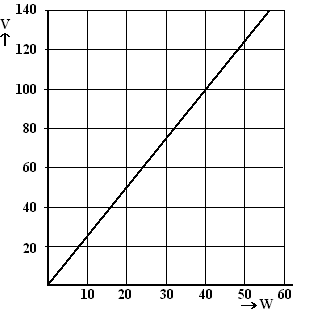
  In de figuur hiernaast is de grafiek van V = 2,52W getekend. De woningen variëren in vloeroppervlakte van 90 m2 tot 115 m2 .  De hoeveelheden verbruikte warmte-eenheden lopen van 30 tot 55. We kijken naar de situaties waarin met de nieuwe formule 2 lagere verwarmingskosten moeten worden betaald dan met formule 1. 
     
  d. Arceer in de figuur hiernaast het gebied met deze situaties. Licht je werkwijze toe.
       
7. Examenvraagstuk HAVO-A, 1994-II

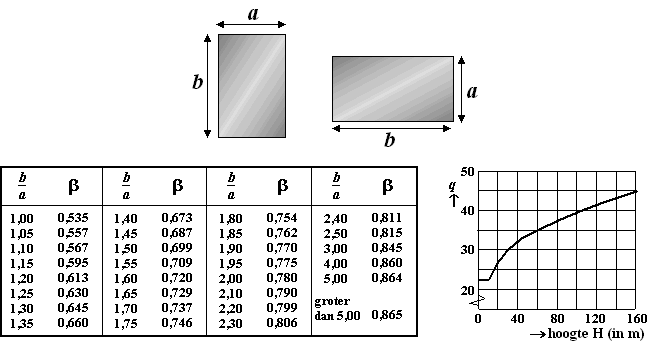
In huizen en gebouwen wordt voor grote ruiten dikker glas gebruikt dan voor kleine ruiten. Dat is nodig om de ruit voldoende stevigheid te geven. De benodigde dikte wordt echter niet alleen bepaald door de dikte van een ruit. Om de minimaal benodigde dikte D van een ruit te bepalen gebruikt men de volgende formule:  
D = 0,447 × b × a × q
In de formule en het vervolg van deze opgave worden de volgende symbolen gebruikt:
• D = minimale dikte in mm
• a = kleinste zijde van de ruit in m.
• b = grootste zijde van de ruit in m.
• b = vormfactor, afhankelijk van b/a.
• q = windbelastingsfactor
• H = hoogte waar de ruiten in het gebouw zitten in m.
       

       
  In een hoog kantoorgebouw hebben alle ruiten dezelfde afmetingen:  a = 2 en b = 3.
       
  a. Laat zien dat de minimale glasdikte voor ruiten op 5 m hoogte ongeveer 14 mm is.
       
  b. Hoeveel procent moeten de ruiten op 60 m hoogte dikker zijn dan de ruiten op 5 m hoogte? Licht je antwoord toe.
     

56%
  Stel dat de lengte en breedte van de ruiten op 100 m hoogte nog mogen variëren. De oppervlakte van de ruit moet wel 6 m2 zijn en de kleinste zijde a moet minstens 1 m zijn.
       
  c. Onderzoek of de minimale dikte het kleinst is als de ruit vierkant is.
       
  d. In een gebouw wil men op 100 m hoogte ruiten plaatsen waarvan de verhouding van lengte en breedte 8 : 5 is. De dikte van de ruiten moet 22 mm zijn. Welke afmetingen kunnen de ruiten maximaal hebben? Licht je antwoord toe.
       
8. Met de verzendservice UPS kun je pakketten versturen. De prijs die men daarvoor vraagt hangt af van het gewicht van het pakket en van de afstand waarover het moet worden verstuurd volgens de formule:
P = 2,20 + 0,12G + 0,04A
Daarin is P de prijs in euro, G het gewicht in kg en A de afstand in km.
       
  a. Iemand heeft voor  €16,80 een pakket over een afstand van 100 km verzonden. Hoe zwaar was dat pakket?
     

88,33 kg
  b. Teken een grafiekenbundel met op de x-as de afstand en op de y-as het gewicht.
       
  c. Een klant twijfelt erover of hij één of twee dezelfde pakketten moet versturen.
Hij berekent dat twee pakketten versturen 9,- duurder is dan één (naar hetzelfde adres)
Over welke afstand worden die pakketten verstuurd?
     

170 km
   
9. De longinhoud (I, in liters) van een volwassene (vanaf 25 jaar) hangt van ruwweg 3 dingen af.
Ten eerste is het van belang of het om een man of een vrouw gaat.
Verder hebben de leeftijd (J, in jaren) en de lengte (L in m) invloed op de longinhoud.
De volgende twee formules blijken die longinhoud goed te benaderen
       
  vrouwen:  IV  = 1,15 • (4,43 • L - 0,026 • J - 2,89)
mannen :   IM = 1,10 • (5,76 • L - 0,026 • J - 4,34)
       
  a. Bereken de longinhoud van een man van 1,86 m lang en 50 jaar oud.
     

5,58 liter
  b. Een vrouw van 35 jaar oud heeft een longinhoud van 4 liter. Bereken haar lengte.
     

1,64 m
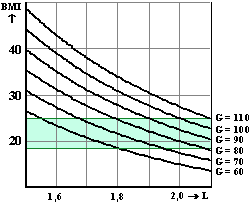
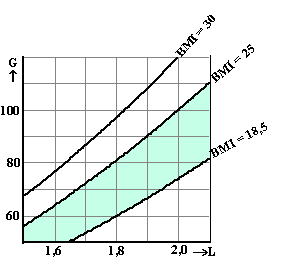
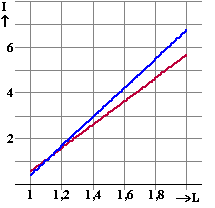
  Voor mensen van 40 jaar gelden de twee grafieken hiernaast.

     
  c. Leg uit welke grafiek bij de mannen hoort en welke bij de vrouwen.
     
  d. Leg uit hoe je die leeftijd van ongeveer 40 jaar zelf ook uit deze twee grafieken had kunnen afleiden.
     
  e. Bereken algebraïsch bij welke lengte mannen en vrouwen van 40 jaar dezelfde longinhoud hebben.
     

1,13 m
       
10. examenvraagstuk VWO Wiskunde A, 1991.

Als het gezicht van een mens bij strenge vorst ook nog aan harde wind wordt blootgesteld, kan bijzonder snel bevriezing optreden. De Amerikanen Siple en Passel behoorden rond 1940 tot de eerste wetenschappers die in Antarctica onderzoek deden naar het verband tussen het warmteverlies H van de huid, de windsnelheid w en de temperatuur T. Op grond van hun eerste metingen bij betrekkelijk lage windsnelheden stelden zij aanvankelijk een model op waarin het verband tussen H, w en T in Antarctica beschreven werd met de formule:

H = (4,2 + 4√w - 0,4w) • (33 - T)

Hierbij wordt w uitgedrukt in meters per seconde, T in graden Celsius en H in Joules per cm2 onbedekte huid per uur.
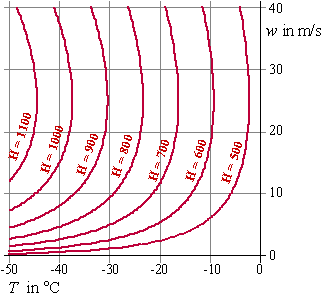
Op grond van dit model is onderstaande figuur getekend. Hierin is voor Antarctische temperaturen (T = -50 tot T  = 0) en windsnelheden tot 40 m/s een aantal iso-H-lijnen getekend.
       
 

       
  Op een onderzoeksstation in Antarctica wordt het werken in de buitenlucht gestaakt als H de waarde 800 overschrijdt. Volgens de figuur hierboven is dat bijvoorbeeld het geval bij een temperatuur van -30ºC en een windsnelheid van ongeveer 10 m/s.
       
  a. Bereken met de formule in gehele graden nauwkeurig de laagste temperatuur waarbij nog in de buitenlucht gewerkt mag worden bij een windsnelheid van 15 m/s.
     

-25 ˚C
  Uit de figuur volgt dat voor T = -20 de maximale waarde van H ligt tussen 700 en 800.
       
  b. Bereken met behulp van differentiëren hoe groot de maximale waarde van H volgens dit model is bij deze waarde van T.
     

752,6
  Omdat het aanvankelijke model van Siple en Passel niet voor alle weersomstandigheden klopt met de realiteit in Antarctica, was een bijstelling van het model nodig.
Bij verder experimenteren ontdekten ze dat het aanvankelijke model wel klopte zolang de windsnelheid niet groter was dan 20 m/s. Als de windsnelheid vanaf 20 m/s nog verder toenam bleek H, mits de temperatuur gelijk bleef, niet meer te veranderen.
Met deze ontdekking stelden ze hun model bij.
       
  c. Leg met een figuur uit hoe de iso-H-lijnen volgens het bijgestelde model moeten lopen. Kies daarbij de assen op dezelfde wijze als in bovenstaande figuur. Het tekenen van een tweetal iso-H-lijnen is voldoende.
       
  d. Stel een formule op waarmee H in het bijgestelde model berekend kan worden bij windsnelheden van 20 m/s en hoger.
       
11. Examenvraagstuk HAVO Wiskunde B, 2005

Als er een nieuwe verkeersweg geopend wordt, dan zullen sommige automobilisten overstappen van hun gebruikelijke route naar deze nieuwe weg. Bij de planning van nieuwe verkeerswegen is het van belang te weten hoeveel procent van de automobilisten gebruik zal gaan maken van zo'n weg. 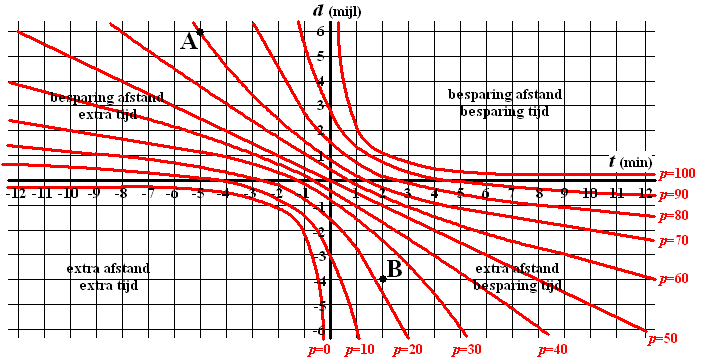Uit een onderzoek door Amerikaanse verkeersdeskundigen blijkt dat dit percentage (p) afhangt van de tijdwinst in minuten (t) en de afstandsbesparing in mijlen (d) die een nieuwe autoweg oplevert. In onderstaande figuur is voor een aantal waarden van p in grafieken weergegeven welke waarden van d en t hierbij horen. Een negatieve waarde van d of t betekent dat er sprake is van een omweg of tijdverlies.
       

       
  In deze figuur is een punt A getekend. In dit punt A geldt: p = 70,  d = 6 en t = -5.
Dit betekent dat 70% van de automobilisten gebruik zal maken van de nieuwe weg dankzij de afstandsbesparing van 6 mijl en ondanks het tijdverlies van 5 minuten.

Bij de planning van een nieuwe weg kan er gekozen worden uit twee verschillende trajecten. Traject I levert een tijdsbesparing van 4 minuten op,  maar wel een omweg van 2 mijl. Bij traject II is er een tijdverlies van 6 minuten maar een afstandsbesparing van 2 mijl.
       
  a. Onderzoek met behulp van de figuur bij welk traject (I of II) het percentage gebruikers het grootst is.
       
  Bij de grafieken uit de figuur hierboven hebben de Amerikaanse deskundigen de volgende formule gevonden voor het verband tussen p, d en t:
 

       
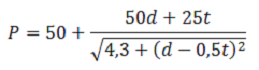
  In de figuur hierboven is tevens een punt B getekend.
       
  b. Bereken met behulp van de gegeven formule het bij punt B behorende percentage p.
       
  c. Bereken met behulp van de gegeven formule bij welke tijdsbesparing 45% van de automobilisten een omweg van 5 mijl zal accepteren.
       
  In de figuur lijkt de grafiek die hoort bij p = 50 op een rechte lijn.
       
  d. Toon op algebraïsche wijze aan dat volgens de formule deze grafiek een rechte lijn is.
       
       
© h.hofstede (h.hofstede@hogeland.nl)