|
|||||
| 1. | a. | x = cos6t x ' = 6cos5t • -sint y = sin6t y ' = 6sin5t • cost |
|||
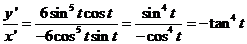 |
|||||
| b. | -tan4 t
= -9 tan4t = 9 tant = 91/4 = √3 t = 1/3π ∨ t = 11/3π naar die laatste valt af, want t moet tussen 0 en 1/2π t = 1/3π geeft x = cos6t = (1/2)6 = 1/64 en y = sin6t = (1/2√3)6 = 27/64 dus P = (1/64, 27/64) |
||||
| 2a. | x = 0
geeft
2sin2t = 0 sin2t = 0 2t = 0 + k2π ∨ 2t = π + k2π t = 0 ∨ t = 1/2π + kπ t = 0 is de oorsprong, t = 1/2π en t = -1/2π zijn de gezochte punten. t = 1/2π geeft y = 3/4π2 x ' = 4cos(2t) dus x'(±1/2π) = -4 y' = 6t dus y'(±1/2π) = ±3π De helling van kromme K is gelijk aan y'/x' = ±3/4π De lijn y = -3/4πx + 3/4π2 snijdt de x-as als -3/4πx + 3/4π2 = 0 πx = π2 x = π De basis van de driehoek heeft dus breedte 2π, en de hoogte is 3/4π2 De oppervlakte is dan 3/4π3 |
||||
| 2b. | y = p
geeft twee waarden van t die elkaars tegengestelde zijn. Dan is AB = 2sin(2t) - 2sin(-2t) = 2 sin(2t) - sin(-2t) = 1 2sin(2t) = 1 sin(2t) = 1/2 2t = 1/6π + k2π ∨ 2t = 5/6π + k2π t = 1/12π + kπ ∨ t = 5/12π + kπ Dan is y = 3/144π2 of y = 75/144π2 |
||||
| 3. | a. | sint • cost = 1/4 1/2sin(2t) = 1/4 sin(2t) = 1/2 2t = 1/6π + k2π ∨ 2t = 5/6π + k2π t = 1/12π + kπ ∨ t = 5/12π + kπ tussen 0 en 2π zijn dat 1/12π, 5/12π, 13/12π, 17/12π. |
|||
| b. | P gaat door de oorsprong als cost = 0 Dat is bij t = 1/2π en t = 3/2π x ' = -sint y' = costcost - sintsint bij t = 1/2π geeft dat x' = -1 en y ' = -1 bij t = 3/2π geeft dat x' = 1 en y' = -1 De hoek is 90º (kun je met een schetsje snel zien) |
||||
| 4. | x
' = 3cos2t • -sint y ' = 3sin2t • cost rc = y'/x' = -sint/cost raaklijn: sin3t = -sint/cost • cos3t + b b = sint B = (0, sint) 0 = -sint/cost • x + sint x = cost dus A = (cost, 0) AB = √(sin2t + cos2t) = 1 |
||||
| 5. | a. | x
' = 2t en y ' = 1 Dus de helling van de parabool is y'/x' = 1/2t Omdat A = (a , √a) = (t2, t) is t = √a Dus de helling van de parabool in A is 1/2√a De helling van MA is (0 - √a)/(r - a) Als MA loodrecht op de parabool staat moeten de hellingen met elkaar vermenigvuldigd -1 zijn. 1/2√a • -√a/(r - a) = -1 1/2(r - a) = 1 2(r - a) = 1 r - a = 1/2 a = r - 1/2 |
|||
| b. | Noem
de projectie van A op de x-as punt P De driehoek APM heeft zijden: AP = √a PM = 0,5 (zie vorige vraag) AM = 0,5a + 0,25 (want MA = 0,5r als A het midden van MB is) In deze driehoek geldt natuurlijk Pythagoras: (0,5a + 0,25)2 = (√a)2 + 0,52 0,25a2 + 0,25a + 0,0625 = a + 0,25 0,25a2 - 0,75a - 0,1875 = 0 a2 - 3a - 0,75 = 0 a = (3 ± √12)/2 = 3/2 ± √3 a is positief dus a = 3/2 + √3 dan is r = a + 1/2 = 2 + √3 |
||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||