| |
ę h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Meer opgaven |
 |
| |
|
|
|
 |
| |
|
|
|
 |
Los algebra´sch op: |
|
| |
|
|
|
| |
a. |
x3 - 3x2
= 0 |
|
| |
|
|
|
| |
b. |
4x5 + 2x6
= 0 |
|
| |
|
|
|
| |
c. |
x7 = 4x5
|
|
| |
|
|
|
| |
d. |
x7 - 243x2
= 0 |
|
| |
|
|
|
 |
Los algebra´sch op: |
| |
|
|
|
| |
a. |
x4 + 2x2
- 15 = 0 |
|
| |
|
|
|
| |
b. |
9x2 + x4
+ 18 = 0 |
|
| |
|
|
|
| |
c. |
x4 + 14 = 9x2 |
|
| |
|
|
|
| |
d. |
3x4
- 6x2
= 144 |
|
| |
|
|
|
 |
Los algebra´sch op: |
| |
|
|
|
| |
a. |
x8 = 4x4
+ 12 |
|
| |
|
|
|
| |
b. |
3x4 + x7 =
x4 + 5x7 |
|
| |
|
|
|
| |
c. |
x2√x
- 2x√x = 24√x |
|
| |
|
|
|
| |
d. |
x8
- 5x5
+ 4x2 = 0 |
|
| |
|
|
|
| |
e. |
x7
- x5
- 6x3 = 0 |
|
| |
|
|
|
 |
Examenvraagstuk HAVO Wiskunde B,
2005. Gegeven is de functie f (x)
= -x3 + 27x + 44
Q is het snijpunt van de grafiek van f
met de y-as. De lijn k door Q evenwijdig aan de x-as
snijdt de grafiek ook nog in de punten P en R. |
| |
|
|
|
| |
a. |
Bereken de lengte van PR.
Rond je antwoord af op twee decimalen. |
| |
|
|
|
| |
Een familie van functies is gegeven door h(x)
= (x + 4)(p + 4x - x2 ), waarbij p
elk reŰel getal kan voorstellen. |
| |
|
|
|
| |
b. |
Toon aan met behulp van algebra
dat er een waarde van p is waarbij de bijbehorende functie h
gelijk is aan de functie f. |
| |
|
|
|
 |
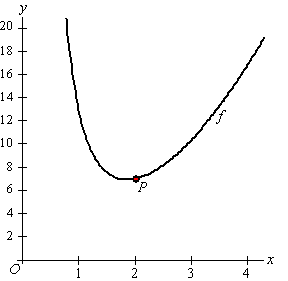
examenvraagstuk HAVO Wiskunde B,
2012. |
| |
|
|
|
| |
De functie f
is gegeven door
f (x) = x2
+ 12x -2,
met x > 0.
In de figuur hiernaast is de grafiek van
f
getekend.
Een horizontale lijn snijdt de grafiek van
f
in de punten
A
en
B.
De x-co÷rdinaat
van A
is 1.
Bereken de
x-co÷rdinaat
van B.
Geef je antwoord in twee decimalen
nauwkeurig. |
 |
| |
|
|
|
|
|
| |
|
|
|
| 6. |
Een
rechthoekige driehoek heeft schuine zijde 10 en oppervlakte 24.
Noem de lengtes van de rechthoekszijden x en y
Stel twee vergelijkingen voor x en y op en bereken
vervolgens de omtrek van de driehoek. |
| |
|
|
|
| |
|
|
 |
|
ę h.hofstede (h.hofstede@hogeland.nl)
|