| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Meer opgaven |
| |
|
|
|
 |
| |
|
|
|
| 1. |
Een aantal mensen is gevraagd hoeveel minuten ze onder de douche staan
als ze douchen. Dat leverde de volgende serie douchetijden op: |
| |
|
|
|
| |
01 12 14
05 06 06
08 23 14
06 09 10
11 11 08 06
05
02 15 16
13 12 10
10 09 11
07 08 03
05 14 18 13
10
08 08 12
14 10 05
06 06 14
13 15 12
06 08 11 11
17 |
|
| |
|
|
|
| |
Maak van deze tijden een boxplot. |
| |
|
|
|
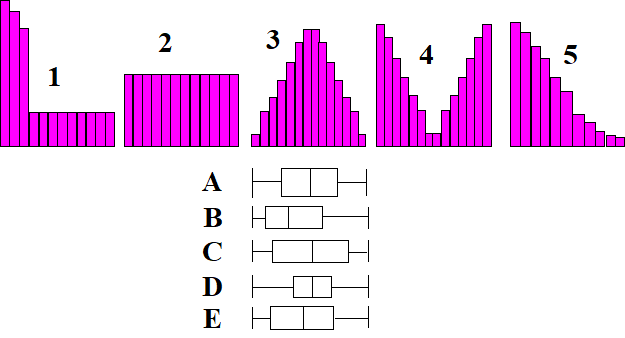
| 2. |
Hieronder staan vijf
histogrammen (1 tm 5) met daaronder vijf boxplots (A tm E). Leg uit welk histogram bij welke boxplot hoort. Doe dat zonder bij elk histogram
daadwerkelijk een boxplot te gaan tekenen. |
| |
|
|
|
| |
 |
| |
|
|
|
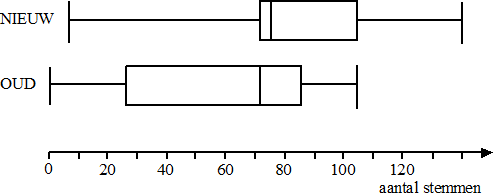
| 3. |
Voor de kerstvakantie
gaan de leerlingen van een grote scholengemeenschap zelf hun eigen
top-2000 samenstellen. Iedereen mag daarbij op 5 nummers stemmen die in
de top-2000 zouden moeten komen.
Voor de uiteindelijke top-2000 onderscheiden we OUDE nummers (die
zijn van vóór 2000) en NIEUWE nummers (vanaf 2000).
In onderstaande figuur zie je twee boxplots die het aantal stemmen op
OUDE en NIEUWE nummers aangeven. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
In totaal werden er
520 OUDE nummers en 1480 NIEUWE
nummers. |
| |
|
|
|
| |
a. |
Op welke plaats stond
het hoogst genoteerde OUDE nummer ongeveer? |
| |
|
|
|
| |
b. |
Op welke plaats
eindigde het nummer waar 65 stemmen op werden uitgebracht? |
| |
|
|
|
| |
c. |
Er was een grote
groep nummers met ongeveer het zelfde aantal stemmen. Hoeveel
stemmen hadden die nummers? |
| |
|
|
|
| |
d. |
Wat kun je zeggen
over de plaats waarop het laagst eindigende NIEUWE nummer stond? |
| |
|
|
|
| 4. |
Op de Cito-toets
kunnen kinderen een score halen tussen de 500 en de 550. Deze score
geeft aan welk type brugklas het beste geschikt is. Het advies havo komt
bijvoorbeeld overeen met een score van tussen de 538 en 541.
De rector van een grote HAVO/VWO school houdt elk jaar bij wat de
citoscores van de nieuwe eersteklassers waren.
Voor het jaar 2015 gaf dat de volgende tabel: |
| |
|
|
|
| |
| citoscore |
530 |
531 |
532 |
533 |
534 |
535 |
536 |
537 |
538 |
539 |
540 |
| frequentie |
1 |
2 |
1 |
4 |
6 |
8 |
9 |
12 |
14 |
16 |
16 |
|
| |
|
|
|
| |
| citoscore |
541 |
542 |
543 |
544 |
545 |
546 |
547 |
548 |
549 |
550 |
| frequentie |
24 |
26 |
25 |
19 |
12 |
9 |
8 |
4 |
5 |
2 |
|
| |
|
|
|
| |
a. |
Bereken de gemiddelde
citoscore van deze brugklassers. |
| |
|
|
|
| |
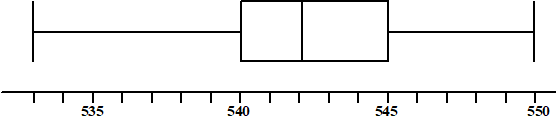
Ook in 2016 en 2017
heeft de rector de citoscores bijgehouden.
in 2016 was de gemiddelde score 540
De scores van 2017 zijn verwerkt in onderstaande boxplot. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Toon aan dat, op grond van de
boxplot, de gemiddelde citoscore in 2017 zeker hoger was dan in 2016. |
| |
|
|
 |
|
|
| |
|
|
|
| 5. |
Een pakje papieren
servetjes bevat, als je het opschrift mag geloven, 100 servetjes. In de
fabriek worden de servetjes machinaal verpakt. Daarbij vallen de
servetjes één voor één langs een lichtbundel die gekoppeld is aan een
teller. Als de teller op 100 staat wordt de stapel servetjes verpakt.
Bij dit tellen kunnen twee soorten fouten optreden:
• fout A: twee servetjes kleven aan elkaar en
worden als één servet geteld.
• fout B: een servet is verkeerd gevouwen en wordt als
twee servetten geteld.
Bij een steekproef wordt van 50 pakjes servetten het aantal met de hand
nageteld, en dat gaf de onderstaande frequentietabel: |
| |
|
|
|
| |
| aantal servetten |
95 |
96 |
97 |
98 |
99 |
100 |
101 |
102 |
103 |
| aantal keer |
1 |
2 |
4 |
6 |
9 |
14 |
9 |
3 |
2 |
|
| |
|
|
|
| |
a. |
Teken de boxplot bij deze
frequentietabel. |
| |
|
|
|
| |
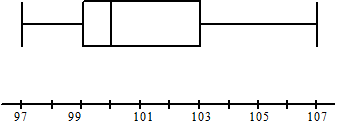
Door een aanpassing
in de verpakkingsmachine wordt bereikt dat één van beide fouten minder
optreedt. In de nieuwe situatie wordt ziet de boxplot van 50 servetten
er zó uit: |
| |
|
|
|
| |
 |
| |
|
|
|
| |
b. |
Leg uit welke van de twee
telfouten nu minder voorkomt. |
| |
|
|
|
| |
c. |
Leg uit hoe je kunt
zien dat beide telfouten nog steeds niet even vaak voorkomen. |
| |
|
|
|
| |
|
|
 |
|
© h.hofstede (h.hofstede@hogeland.nl)
|