| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
| |
|
|
|
| 1. |
Examenvraagstuk VWO Wiskunde A,
2013.
In de archeologie gebruikt men de C14-methode bij
het vaststellen van de historische leeftijd (ouderdom) van bepaalde
vondsten. Deze methode werd in 1949 ontwikkeld door de Amerikaanse
scheikundige Libby, die hiervoor de Nobelprijs gekregen heeft.
Volgens de theorie neemt de radioactiviteit van dood organisch materiaal
exponentieel af en daarom kun je door de radioactiviteit te meten
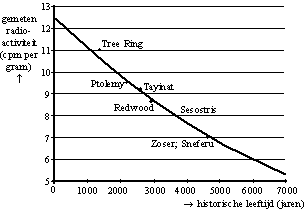
bepalen hoe oud een voorwerp is. De figuur hiernaast komt
uit een artikel van Libby uit 1949. Libby testte de C14-methode door
deze te gebruiken op zes verschillende voorwerpen waarvan de
historische leeftijd op een andere manier bekend was. |
 |
| |
|
|
|
| |
Langs de verticale as staat de gemeten
radioactiviteit in cpm (counts per minute) per gram materiaal. Dit
is een maat voor de hoeveelheid C14. Langs de horizontale as staat
de historische leeftijd van het voorwerp in jaren.
Volgens de theorie neemt de gemeten radioactiviteit
exponentieel af. De grafiek gaat door de punten (0; 12,5) en (6000;
6). Hiermee kan men de groeifactor berekenen. |
| |
|
|
|
| |
a. |
Bereken met deze punten de groeifactor per jaar in 7
decimalen nauwkeurig. |
| |
|
|
|
| |
Voor het vervolg van de opgave gaan we uit van de
formule: N = 12,5 •
0,999878t
Hierin is N de gemeten radioactiviteit van
het voorwerp in cpm per gram en t is de historische leeftijd
volgens de C14-methode van het voorwerp in jaren.
De punten in de figuur stellen de metingen aan de
voorwerpen voor. Het punt ‘Ptolemy’ hoort bij een stuk hout van een
doodskist van een Egyptische mummie. Deskundigen schatten dat deze
doodskist uit ongeveer 200 voor Chr. dateert. Voor dit hout werd in
1949 een radioactiviteit van 9,5 cpm per gram gemeten. |
| |
|
|
|
| |
b. |
Bereken het verschil tussen de historische leeftijd
volgens de C14-methode en de schatting van de deskundigen. |
| |
|
|
|
| 2. |
Examenvraagstuk HAVO Wiskunde A,
2015.
Iemand leent
bij het bedrijf Flitsmoney een bedrag van €250,00. Hij heeft dus een schuld van
€250,00. Die schuld loopt echter exponentieel op, met vaste
groeifactor. Na 30 dagen is die schuld opgelopen tot €312,50. Als je
uitgaat van exponentiële groei, kun je berekenen dat de schuld
dagelijks met ongeveer 0,75% groeit. |
| |
|
|
|
| |
a. |
Bereken dit
percentage in drie decimalen nauwkeurig. |
| |
|
|
|
| |
b. |
Zo’n
lening is duur. Een schuld die dagelijks 0,75% groter wordt,
zou na een jaar fors gegroeid zijn.
Bereken het
groeipercentage per jaar. |
| |
|
|
|
| 3. |
Examenvraagstuk VWO Wiskunde C,
2015.
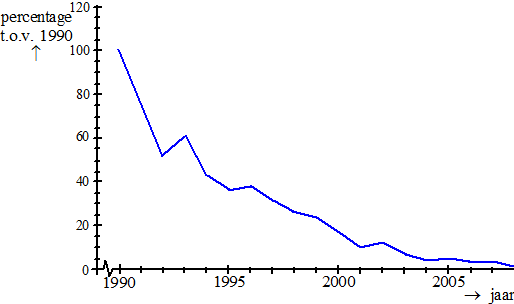
In de periode 1990
− 2005 nam het aantal kuifleeuweriken dramatisch af, zoals in de
volgende figuur goed te zien is. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
In 2005 was er nog
slechts 5% over van het aantal in 1990. Ga ervan uit dat het aantal
exponentieel afnam in deze periode. |
| |
|
|
|
| |
a. |
Bereken de
groeifactor per jaar voor de kuifleeuwerik. Ga uit van de gegevens van
1990 en 2005. |
| |
|
|
|
| |
Uit het onderzoek
is gebleken dat de plaats van het nest belangrijk is voor de mate van
succes van een vogelsoort. Een soort A die zijn nest in struiken maakt,
groeit exponentieel met groeifactor 1,042 per jaar. En een soort B die
in bomen nestelt, groeit exponentieel met groeifactor 1,016 per jaar.
Neem aan dat de aantallen van deze twee broedvogelsoorten op een bepaald
moment gelijk zijn. |
| |
|
|
|
| |
b. |
Bereken na hoeveel
gehele jaren het aantal vogels van soort A voor het eerst meer dan twee
keer zo groot is als dat van soort B. |
| |
|
|
|
| 4. |
Examenvraagstuk VWO Wiskunde A,
2015.
Bank A adverteert met de
volgende aanbieding: |
| |
|
1e
jaar 3,00% rente
2e jaar 3,25% rente
3e jaar 3,40% rente
4e jaar 3,55% rente
5e jaar 5,00% rente |
| |
|
|
|
| |
Wie spaargeld
inlegt bij bank A voor een periode van 5 jaar, krijgt dus het eerste
jaar 3,00% rente, het tweede jaar 3,25% en het derde jaar 3,40% en
zo verder. Neem aan dat bank B een vast rentepercentage per jaar
aanbiedt voor een periode van 5 jaar.
Iemand wil een bedrag inleggen bij een bank voor een periode van 5
jaar.
Onderzoek bij
welk vast rentepercentage per jaar van bank B hij bij beide banken
hetzelfde eindbedrag in handen krijgt. Rond je antwoord af op vier
decimalen. |
| |
|
|
|
| |
|
|
|
| 5. |
Examenvraagstuk VWO Wiskunde A,
2017-I |
| |
|
|
|
| |
Hieronder zie je een gitaar. De snaren zijn
gespannen tussen de brug en de kam. Op de hals zijn
zogenoemde frets (smalle metalen strips) te zien. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Als je een snaar aanslaat zonder op een fret te
drukken, gaat de hele snaar tussen de brug en de kam trillen. Door
een snaar tegen een fret aan te drukken, wordt de gebruikte
snaarlengte korter. Je krijgt dan een andere toon. Om de goede tonen
te krijgen, moet bij het bouwen van een gitaar de juiste plaats van
de frets berekend worden.
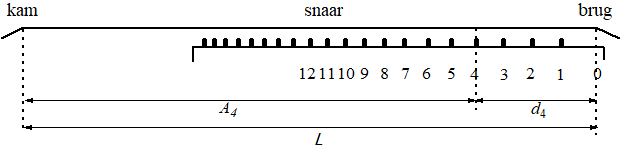
De volgende figuur geeft een schematisch zijaanzicht van de hals. De
eerste 12 frets zijn daarin vanaf de brug genummerd. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
De lengte van een snaar in cm tussen de brug en de
kam noemen we L .
An
is de afstand in cm tussen de fret met
nummer n en de kam, en
dn
is de afstand in cm tussen de fret met
nummer n en de brug.
In de figuur zijn A4 en d4
aangegeven. Voor An
geldt de volgende formule:
An = L • 0,9439n
Van een bepaalde gitaar is de afstand tussen fret
nummer 6 en de brug gelijk aan 20 cm. |
| |
|
|
|
| |
a. |
Bereken de lengte L van een snaar van deze
gitaar. Rond je antwoord af op hele cm. |
| |
|
|
|
| |
De groeifactor in de formule is berekend op basis
van de volgende uitgangspunten:
- er is een exponentieel verband tussen
An
en n;
- de 12e fret ligt precies midden tussen de brug en de
kam. |
| |
|
|
|
| |
b. |
Bereken met behulp van deze twee uitgangspunten de
groeifactor in vijf decimalen nauwkeurig. |
| |
|
|
|
| |
De theoretische formule die hiervoor
geldt, is: |
| |
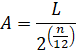 |
| |
|
|
|
| |
Deze formule kan worden herleid tot:
An
= L • 0,9439n
|
| |
|
|
|
| |
c. |
Laat deze herleiding zien. |
| |
|
|
|
| 6. |
Examenvraagstuk HAVO wiskunde
A, 2021-I |
| |
|
| |
De frequentie van een toon wordt gegeven in hertz (Hz), dit is het
aantal trillingen per seconde. Bij een hogere toon hoort een hogere
frequentie. Als je eenzelfde toon één octaaf hoger speelt, wordt de
frequentie twee keer zo groot. Er bestaat een exponentieel verband
tussen de frequenties en de tonen in de tabel: van elke volgende
toon neemt de frequentie met een vast percentage toe. In de tabel
zie je van enkele tonen de frequenties. |
| |
|
|
|
| |
| Tabel:
frequenties. |
| toon |
A |
Bes |
B |
C |
Des |
D |
Es |
E |
F |
Ges |
G |
As |
A |
| frequentie (Hz) |
440 |
|
|
|
|
|
|
|
|
|
|
|
880 |
|
| |
|
|
|
| |
Bereken op
basis van de frequenties van de A-tonen uit de tabel de frequentie
van de D-toon. Geef je antwoord in één decimaal. |
| |
|
|
|
| 7. |
Examenvraagstuk VWO Wiskunde
A, 2023-I
Traditioneel
gebrouwen whisky wordt enkele jaren in houten vaten opgeslagen om
daarin te rijpen. In het algemeen geldt: hoe langer de whisky rijpt,
hoe beter hij smaakt. Lang rijpen heeft echter een nadeel: een deel
van de whisky gaat verloren doordat deze in het houten vat trekt of
verdampt. Het deel van de whisky dat tijdens het rijpen verloren
gaat, wordt het engelendeel genoemd. Het engelendeel wordt
uitgedrukt in een percentage per jaar.
Van een bepaald soort whisky is het engelendeel 4,5%. Neem aan dat
het engelendeel elk jaar hetzelfde percentage is. |
| |
|
|
|
| |
a. |
Bereken hoelang
het duurt totdat nog maar de helft van de whisky over is. Geef je
antwoord in jaren en gehele maanden. |
| |
|
|
|
| |
In
werkelijkheid is bij traditioneel gebrouwen whisky het engelendeel
niet ieder jaar even groot. Zeker aan het begin van de
rijpingsperiode is dit deel een stuk groter, doordat de whisky nog
in het hout moet trekken.
Pappy Van Winkle 23 is een zeer exclusieve whisky die op
traditionele wijze geproduceerd wordt en, zoals de naam al
suggereert, 23 jaar in een houten vat rijpt voordat hij in flessen
gedaan wordt. Op de website van de producent staat het volgende: |
| |
|
|
|
| |
| Het rijpingsproces begint met een vat met 200 liter
whisky. Het eerste jaar gaat er maar liefst 10%
verloren, doordat de whisky in het hout trekt. De 8
jaren erna gaat er 4% per jaar verloren en daarna steeds
3% per jaar. Tenslotte gaat er van het eindproduct ook
nog 6 liter verloren bij het vullen van de flessen. |
|
| |
|
|
|
| |
Pappy Van
Winkle 23 wordt verkocht in flessen van 750 ml. |
| |
|
|
|
| |
b. |
Bereken hoeveel
van zulke flessen kunnen worden gevuld, uitgaande van 200 liter
whisky. |
| |
|
|
|
| |
|
|
 |
|
© h.hofstede (h.hofstede@hogeland.nl)
|