| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
| |
|
|
|
| 1. |
Examenvraagstuk
VWO Wiskunde B, 2002. |
| |
|
|
|
| |
Voor elke beginwaarde u0
is gegeven de rij un = -1/2 ē
(un-1)3 (voor n = 1, 2,
3, ...)
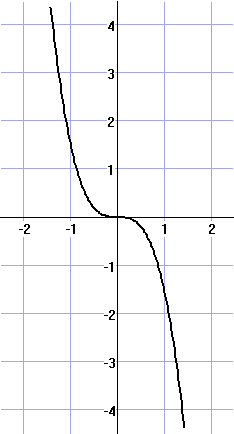
In de figuur hiernaast is de grafiek van de functie y = -1/2
ē x3 getekend.
Neem u0 = 1,5 |
 |
| |
|
|
| |
a. |
Geef in deze figuur op de x-as de
waarden u1 en u2 aan met behulp van
een webgrafiek. |
| |
|
|
| |
Of de rij u0,
u1, u2, ... naar 0 convergeert hangt
af van de beginwaarde u0. |
| |
|
|
| |
b. |
Bereken exact voor welke waarden van u0
de rij u0, u1, u2,
... naar 0 convergeert . |
| |
|
|
| |
|
|
|
| 2. |
Examenvraagstuk
VWO Wiskunde B, 2006. |
| |
|
|
|
| |
Gegeven is de functie f(x) =
√(4x
- x2 ), op het domein [0,4].
Voor startwaarden u0 tussen
0 en 8 is de rij u0, u1, u2,
... gedefinieerd door un + 1 = f (1/2un). |
.gif) |
| |
|
|
| |
a. |
Bereken u4 voor het geval dat u3
= 4/5. |
| |
|
| |
In de figuur
hiernaast zijn getekend: de
grafiek van f, de lijn y = x en de lijn y =
1/2x.
Op de x-as is een zekere startwaarde u0
aangegeven. |
| |
|
|
|
| |
b. |
Teken in deze figuur met behulp van de drie grafieken de
plaats van u2 op de x-as. |
| |
|
|
|
| |
c. |
Voor elke startwaarde u0
tussen 0 en 8 convergeert de rij u0, u1,
u2, ... naar dezelfde positieve limiet.
Bereken deze limiet op algebraÔsche wijze. |
| |
|
|
|
| |
|
|
|
| 3. |
Examenvraagstuk
VWO Wiskunde B, 2008. We beschouwen de
rij van Fibonacci: 1, 1, 2, 3, 5, 8, 13, Ö.
Deze rij wordt beschreven door de formules: |
| |
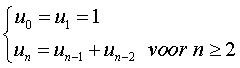 |
| |
We maken
bij de rij van Fibonacci een quotiŽntrij door elke term (behalve de
eerste) door zijn voorganger te delen: |
| |
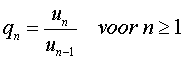 |
| |
a. |
Toon aan dat
voor elke n ≥ 2
geldt: |
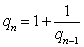 |
|
| |
|
|
|
| |
De
quotiŽntrij wordt dus beschreven door de formules |
.gif) |
| |
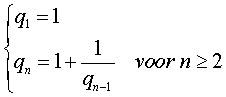 |
| |
In de
figuur hiernaast zijn de grafieken getekend van
y = 1 + 1/x
en y = x .
Verder
is op de x-as de plaats van q1
aangegeven. |
| |
|
|
| |
b. |
Geef in
deze figuur, met behulp van een webgrafiek, op de x-as
de plaats van de termen q2
, q3 en
q4 van
de quotiŽntrij aan. |
| |
|
|
|
| |
c. |
De quotiŽntrij heeft een
limiet. Bereken deze limiet exact. |
| |
|
|
|
| 4. |
Examenvraagstuk VWO
Wiskunde A,
2003.
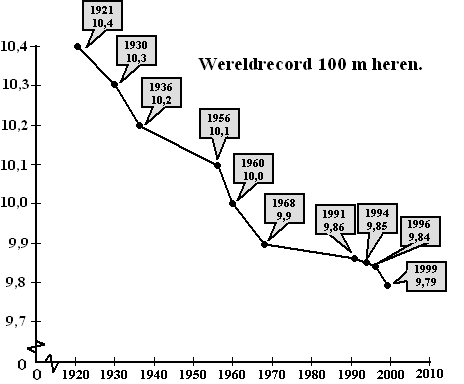
De ontwikkeling van records in de sport is
vaak onderzocht. In kranten en tijdschriften worden grafieken getoond
waarin die ontwikkeling zichtbaar wordt. In onderstaande figuur zie je
zo'n grafiek. Het gaat om de 100 meter hardlopen voor mannen. De
recordtijden zijn in seconden. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Men heeft het volgende nieuwe model
opgesteld, dat ook na 1968 redelijk goed past bij de gegevens
uit bovenstaande grafiek:
Wt = 0,9918 ē Wt
- 1 + 0,075 met W0 = 10,4Hierbij is t weer de tijd in jaren en komt t = 0
overeen met 1921.
Volgens dit nieuwe model is in 2000 het wereldrecord 9,80 seconden. |
| |
|
|
|
| |
a. |
Bereken welke recordtijd dit model
voor het jaar 2010 voorspelt. Geef je antwoord in 2 decimalen nauwkeurig. |
| |
|
|
|
| |
Volgens dit model
zullen de recordtijden steeds lager worden. Maar op den duur zullen de
records nauwelijks meer veranderen; ze naderen tot een evenwichtswaarde. |
| |
|
|
|
| |
b. |
Maak een schets van de webgrafiek bij het
nieuwe model. Leg uit hoe je in deze webgrafiek ziet dat de recordtijden
steeds lager worden en bereken de evenwichtswaarde. |
| |
|
|
|
| 5. |
Examenvraagstuk VWO
Wiskunde A, 2005. De bioloog W. Ricker heeft veel onderzoek
gedaan naar zalm in Canadese rivieren. Jaarlijkse tellingen hebben
uitgewezen dat de omvang van de zalmpopulatie sterk fluctueert. Zo komt
het voor dat de omvang van de populatie na een jaar meer dan verdubbeld
is. weer een jaar later is de omvang dan weer meer dan gehalveerd.
Ricker ontwikkelde rond 1955 een model dat goed bruikbaar is om dit
verschijnsel te beschrijven. In deze opgave bestuderen we het model:
P(t + 1) = 9 ē P(t) ē 0,99P(t)
met beginwaarde P(0)
In deze recursievergelijking is t het aantal jaren na 1984
(het tijdstip t = 0 komt dus overeen met 1 januari 1984) en is P(t)
het aantal zalmen in duizendtallen aan het begin van het betreffende jaar.
We nemen P(0) = 25. |
| |
|
|
|
| |
a. |
Bereken met hoeveel procent de
omvang van de zalmpopulatie volgens dit model is gedaald tussen begin 1986
en begin 1987. |
| |
|
|
|
| |
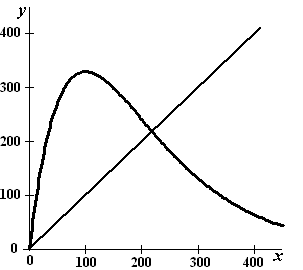
In de figuur hiernaast is de
grafiek getekend van y = 9x ē 0,99x .
Ook is de grafiek van y = x getekend.
In dengrafiek zie je dat het model twee evenwichtswaarden heeft.
Eťn ervan is P(t) = 0 |
 |
| |
|
|
| |
b. |
Bereken de tweede evenwichtswaarde |
| |
|
|
| |
Als we voor de beginwaarde de
evenwichtswaarde kiezen dan zal de rij P(0), P(1), P(2), ... steeds
dezelfde (evenwichts)waarde hebben.
Een evenwichtswaarde noemen we stabiel als bij keuzes van de
beginwaardes dicht in de buurt van de evenwichtswaarde geldt: de rij P(0),
P(1), P(2),... nadert tot die evenwichtswaarde. |
| |
|
|
|
| |
c. |
Onderzoek met een webgrafiek in
de figuur of de tweede evenwichtswaarde van het model stabiel is. |
| |
|
|
|
| |
De ontwikkeling van de populatie
volgens dit model hangt af van de beginwaarde P(0). Het is mogelijk deze
beginwaarde zo te kiezen dat dat de populatie al direct het volgende jaar
zijn maximale omvang bereikt. |
| |
|
|
|
| |
d. |
Bereken bij welke beginwaarde
dit het geval is. |
| |
|
|
|
| |
Als we weer uitgaan van 25 duizend zalmen
(dus P(0) = 25), zal het aantal zalmen een jaar later 175 duizend zijn
(dus P(1) = 175) Wanneer men in de volgende jaren telkens in het begin van
het jaar 150 duizend zalmen vangt, zal zich telkens dezelfde situatie
voordoen: het model geeft 25 duizend zalmen aan het begin van het jaar en
175 duizend zalmen aan het eind van het jaar. We zeggen daarom dat de
beginwaarde P(0) = 25 ruimt biedt om elk jaar 150 duizend zalmen te vangen
want P(1) = P(0) + 150.
Er is nog een beginwaarde die ruimte biedt om elk jaar 150 duizend zalmen
te vangen. |
| |
|
|
|
| |
e. |
Onderzoek welke andere waarde
van P(0) eveneens ruimte biedt om elk jaar 150 duizend zalmen te vangen. |
| |
|
|
|
| |
|
|
 |
|
© h.hofstede (h.hofstede@hogeland.nl)
|